При решении задач максимума и минимума функции y = f(x) одной переменной выделяют задачи локального (на каком-либо интервале) и глобального (на всей числовой оси) экстремума. В MATLAB поиск локального минимума осуществляет функция:

[х, у]= fminbnd(name, a, b [, options])

для которой:

• name - имя М-функции, вычисляющей значение f(x);
• а, b - границы интервала, на котором осуществляется поиск минимума;
• options - параметры, управляющие ходом решения;
• х, у - координаты точки, в которой достигается минимум функции на заданном интервале.

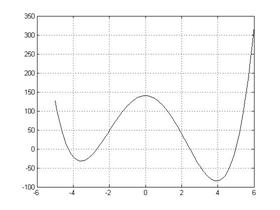
Функцию fminbnd можно использовать и для вычисления локального максимума. Для этого достаточно взять функцию name с противоположным знаком.

Пример:

В М-файле с именем mf.m пишем:

function y=mf(x)

y=x.^4-0.5*x.^3-28*x.^2+140;

end

Потом в командном окне пишем:

x=-5:0.1:6;

y=x.^4-0.5*x.^3-28*x.^2+140;

plot(x,y,'-k'), grid

%Максимум функции на интервале [-2 2]

y=-mf(x);

[x,y]=fminbnd(@mf,-2,2)

Результат:

x =

3.7224e-008

y =

-140.0000

Поиск экстремума функции нескольких переменных.

Вычисление экстремума функции многих переменных z=f(x₁,x₂,…,x_n) осуществляет команда:

[x, z] = fminsearch(name, x0 [, options]

где:

• name - имя М-функции, вычисляющей значение z=f(x₁,x₂,…,x_n), зависящей от n переменных;
• x0 – вектор из n элементов, содержащий координаты точки начального приближения;
• options – параметры, управляющие ходом решения;
• x - из n элементов, содержащий координаты точки, в которой достигается минимум функции;
• z – значение функции в точке с координатами x.

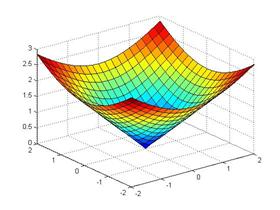
Пример:

Найти минимум функции

[z,f] = fminsearch(@(x) sqrt(x(1)^2+x(2)^2), [2,2])

%Построение графика

[x y]=meshgrid(-2:0.2:2, -2:0.2:2);

z=sqrt(x.^2+y.^2);

surf(x,y,z);

Результат:

z =

1.0e-004 *

-0.4133 -0.1015

f =

4.2559e-005

Примеры:

mf.m

min.m