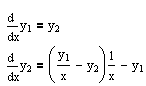Дифференциальные уравнения и системы уравнений Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]). Входными параметрами этих функций являются:
Все функции возвращают:
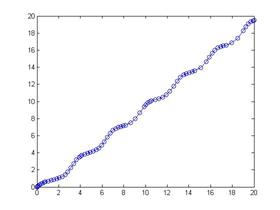
В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса. Пример: В М-файле с именем pr7.m пишем: function f=pr7(x,y) f=cos(x+y)+(3/2)*(x-y); end Потом в командном окне вызываем функцию ode113: ode113(@pr7,[0 20],0) %Метод Адамса: @pr7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 - условие: y(0)=0 Результатом будет график:
Пример: Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:
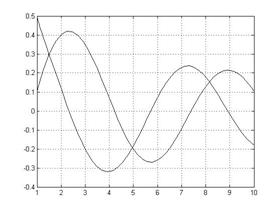
y1(0) = 0.1; y2(0) = 0.5 В М-файле с именем pr8.m пишем: function dy=pr8(x,y) dy=zeros(2,1); dy(1)=y(2); dy(2)=((y(1)/x)-y(2))*(1/x)-y(1); end Потом в командном окне вызываем функцию ode45: [x,y]=ode45(@pr8,[1 10], [0.1 0.5]); plot(x,y,'-k') grid; Результатом будет график:
Примеры: |