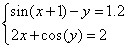Нелинейные уравнения и системы

В общем случае аналитическое решение уравнения f(х) = 0 можно найти только для узкого класса функций. Чаще всего приходится решать его численными методами. Численное решение уравнения проводят в два этапа:

  • отделяют корни уравнения, то есть находят достаточно тесные промежутки, в которых содержится только один корень, их называют интервалами изоляции корня, и определить их можно, изобразив график функции или любым другим методом, основанным на том, что непрерывная функция f(x) имеет на интервале [а; b] хотя бы один корень; если она поменяла знак f(a).f(b) < 0, а и b называют пределами интервала изоляции;
  • на втором этапе проводят уточнение отделенных корней, то есть находят корни с заданной точностью.

Любое уравнение P( х) = 0, где Р(х) - это многочлен, отличный от нулевого, называется алгебраическим уравнением (полиномом) относительно переменных x. Всякое алгебраическое уравнение относительно х можно записать в виде:

а0хn+ a1xn-1 + … + аn-1х+аn=0,

где а0 ≠ 0, n ≥ 1 и аi. - коэффициенты алгебраического уравнения n-й степени.

В MATLAB полином задается и хранится в виде вектора, элементами которого являются коэффициенты полинома от аn до a0.

Рассмотрим функции, предназначенные для действий над полиномами:

  • conv(p1, р2) - формирует вектор, соответствующий коэффициентам полинома степени n+m, полученного в результате умножения вектора p1 степени n на вектор р2 степени m, то есть вычисляет произведение двух полиномов;
  • deconv(pl, р2) -осуществляет деление полинома p1 на полином р2, то есть формирует вектор коэффициентов полинома, который является частным от деления p1 на р2; вызов функции в общем виде [q, r]=deconv(pl, р2) приводит к получению двух полиномов: q - частного от деления и r -остатка от деления;
  • polyval(p1, х) - вычисляет значение полинома с коэффициентами p1 в точке х;
  • polyder (p1 [, р2]) - формирует вектор коэффициентов полинома, являющегося производной от полинома с коэффициентами p1, то есть вычисляет производную от полинома; если в качестве аргументов указаны два вектора polyder(p1, р2), то производная вычисляется от произведения этих векторов, вызов функции в общем виде [q, r]= polyder (p1, p2) приведет к вычислению производной от частного pl/p2 и выдаст результат в виде отношения полиномов q и r.

Решить алгебраическое уравнение в MATLAB можно при помощи встроенной функции roots(p). Она формирует вектор, элементы которого являются корнями полинома с коэффициентами р. Наоборот, построить вектор р по заданному вектору его корней можно с помощью функции poly(х).

Для решения уравнений вида f(x)=0 в MATLAB применяют функцию fzero(name, x0), где:

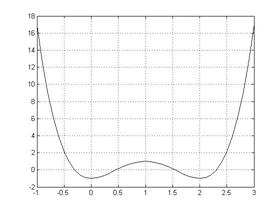
  • name – имя М-функции, вычисляющей левую часть уравнения;
  • x0 – начальное приближение к корню или интервал его изоляции [a, b];

Формат вызова функции может выглядеть так: [x, y]=fzero(name, x0), где x – корень уравнения, y – значение функции в точке x.

Пример(использование conv и deconv):

pl=[2 0 1];

p2=[1 0 0 -1];

%Умножение полиномов: (2х^2+1) (х^3-1) = 2х^5+х^3-2х^2-1

p=conv(p2,pl)

Результат:

p =

2 0 1 -2 0 -1

%Деление полиномов: (2х^5+х^3-2х^2-1) / (х^3-1) = (2х^2+1)

deconv(p,p2)

Результат:

ans =

2 0 1

Пример(использование polival):

p1=[2 1 0 -1 0 -3];

%3начение полинома (2х^5+х^4-х^2-3) в точке х=0

polyval(p1,0)

Результат:

ans =

-3

Пример(использование polider):

p1=[2 1 0 -1 0 -3];

polyder(p1); %Производная от p1

p2=[1 0 0 -1];

polyder(p1,p2); %Производная от (p1*p2)

[q, r]=polyder(p1,p2) %Производная от частного и остатка (p1/p2)

Результат:

q =

4 1 0 -9 -4 9 2 0

r =

1 0 0 -2 0 0 1

Пример(использование roots):

Найти корни полинома 2х4 - 8х3 + 8х2 - 1 = 0.

p=[2 -8 8 0 -1];

roots(p)

%Найдем графическое решение

x=-1:0.1:3;

y=polyval(p,x);

plot(x,y,'-k'),grid

Результат:

ans =

2.3066

1.5412

0.4588

-0.3066

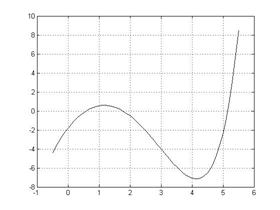
Пример:

Найти корни уравнения (ex/5)-2(x-1)2=0

В М-файле с именем ff.m пишем:

function y=f(x)

y=exp(x)/5-2*(x-1).^2;

end

Потом в командном окне пишем:

%Построение графика

x=-0.5:0.1:5.5;

y=exp(x)/5-2*(x-1).^2;

plot(x,y,'-k'), grid

[x(1),y(1)]=fzero('ff',[0 1]);

[x(2),y(2)]=fzero('ff',[1 2]);

[x(3),y(3)]=fzero('ff',[5 6]);

x

y

Результат:

x=

0.5778 1.7639 5.1477

y=

-0.0000 0.0000 0

Пример:

Решить систему уравнений:

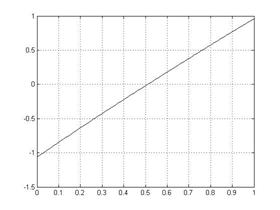
В М-файле с именем f25.m пишем:

function y=f25(x)

z=sin(x+1)-1.2;

y=2*x+cos(z)-2;

end

Потом в командном окне пишем:

x=0:0.01:1;

y=f25(x);

plot(x,y,'-k'), grid

Результатом будет график:

Потом находим решение системы(пишем в командном окне):

x=fzero('f25',0)

y=sin(x+1)-1.2

Результат:

x =

0.5102

y =

-0.2018

Примеры:

alg_ur1.m

alg_ur2.m

alg_ur3.m

alg_ur4.m

ff.m

f25.m

<<Назад

Далее >>