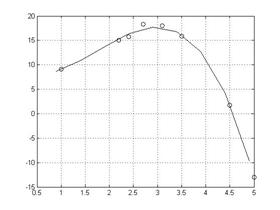
Обработка результатов методом наименьших квадратов

Метод наименьших квадратов позволяет по экспериментальным данным подобрать такую аналитическую функцию, которая проходит настолько близко к экспериментальным точкам, насколько это возможно.

Идея метода наименьших квадратов заключается в том, что функцию:

Y=f(x, a0, a1 ..., ak)

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений у_i. от расчетных Y. была наименьшей.

Пример:

x=[1 2.2 2.4 2.7 3.1 3.5 4.5 5];

y=[9.054 15.077 15.754 18.3 17.984 15.852 1.772 -13.042];

%Вычисление вектора коэффициентов полинома y=a1*x^3+a2*x^2+a3*x+a4

a=polyfit(x,y,3)

%Вычисление значений полиномов на интервале от 10 до 20

x1=0.9:0.5:5.1;

y1=polyval(a,x1);

%Построение графика полинома и экспериментальных точек в одной

%графической области

plot(x1,y1,'-k',x,y,'ok')

grid %Сетка

Результат:

a =

-1.3534 7.2257 -6.9270 10.0393

Пример:

mnk.m