9.6.1. Водородоподобная модель мелких уровней доноров и акцепторов
Будем рассматривать атом
донорной примеси как точечный положительный заряд Zq,
находящийся в диэлектрической среде со значением диэлектрической проницаемости ![]() . Потенциальная энергия взаимодействия избыточного электрона
с атомом примеси может быть записана в виде
. Потенциальная энергия взаимодействия избыточного электрона
с атомом примеси может быть записана в виде
|
|
(9.39) |
Проводя расчет энергетических уровней по Бору, получаем, что возможные энергетические состояния донорной примеси будут иметь водородоподобный вид [60]
|
|
(9.40) |
Для радиуса орбиты, по которой вращается электрон вокруг примесного атома, получаем
|
|
(9.41) |
Энергия основного состояния (n=1) получила
название энергии ионизации ![]() . Величина ее будет
. Величина ее будет
|
|
(9.42) |
В формуле (9.42) энергия ионизации выражена в электронвольтах, а численное значение энергии ионизации для атома водорода также рассчитано в электронвольтах.
Оценка энергии ионизации
донорного состояния показывает, что для кремния (![]() =12) она будет составлять чуть меньше 0,1 эВ, а для германия
(
=12) она будет составлять чуть меньше 0,1 эВ, а для германия
(![]() =16) она будет менее 0,05 эВ. Радиус боровской орбиты для
водородоподобного атома будет в
=16) она будет менее 0,05 эВ. Радиус боровской орбиты для
водородоподобного атома будет в ![]() раз больше, чем для
атома водорода. Для n-GaAs эта величина будет
составлять 85 Å. Для акцепторных состояний формализм расчета сохраняется.
раз больше, чем для
атома водорода. Для n-GaAs эта величина будет
составлять 85 Å. Для акцепторных состояний формализм расчета сохраняется.
Приведенные оценки
показывают, что водородоподобная модель описывает мелкие энергетические
состояния доноров и акцепторов, глубина локализации которых сравнима с тепловой
энергией ![]() . Следовательно, мелкие энергетические состояния при комнатной температуре будут полностью
находиться в ионизованном состоянии.
. Следовательно, мелкие энергетические состояния при комнатной температуре будут полностью
находиться в ионизованном состоянии.
Кроме мелких энергетических состояний, в полупроводниках ряд примесей формирует глубокие энергетические уровни. Для их описания используются представления о потенциале взаимодействия в виде кулоновского потенциала с экранировкой. Ниже, на рис. 9.16, приведены измеренные значения энергии ионизации примесных состояний в монокристаллах кремния, германия и арсенида галлия.
|
|
Рис. 9.16. Экспериментальные значения энергии ионизации примесных
состояний в чистых монокристаллах кремния, германия и арсенида галлия [13,
42] |
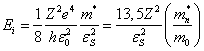 .
.