9.5. Движение электрона в периодическом поле кристалла под действием внешнего поля. Эффективная масса электрона
Вследствие того что в кристалле на электрон действует периодическое поле решетки, он приобретает некоторые свойства, в корне отличающие его от классической частицы [60, 82].
Пусть на вещество наложено
внешнее электрическое поле E, тогда
сила, действующая на электрон, ![]() . Скорость движения электрона равна групповой скорости
распространения волн
. Скорость движения электрона равна групповой скорости
распространения волн
|
|
(9.33) |
т. к. ![]() .
.
За время dt внешняя сила F совершает работу по перемещению электрона
|
|
(9.34) |
Отсюда
|
|
(9.35) |
Продифференцируем выражение
(9.33) для групповой скорости ![]() по времени и определим
ускорение электрона:
по времени и определим
ускорение электрона:
|
|
(9.36) |
Подставим сюда из формулы
(9.35) ![]() , тогда
, тогда
|
|
(9.37) |
Эта формула выражает второй
закон Ньютона. Под действием внешней силы F,
возникающей при наложении поля, электрон движется в среднем так, как двигался
бы под действием этой силы свободный электрон некоторой массы ![]() , определяемой соотношением
, определяемой соотношением
|
|
(9.38) |
Значение массы ![]() носит название эффективной массы электрона в решетке.
носит название эффективной массы электрона в решетке.
Для свободного электрона,
энергия которого определяется как![]() , эффективная масса
, эффективная масса ![]() принимает значение
массы покоя электрона m.
принимает значение
массы покоя электрона m.
Эффективная масса не является массой в ее обычном понимании. Она не определяет ни гравитационных, ни инерционных свойств электрона. По величине она может быть как больше, так и меньше массы свободного электрона, а по знаку – как положительной, так и отрицательной.
Рассмотрим следующий пример.
Пусть в первой зоне Бриллюэна находится один свободный электрон, который в
отсутствие внешнего поля располагается на дне зоны. Приложим к кристаллу
внешнее поле ![]() , под действием которого электрон будет ускоряться,
его кинетическая энергия будет расти, что приведет к его переходу на более
высокие энергетические уровни зоны.
, под действием которого электрон будет ускоряться,
его кинетическая энергия будет расти, что приведет к его переходу на более
высокие энергетические уровни зоны.
При небольших значениях
волнового числа k, пока кривая ![]() остается параболой
(рис.9.14),
остается параболой
(рис.9.14), ![]() и скорость движения
электрона
и скорость движения
электрона ![]() линейно растет с
ростом k, а эффективная масса
линейно растет с
ростом k, а эффективная масса ![]() остается практически
постоянной и равной массе покоя электрона. По мере удаления от нуля кривая
остается практически
постоянной и равной массе покоя электрона. По мере удаления от нуля кривая ![]() отходит от параболы,
нарастание скорости с увеличением k
замедляется, а следовательно, увеличивается эффективная масса
отходит от параболы,
нарастание скорости с увеличением k
замедляется, а следовательно, увеличивается эффективная масса ![]() . В точке А (точка
перегиба) первая производная энергии по волновому числу
. В точке А (точка
перегиба) первая производная энергии по волновому числу ![]() максимальна, а вторая
производная
максимальна, а вторая
производная ![]() обращается в нуль.
обращается в нуль.
Поэтому при значении
волнового числа ![]() , соответствующего точке перегиба зависимости
, соответствующего точке перегиба зависимости ![]() , скорость движения электрона максимальна, а эффективная
масса
, скорость движения электрона максимальна, а эффективная
масса ![]() обращается в
бесконечность. При значениях
обращается в
бесконечность. При значениях ![]() эффективная масса
электрона
эффективная масса
электрона ![]() меняет знак и
становится отрицательной. Скорость движения электрона при
меняет знак и
становится отрицательной. Скорость движения электрона при ![]() уменьшается, хотя
направление внешней силы сохраняется. В точке В (
уменьшается, хотя
направление внешней силы сохраняется. В точке В (![]() − граница зоны Бриллюэна) электрон испытывает
брэгговское отражение и появляется в точке
− граница зоны Бриллюэна) электрон испытывает
брэгговское отражение и появляется в точке ![]() . В интервале
. В интервале ![]() он ускоряется в
направлении, противоположном действию внешней силы, и его скорость меняется от
нуля до максимального значения, а эффективная масса – от массы покоя до
он ускоряется в
направлении, противоположном действию внешней силы, и его скорость меняется от
нуля до максимального значения, а эффективная масса – от массы покоя до ![]() . В точке
. В точке ![]() знак эффективной массы
меняется на положительный, и в интервале
знак эффективной массы
меняется на положительный, и в интервале ![]() электрон ускоряется в
направлении действия внешней силы.
электрон ускоряется в
направлении действия внешней силы.
|
|
|
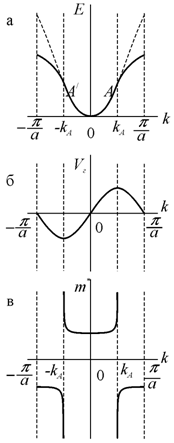
Рис. 9.14. Зависимость от волнового числа: а –
энергии, б – скорости, |
Наличие анизотропии
кристаллов обуславливает анизотропию динамических свойств электронов при их
движении. Вследствие этого эффективная масса является величиной тензорной. Чаще
всего анизотропия проявляется в двух направлениях, и поверхности постоянной
энергии имеют вид эллипсоидов вращения. В этом случае эффективная масса
подразделяется на эффективную массу в продольном направлении ![]() и эффективную массу в
поперечном направлении
и эффективную массу в
поперечном направлении ![]() . При отсутствии анизотропии
поверхность постоянной энергии имеет вид сферы и эффективная масса
является величиной скалярной. В табл. 9.3 [89] приведены экспериментальные
значения эффективной массы электронов вблизи дна зоны проводимости для ряда
полупроводников.
. При отсутствии анизотропии
поверхность постоянной энергии имеет вид сферы и эффективная масса
является величиной скалярной. В табл. 9.3 [89] приведены экспериментальные
значения эффективной массы электронов вблизи дна зоны проводимости для ряда
полупроводников.
Таблица 9.3
Эффективная масса электронов
вблизи дна зоны
проводимости для ряда полупроводников
|
Вещество |
|
|
|
Т (К) |
|
Si |
|
0,1905 |
0,9163 |
1,26 |
|
Ge |
|
0,08152 |
1,588 |
1,4 |
|
AlAs |
|
0,19 |
1,56 |
|
|
AlSb |
|
0,23 |
1,64 |
300 |
|
GaN |
0,28 |
|
|
300 |
|
GaP |
|
0,21 |
7,25 |
|
|
GaAs |
0,067 |
|
|
296 |
|
GaSb |
0,04 |
|
|
|
|
InP |
0,077 |
|
|
300 |
|
InAs |
0,027 |
|
|
300 |
|
InSb |
0,013 |
|
|
300 |
|
Cu2O |
0,99 |
|
|
|
Для дырок валентной зоны
анизотропия кристалла в меньшей мере влияет на динамические характеристики,
поскольку дырки являются способом описания коллективного движения электронов в
неполностью заполненной валентной зоне. Для дырок характерно влияние
спин-орбитального расщепления, которое обуславливает появление зоны тяжелых ![]() и легких
и легких ![]() дырок. В табл. 9.4
[89] приведены характеристические параметры для изоэнергетической поверхности
вблизи вершины валентной зоны, описывающие спин-орбитальное взаимодействие, и
эффективная масса легких и тяжелых дырок, а также эффективная масса,
описывающая динамические свойства с участием обоих типов дырок
дырок. В табл. 9.4
[89] приведены характеристические параметры для изоэнергетической поверхности
вблизи вершины валентной зоны, описывающие спин-орбитальное взаимодействие, и
эффективная масса легких и тяжелых дырок, а также эффективная масса,
описывающая динамические свойства с участием обоих типов дырок ![]() для ряда
полупроводников.
для ряда
полупроводников.
Таблица 9.4
Характеристические параметры
для изоэнергетической поверхности
вблизи вершины валентной зоны и эффективная масса дырок
для ряда полупроводников при 300 К
|
Вещество |
A |
B |
ïCï |
|
|
|
|
Алмаз |
|
|
|
0,7 |
2,18 |
1,06 |
|
Si |
-4,29 |
-0,68 |
4,87 |
0,153 |
0,52 |
0,234 |
|
Ge |
-13,38 |
-8,48 |
13,15 |
0,043 |
0,34 |
0,084 |
|
AlP |
-3,47 |
-0,130 |
3,96 |
0,20 |
0,63 |
0,29 |
|
AlAs |
-4,03 |
-2,09 |
4,63 |
0,15 |
0,76 |
0,24 |
|
AlSb |
-4,12 |
-2,09 |
4,71 |
0,14 |
0,94 |
0,29 |
|
GaAs |
-6,98 |
-4,5 |
6,2 |
0,068 |
0,5 |
0,133 |
|
GaP |
-4,20 |
-1,97 |
4,60 |
0,16 |
0,54 |
0,24 |
|
GaSb |
-11,7 |
-8,19 |
11,07 |
0,047 |
0,3 |
0,12 |
|
InAs |
-19,7 |
-16,8 |
13,66 |
0,025 |
0,41 |
0,089 |
|
InP |
-6,28 |
-4,17 |
6,24 |
0,089 |
0,85 |
0,17 |
|
InSb |
-35 |
-31,4 |
20,92 |
0,016 |
0,39 |
0,47 |
|
Cu2O |
|
|
|
0,58 |
|
0,69 |