9.4. Структура энергетических зон

Как уже было сказано выше, зоны разрешенных энергий имеют не сплошную структуру. Каждая из них состоит из дискретного набора очень близко расположенных уровней, представляющих собой энергетический спектр электрона, движущегося в периодическом поле кристаллической решетки. Стационарные состояния такого электрона описываются функцией Блоха (9.3) и энергетическим спектром (или законом дисперсии) , где  - волновой вектор, а n - номер энергетической зоны. Периодичность потенциала в кристалле обуславливает периодичность энергии  в -пространстве (, где - вектор обратной решетки.

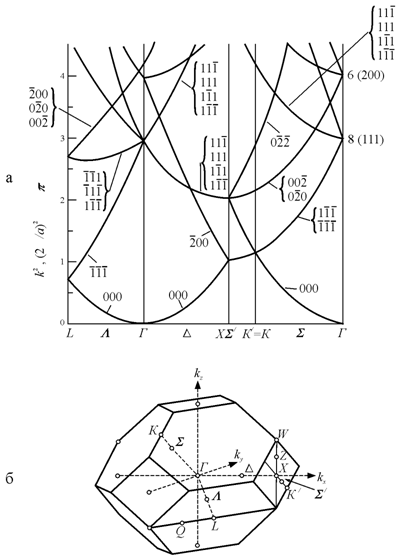
На рис. 9.11 показан вид зоны Бриллюэна для гранецентрированного кубического кристалла (рис. 9.11, б), а рис. 9.11, а иллюстрирует положение границ энергетических зон для такого кристалла с указанием направлений и характерных точек внутри зоны Бриллюэна.

 

Здесь символом Г обозначен центр зоны Бриллюэна, а символами D, L, L, S, K, W – симметричные точки в зоне Бриллюэна для гранецентрированного кубического кристалла. Положение этих точек определяется с использованием методов теории групп [5]. Направления D, L,S для ГЦК ячейки будут соответственно [100], [111], [110] .

 

Методы расчета зонной структуры

Расчет зонной структуры для реальных твердых тел проводится с использованием аппарата квантовой механики и теории групп. Наибольшее распространение получили методы с использованием приближения слабой связи. В этом методе в качестве нулевого приближения используются волновые функции свободного электрона, а потенциал взаимодействия атомных остовов рассматривается как возмущение. Поскольку точное значение потенциала определить трудно, используют модельные значения псевдопотенциала с учетом экранировок. В других методах, получивших название «приближение сильной связи», в качестве нулевого приближения используют волновые функции изолированных атомов. При этом интегралы перекрытий волновых функций не рассчитываются, а подбираются так, чтобы расчетный энергетический спектр совпадал с экспериментальным в выделенных точках зоны Бриллюэна.

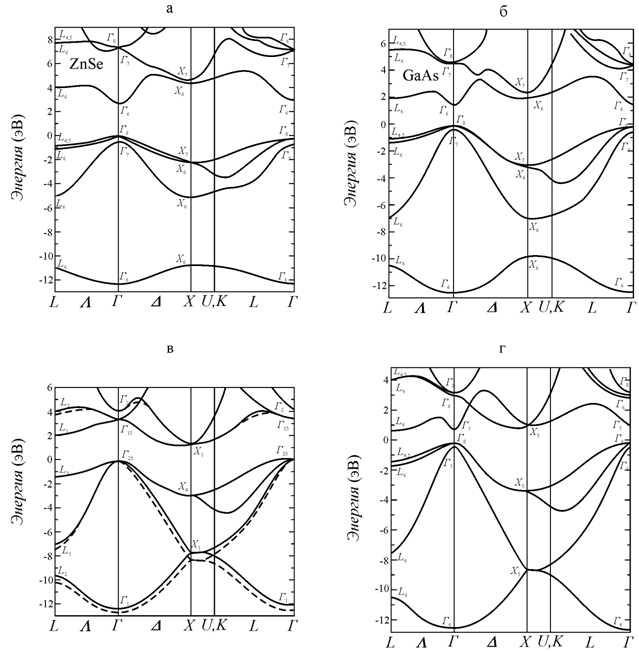
Зависимость энергии от волнового вектора в реальных материалах определяется как типом кристаллической структуры, так и сортом атомов, образующих то или иное соединение. На рис. 9.12 в качестве примера приведена рассчитанная зонная структура полупроводниковых соединений группы А₂В₆ (селенида цинка ZnSe), группы А₃В₅ (арсенида галлия GaAs) и элементов четвертой группы - кремния Si и германия Ge.

 

 

Рис. 9.12. Зонная структура  полупроводников: а - селенида цинка ZnSe; б - арсенида галлия GaAs; в - кремния Si; г - германия Ge [89, 93, 103]

 

Для германия и кремния элементарная ячейка является ГЦК и описывается структурным типом алмаза. Как следует из рис. 9.12 в, г, в этом случае вершина валентной зоны находится в центре зоны Бриллюэна, а дно зоны проводимости находится в других областях зоны Бриллюэна. Для такого типа кристаллических структур в генерационно-рекомбинационных процессах будут превалировать непрямые переходы и указанные полупроводники будут оптически не активны.

В арсениде галлия элементарная ячейка описывается структурным типом цинковой обманки. Как следует из рис. 9.12 а, в этом случае вершина валентной зоны и дно зоны проводимости находится в центре зоны Бриллюэна. Для такого типа кристаллических структур в генерационно-рекомбинационных процессах будут превалировать

прямые переходы и арсенид галлия будет оптически активным материалом.

В параграфе 9.2.1 обсуждалось возникновение энергетических зон в твердых телах при сближении атомов, их образующих. Внешние возмущения за счет силового поля взаимодействующих атомов снимает вырождение, и n-кратно вырожденные уровни расщепляются в зоны разрешенных энергий. Энергетические параметры зон определяются характеристиками потенциала взаимодействия атомов.

В реальных твердых телах межатомные расстояния зависят от температуры и давления. Изменение этих параметров меняет перекрытие волновых функций и потенциалы взаимодействия, а, следовательно, и энергетические параметры зонной структуры. Наиболее простым и доступным для наблюдения параметром зонной структуры является ширина запрещенной зоны E_g. Этому значению соответствует энергетический зазор между минимумом в зависимости E(k) для зоны проводимости и максимумом в зависимости E(k) для валентной зоны. Валентной зоной в полупроводниках называют последнюю полностью заполненную электронами зону разрешенных энергий, а зоной проводимости – следующую за ней полностью пустую зону разрешенных энергий. Отметим, что минимумы и максимумы  зависимости E(k) для различных полупроводников могут находиться как при k = 0, так и при  k ≠ 0. В табл. 9.2 символами  d и i отмечены полупроводники соответственно с прямыми и непрямыми переходами.

 Зависимость ширины запрещенной зоны E_g от температуры Т и давления р описывается эмпирическим соотношением

.

(9.32)

Параметры a и b в уравнении (9.32) являются характерными для каждого полупроводника и определяют изменение ширины запрещенной зоны от температуры и давления. В таблице 9.1 [89] приведены значения параметров a и b, определяющих изменение ширины запрещенной зоны E_g от температуры T и давления p.

 

Таблица 9.1

Значения параметров a и b,
определяющих ширину запрещенной зоны E_g
некоторых чистых полупроводников и полупроводниковых
соединений при различных температурах T

 

Характерные значения ширины запрещенной зоны E_g при абсолютном нуле и комнатной температуре для различных полупроводников приведены в табл. 9.2 [89, 103]. Как видно из данных этой таблицы, с ростом температуры от T=0К до комнатной T=300К для большинства полупроводников происходит уменьшение ширины запрещенной зоны. Для отдельных узкозонных полупроводников (например, селенида свинца PbSe) ширина запрещенной зоны с ростом температуры возрастает.

 

Таблица 9.2

Ширина запрещенной зоны при абсолютном нуле и комнатной температуре
для различных полупроводников: i − в полупроводниках с непрямыми переходами,
d − в полупроводниках с прямыми переходами

 

На основе зонной теории легко классифицировать вещества на металлы, полупроводники и диэлектрики:

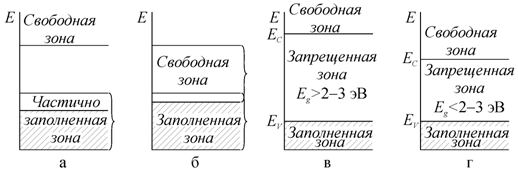
1.      К группе металлов относятся тела, у которых над целиком заполненными зонами располагается зона лишь частично заполненная (рис. 9.13, а). Частично заполненная зона возникает, когда атомный уровень, из которого она образуется, заполнен не полностью (например, у щелочных металлов).

 

Рис. 9.13. Заполнение зон электронами: а, б - в металлах; в - в диэлектриках; г - в полупроводниках (- вершина валентной зоны,  – дно зоны проводимости, Eg – ширина запрещенной зоны) [74]

 

Такая ситуация наблюдается и тогда, когда происходит наложение зон на пустые или частично заполненные зоны (бериллий, щелочно-земельные металлы) (рис. 9.13, б).

В твердых телах с такой структурой энергетических зон, при приложении внешнего электрического поля, повышающего энергию электронов, возможен их переход на более высокие энергетические уровни. Поскольку эти энергетические уровни находятся в той же зоне, образуют квазинепрерывный спектр, то переходы между ними возможны. Как макроскопический эффект эти переходы проявляются в протекания электрического тока через металлы при приложении электрического поля.

2.      К диэлектрикам относятся тела, у которых над целиком заполненными зонами располагаются полностью пустые, отделенные широким запрещенным интервалом (алмаз и со структурой алмаза) (рис. 9.13, в). Если валентная зона заполнена полностью и отделена от близлежащей широкой энергетической щелью, то внешнее поле не в состоянии изменить энергию электронов. Следовательно, в диэлектриках электрический ток не протекает.

3.      К группе полупроводников относятся вещества, имеющие сравнительно узкую запрещенную зону. К ним относятся германий, селен и другие (рис. 9.13, г). В таких твердых телах за счет флуктуаций тепловой энергии возможен переход электронов из полностью заполненной зоны в лежащую над ней зону разрешенных энергий. Полупроводники имеют промежуточное значение проводимости между металлами и диэлектриками.