9.3. Приближение почти свободных электронов. Модель Кронига–Пенни

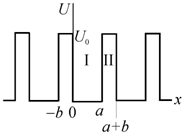
В модели почти свободных электронов, которую предложили Крониг и Пенни, рассматривается движение электрона в линейной цепочке прямоугольных потенциальных ям. Ширина ям равна a, и они отдельны друг от друга потенциальными барьерами толщиной b и высотой . Длина цепочки равна L, а период цепочки равен .

 

Рис. 9.7. Зависимость потенциальной энергии электрона от межатомного расстояния в модели Кронига–Пенни

 

Пусть E – энергия электрона. Состояние электрона описывается уравнением Шредингера:

.

(9.26)

Решение этого уравнение разбивается на две части:

1.      Для области I (рис. 9.7), где потенциальная энергия , волновая функция, являющаяся решением уравнения (9.26), может быть представлена в виде

.

(9.27)

Первое слагаемое в уравнении (9.27) соответствует прямой волне, а второе – волне, отраженной от потенциального барьера.

2.      Для области II (рис. 9.7), где , волновую функцию можно записать в виде

.

(9.28)

В уравнениях (9.27) и (9.28) коэффициенты , ; величины A, B, C, D - некоторые константы.

Подставим вместо  и  одномерную функцию Блоха  и найдем вид периодической функции  в областях I и II:

, .

(9.29)

Для того чтобы определить коэффициенты A, B, C, D, используем тот факт, что функция  и ее первая производная непрерывны в местах скачка потенциала. Например, в точке

, .

Кроме того, функции  обладают свойством периодичности с периодом

, .

Подставляя эти условия в систему уравнений (9.29) для потенциалов  и , получим четыре уравнения. Известно, что такая система уравнений будет иметь ненулевые решения при условии, что определитель, составленный из коэффициентов при A, B, C, D, будет равен нулю. Это требование приводит к уравнению:

.

(9.30)

Рассмотрим предельный случай, устремив ширину барьера b к нулю и увеличим высоту барьера, устремив ее к бесконечности (). При этом потребуем, чтобы произведение  оставалось постоянным. Обозначим , где P − величина, характеризующая прозрачность барьера. Для этого предельного случая уравнение (9.30) примет вид

.

(9.31)

Уравнение (9.31) выражает зависимость энергии электрона, которая входит в коэффициент α, от волнового числа k для барьеров различной прозрачности P. Поскольку  не может быть больше  (), то и левая часть уравнения (9.31) лежит в этих же пределах. Эти значения определяют области разрешенных энергий электрона – энергетические зоны (рис. 9.8). Они отделены друг от друга полосами запрещенных энергий – запрещенными зонами. С увеличением энергии электрона ширина разрешенных зон увеличивается, а запрещенных уменьшается. Ширина зон зависит также от параметра прозрачности барьера P. При  разрешенные зоны сужаются, превращаясь в дискретные уровни, соответствующие , где . Тем самым мы приходим к случаю электрона в изолированном атоме. При стремлении прозрачности барьера к нулю , наоборот, исчезают запрещенные зоны, и электрон становится свободным. Покажем зависимость энергии электрона E от модуля волнового вектора  (рис. 9.9).

 

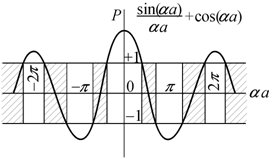
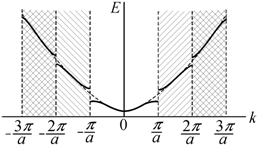
Рис. 9.8. Зависимость левой части уравнения (9.9) от aа. Интервалы допустимых значений заштрихованы [74]	Рис. 9.9. Энергетические зоны линейной цепочки атомов в расширенной зонной схеме [74]

 

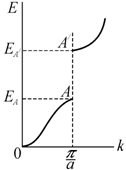
Внутри каждой зоны энергия электрона растет с ростом значения модуля волнового вектора. При значениях , где , энергия терпит разрыв (рис. 9.10), приводящий к образованию запрещенных зон.

 

Рис. 9.10. Разрыв энергии электрона при

 

Для случая трехмерной решетки, где , запрещенные зоны различных направлений в кристалле могут налагаться друг на друга, образуя абсолютно запрещенную зону для кристалла в целом. Возможен случай, когда разрешенные зоны одного направления накладываются на запрещенные зоны другого, тогда образуется разрешенная зона энергий без разрыва. Энергетический интервал между зонами разрешенных энергий в реальных твердых телах является важной физической характеристикой, определяющей целый ряд свойств материала. Этот интервал называется шириной запрещенной зоны, и его принято обозначать .