9.2.1. Энергетические зоны
Уменьшение высоты
потенциальных барьеров при сближении атомов (рис. 9.2) приводит к тому, что валентные
электроны в металле перестают быть локализованными в конкретном атоме, а
переходят от одного атома к другому. Может показаться, что такие переходы
приводят к нарушению принципа Паули и в любой момент в атоме может оказаться
несколько электронов с одинаковой энергией. Однако при образовании кристалла
происходит не только уменьшение высоты потенциального барьера, но и
качественное изменение энергетических уровней электронов в атомах.
Воспользуемся соотношением неопределенности энергии-времени ![]() , где
, где ![]() -
время нахождения электрона в энергетическом состоянии, характеризующемся
интервалом энергии от E до E+DE. Величина DE
определяет ширину энергетического уровня, если известно время пребывания на нем
электрона. В изолированном атоме время Dt сколь
угодно велико, поэтому DE исчезающе мало.
-
время нахождения электрона в энергетическом состоянии, характеризующемся
интервалом энергии от E до E+DE. Величина DE
определяет ширину энергетического уровня, если известно время пребывания на нем
электрона. В изолированном атоме время Dt сколь
угодно велико, поэтому DE исчезающе мало.
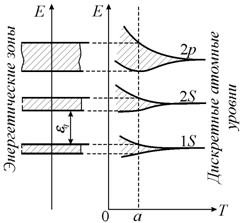
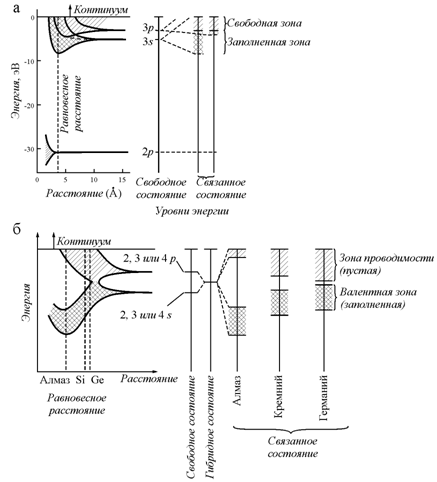
В кристалле скорость движения электронов V ~ 105 м/с, поэтому около данного узла решетки он находится в течение приблизительно 10-15 с. Приняв это значение времени за Dt, получим ширину энергетического уровня DE ~ 1 эВ. Такой результат свидетельствует о том, что при образовании кристалла энергетический уровень электрона расщепляется в энергетическую зону (рис. 9.3). Эффект расщепления энергетических уровней на зоны для металлического натрия и элементов IV группы таблицы Менделеева (алмаз, кремний и германий) показан на рис. 9.4.
|
|
|
Рис. 9.3 Расщепление энергетических уровней на зоны |
|
|
|
Рис. 9.4. Образование энергетических зон: а - в металлическом натрии; б - в элементах IV группы элементов: алмаз, кремний и германий [89] |
Следовательно, при образовании кристалла возникает система энергетических зон. Однако энергетическая зона – это не непрерывный ряд значений энергии электронов, а система близких друг к другу дискретных уровней энергии.
Если обобществленные
электроны достаточно сильно связаны с атомом, то их потенциальную энергию можно
представить как ![]() , где
, где ![]() − потенциальная
энергия электрона в изолированном атоме, а dU – поправочный член, учитывающий
влияние соседних атомов.
− потенциальная
энергия электрона в изолированном атоме, а dU – поправочный член, учитывающий
влияние соседних атомов.
По мере сближения изолированных атомов и образования из них решетки каждый атом попадает во все возрастающее поле своих соседей. Каждый из уровней атома расщепляется на N подуровней, где N – количество атомов в кристалле. При ширине уровня 1 эВ и количестве атомов в 1 см3, равном 1023 атомов/см3, расстояния между подуровнями чрезвычайно малы, и такую область можно рассматривать как энергетическую зону с квазинепрерывным спектром энергетических состояний. Следовательно, моноэнергетический уровень расщепляется в энергетическую зону, получившую название зоны разрешенных энергий. Зоны разрешенных энергий отделены друг от друга зонами запрещенных энергий.
Выясним физический смысл
существования запрещенных зон. Рассмотрим одномерную решетку (линейную цепочку
одинаковых атомов) с периодом а. В
этом случае распределение электронов по энергиям можно изобразить в виде
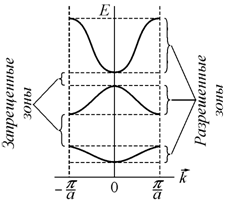
приведенной зонной диаграммы (рис. 9.5). Это распределение характеризуется
разрывом при значениях волнового числа ![]() , что и создает область запрещенных энергий. В одномерном
случае формула Вульфа-Брэггов
, что и создает область запрещенных энергий. В одномерном
случае формула Вульфа-Брэггов ![]() принимает вид
принимает вид
|
|
(9.25) |
Первые отражения возникают
при условии, что ![]() , и первая зона запрещенных энергий (энергетическая щель) оказывается
соответствующей именно этим значениям волнового числа. Последующие
энергетические щели возникают при следующих положительных и отрицательных
значениях k. Отражение при
, и первая зона запрещенных энергий (энергетическая щель) оказывается
соответствующей именно этим значениям волнового числа. Последующие
энергетические щели возникают при следующих положительных и отрицательных
значениях k. Отражение при ![]() возникает вследствие
того, что волны, отраженные от соседних атомов в цепочке, усиливаются в
результате интерференции, причем разность фаз при данном значении волнового
числа k будет составлять
возникает вследствие
того, что волны, отраженные от соседних атомов в цепочке, усиливаются в
результате интерференции, причем разность фаз при данном значении волнового
числа k будет составлять ![]() . Область пространства волновых векторов (k-пространство) между значениями
. Область пространства волновых векторов (k-пространство) между значениями ![]() и
и ![]() , в этом примере носит название первой зоны Бриллюэна. Внутри
зоны Бриллюэна энергия квазинепрерывна, а на границах она имеет разрыв.
, в этом примере носит название первой зоны Бриллюэна. Внутри
зоны Бриллюэна энергия квазинепрерывна, а на границах она имеет разрыв.
Как было показано в
параграфе, 9.1 на амплитуду волновой функции свободного электрона, в
периодическом поле ионных остовов кристаллической решетки накладывается
дополнительное условие: она не остается постоянной, а периодически изменяется
или, иначе говоря, модулирована с периодом решетки. Волновая функция электрона
в этом случае имеет вид блоховской функции (9.24). Исходя из зонного характера
энергии электрона, можно утверждать, что внутри каждой разрешенной
энергетической зоны энергия электрона E является периодической
функцией волнового вектора ![]() (рис. 9.5).
(рис. 9.5).
|
|
|
Рис. 9.5 Зависимость энергии электрона от волнового вектора для одномерной моноатомной цепочки |
Конкретный вид зависимости ![]() определяется как
симметрией кристалла, так и типом атомов, его образующих. Анизотропия кристалла
обуславливает зависимость
определяется как
симметрией кристалла, так и типом атомов, его образующих. Анизотропия кристалла
обуславливает зависимость ![]() от
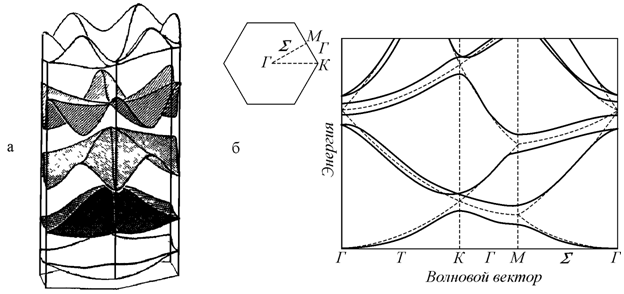
кристаллографического направления. На рис. 9.6 представлена трехмерная картина
изменения энергетических уровней в периодическом поле двумерной гексагональной
кристаллической решетки и дисперсия энергии электрона вдоль направления
наибольшей симметрии этой решетки. Из рис. 9.6, б видно, что энергетические
уровни свободного электрона претерпевают значительные изменения при наложении
периодического потенциала. Более подробно анализ этих зависимостей проведен в
разделе 9.4.
от
кристаллографического направления. На рис. 9.6 представлена трехмерная картина
изменения энергетических уровней в периодическом поле двумерной гексагональной
кристаллической решетки и дисперсия энергии электрона вдоль направления
наибольшей симметрии этой решетки. Из рис. 9.6, б видно, что энергетические
уровни свободного электрона претерпевают значительные изменения при наложении
периодического потенциала. Более подробно анализ этих зависимостей проведен в
разделе 9.4.
|
|
|
Рис. 9.6. Зависимости энергии электрона от волнового вектора: а − изменение энергетических уровней свободного электрона, находящегося в поле ненулевого периодического потенциала в случае двумерной гексагональной решетки; б − дисперсия энергии вдоль направлений наибольшей симметрии гексагональной решетки (пунктир показывает уровни свободного электрона) [89] |