9.1. Одноэлектронное приближение. Теорема Блоха

Решение задачи движения коллективизированных электронов в кристалле, вообще говоря, сложно, т. к. и количество электронов, и количество ионов очень велико. Приближенное решение может быть сведено к задаче движения одного (любого) электрона в поле периодически расположенных в кристалле ионов. Такой подход носит название одноэлектронного приближения. В этом приближении вводится ряд упрощающих условий:

1.      Большая разница масс атомных ядер и электронов приводит к очень большой разнице в скоростях движения. Поэтому при описании движения электрона можно не учитывать движение ядер, а рассматривать движение электрона в поле неподвижных ядер. Это условие получило название адиабатического приближения.

2.      Медленное движение ядер можно рассматривать не в поле, создаваемом мгновенным расположением электронов, а в поле, создаваемом средним пространственным распределением зарядов электронов.

3.      Взаимодействие каждого электрона с остальными, зависящее от мгновенного расположения всех электронов, рассматривается как взаимодействие электрона с самосогласованным полем, создаваемым средним пространственным распределением зарядов электронов.

В результате введения перечисленных упрощений уравнение Шредингера оказывается разрешимым и дает возможность определить значения энергии электрона в кристалле [54, 57, 67, 68]. Рассмотрим вопрос одноэлектронного приближения более подробно.

При обсуждении атомных орбиталей в гл. 2 было приведено уравнение Шредингера (2.30), описывающее стационарное (не зависящее от времени) состояние квантовых частиц. Оператор Гамильтона (гамильтониан), стоящий в левой части уравнения, можно представить в виде суммы , где  − оператор кинетической энергии частицы, имеющий вид  ( − оператор импульса, m − масса частицы), а  − ее потенциальная энергия. В общем случае потенциальная энергия частиц, составляющих твердое тело, складывается из энергий парного взаимодействия электронов с электронами, ядер с ядрами и электронов с ядрами. Такой подход делает задачу выяснения характера движения электронов в кристаллической решетке практически неразрешимой, поскольку уравнение Шредингера становится весьма сложным и решить его в аналитическом виде не удается. Однако, одноэлектронное приближение упрощает эту задачу.

Рассмотрим взаимодействие электрона с периодическим полем кристалла в одномерном случае [59]. Пусть  − потенциальная энергия электрона в одномерной периодически расположенной цепочке атомов, расстояние между которыми равно a. Трансляционная симметрия кристалла позволяет записать равенство

.

(9.1)

Поскольку электрон движется в поле с потенциалом , то гамильтониан в уравнении Шредингера, описывающий поведение электрона в кристалле, в одномерном виде можно записать как

,

(9.2)

а само уравнение Шредингера в виде

.

(9.3)

Так как  − периодическая функция, то она может быть разложена в ряд Фурье:

,

(9.4)

где , n − целые числа.

Вид функции   может быть достаточно сложен. Если внутри отрезка, равного периоду кристаллической решетки, находится лишь один ион, то функция потенциальной энергии имеет колоколообразный вид, если решетка более сложная − то  может представлять собой сумму функций такого типа.

Из свойств интегралов Фурье следует, что фурье-компоненты таких функций убывают с ростом параметра g. Кроме этого будем считать, что среднее значение потенциальной энергии по всей решетке  равно нулю. Подставляя уравнение (9.4) в (9.3), получим

.

(9.5)

Записывая оператор импульса в явном виде, уравнение (9.5) можно представить в виде

.

(9.6)

Определим вид волновой функции . Введем периодические граничные условия:

,

(9.7)

где L = Na − размер кристалла вдоль направления x, N − число атомов в решетке, расположенных вдоль направления x.  

Найдем решение уравнения (9.5) с учетом условия (9.7). Примем во внимание, что при  решение уравнения (9.6) должно представлять собой решение для свободных электронов. В этом случае удобно представить искомую волновую функцию  в виде суперпозиции плоских волн типа . Подстановкой такой функции в уравнение (9.7) можно убедиться в том, что для выполнения граничных условий необходимо, чтобы удовлетворялось равенство , откуда следует

,

(9.8)

где n − любое целое число.

Взаимодействие электрона с полем кристалла может привести к тому, что коэффициенты перед функциями  могут перестать быть постоянными. Конечно, они будут зависеть от волнового числа k, но по определению они не должны зависеть от координаты x. Это условие эквивалентно равенству

,

(9.9)

где  − коэффициенты, зависящие только от k.

Найдем теперь слагаемые в уравнении (9.6) после подстановки в них выражения (9.9).

,

(9.10)

 

.

(9.11)

Тогда с учетом соотношений (9.10) и (9.11) уравнение (9.6) можно представить в виде

(9.12)

Это уравнение можно упростить, используя свойство ортонормированности фурье-компонент с различными волновыми числами k и :

.

(9.13)

С учетом того, что  и , получим

(9.14)

Отсюда следует, что

(9.15)

Чтобы использовать указанное свойство для упрощения уравнения (9.12), умножим последнее на  и проинтегрируем по x от  до . Получим в зависимости от вида экспоненты с учетом , либо :

,

(9.16)

 

,

(9.17)

 

.

(9.18)

Суммируя, найдем

.

(9.19)

Все значения волновых чисел  и  равноправны, поэтому везде можно заменить  на . Кроме того, можно использовать замену . В результате получим систему уравнений относительно коэффициентов :

.

(9.20)

Система уравнений (9.20) является одной из форм уравнения Шредингера, однако, в отличие от исходного, она состоит не из дифференциальных, а из алгебраических уравнений, что значительно упрощает процедуру решения. Наиболее важной особенностью системы уравнений (9.20) является то, что она связывает коэффициенты . В силу этого соотношения коэффициенты  в волновой функции (9.9) не могут выступать самостоятельно, а входят вместе с совокупностью коэффициентов , аргументы которых различаются на . При этом коэффициенты  распадаются на группы коэффициентов , , , … с различными исходными значениями . Тогда волновая функция  будет состоять из совокупности волновых функций, в каждую из которых входят волновые функции вида . Очевидно, если выбрать исходные значения волнового вектора  так, чтобы они принимали все возможные значения между ближайшими значениями , то суммарный набор значений  будет включать все возможные значения.

Итак, мы получили, что волновая функция  будет состоять из волновых функций , имеющих вид

,

(9.21)

причем для определения всех волновых функций электронов требуется найти  со значениями волновых чисел, выбранных в интервале .

Проанализируем свойства волновой функции. Для этого преобразуем (9.21) к виду

.

(9.22)

Выражение в квадратных скобках (9.22) представляет собой ряд Фурье, следовательно оно описывает периодическую функцию

,

(9.23)

период которой равен a. Это означает, что волновая функция  равна произведению фазового множителя , который характеризует поведение свободных частиц на оси x, на периодическую функцию  с периодом, равным периодичности потенциала. Этот результат представляет знаменитую теорему Блоха, которая в трехмерном случае гласит: собственные функции волнового уравнения с периодическим потенциалом имеют вид произведения плоской волны  на функцию , периодическую в решетке кристалла:

.

(9.24)

Функцию (9.24) часто называют блоховской волновой функцией.

Таким образом, в периодическом поле кристалла на амплитуду волновой функции электрона накладывается дополнительное условие: она не остается постоянной, а периодически изменяется или, иначе говоря, модулирована с периодом, равным периоду решетки a.
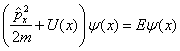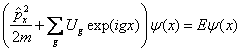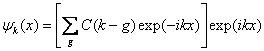