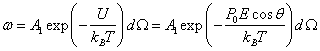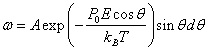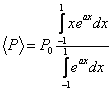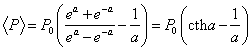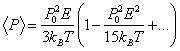8.3.3. Дипольная тепловая поляризация

Если в диэлектрике имеются слабо связанные друг с другом полярные молекулы, то под действием поля они могут более или менее легко разворачиваться. В результате возникает дипольная поляризация, зависящая от теплового движения. Расчет дипольной тепловой поляризации предложен Дебаем [25].

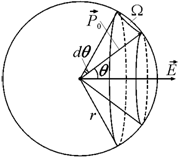
Пусть диэлектрик содержит N диполей, обладающих электрическим моментом . Рассмотрим ситуацию, когда какой-либо диполь ориентирован под углом  к направлению внешнего поля  (рис. 8.8).

 

Рис. 8.8. Ориентация диполя с дипольным моментом  во внешнем электрическом поле

 

Потенциальная энергия диполя в электрическом поле . Стремление системы к минимуму энергии означает стремление угла  к нулю, т. е. в этом случае все диполи стремятся ориентироваться в направлении поля. Тепловое же движение препятствует этому процессу. Следовательно, результирующий дипольный момент диэлектрика определяется статистическим равновесием между ориентирующим действием поля и разориентирующим действием теплового движения.

Индуцированный полем дипольный момент

,

(8.44)

где  – средний электрический момент молекулы в поле Е. Таким образом, задача сводится к нахождению среднего дипольного момента молекулы в направлении поля.

Вероятность того, что дипольный момент  направлен по отношению к полю под углом, лежащим в пределах от  до  и его вектор находится в пределах некоторого телесного угла dW (рис. 8.8), определяется распределением Больцмана:

,

(8.45)

где  – константа нормировки.

Телесный угол  опирается на шаровой пояс, вырезанный на сфере радиуса r двумя коническими поверхностями. Площадь этого пояса равна длине окружности , умноженной на ширину кольца , поэтому .

Если сфера имеет единичный радиус (r=1), то . Подставляя это выражение в формулу (8.45), получим

,

(8.46)

где новая постоянная величина .

Средний дипольный момент молекулы в электрическом поле .

Введем обозначения , , тогда среднее значение дипольного момента равно .

Постоянная А ищется из условия . Тогда

,

(8.47)

или

,

(8.48)

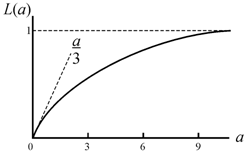
где  – функция Ланжевена. График функции L(a) приведен на рис. 8.9. Прокомментируем поведение кривой на представленном рисунке.

 

Рис. 8.9. Зависимость функции Ланжевена L(a) от величины a

 

При малых значениях а, т. е. в области низких температур и малых полей, функцию Ланжевена L(a) можно разложить в быстро сходящийся ряд: . Тогда среднее значение дипольного момента 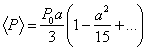, т. е.

.

(8.49)

При  второе и последующие слагаемые в (8.49) малы и их можно не учитывать. Тогда для N молекул суммарная поляризация будет

.

(8.50)

Физический смысл выражения (8.50) в том, что при малых полях средний дипольный момент в направлении поля пропорционален напряженности поля. Таким образом, тепловая поляризуемость, создаваемая в диэлектрике N молекулами , может быть выражена как

.

(8.51)

В сильных полях, когда потенциальная энергия диполя сравнима с тепловой энергией , пропорциональность нарушается и поляризация áPñ стремится к насыщению.

На практике условия, при которых a является очень большой величиной, никогда не достигаются. Например, для молекулы HCl в поле порядка  В/м величина , так что при комнатной температуре . Следовательно, с достаточно большой степенью точности величину L(a) в выражении (8.48) можно заменить на a/3. Тогда при низких температурах и в умеренных полях мы получим для тепловой (релаксационной) поляризации представленные выше выражения (8.50) и (8.51).