8.4. Связь между поляризуемостью и диэлектрической проницаемостью

Поляризация реальных диэлектриков имеет обычно сложный характер. Она является совокупностью отдельных простейших видов поляризации. Если n_m – концентрация частиц, участвующих в m-м виде поляризации, а a_m – поляризуемость этого вида, то результирующий дипольный момент единичного объема диэлектрика можно представить в виде

,

(8.52)

где m=1, 2, …, 6 (с учетом всех рассмотренных типов поляризации),  − макроскопическое поле в диэлектрике.

Однако при выводе этого выражения никак не учитывается то, что между атомами и молекулами реального тела, находящегося в конденсированном состоянии, всегда существуют силы взаимодействия. Все приведенные до сих пор рассуждения достаточно хорошо описывают поведение диэлектриков в газообразном состоянии, когда такие силы очень малы. Изучение же поляризации атомов и молекул в твердых телах или жидкостях становится значительно более сложной задачей, чем исследование этого явления в газах. Новое здесь заключается не в появлении дополнительных типов поляризации: атомы и молекулы, как в газах, так и в твердых и жидких телах, обладают электронной, ионной и дипольной поляризацией. Разница состоит в том, что локальное поле, действующее на атом в конденсированном состоянии вещества, не равно приложенному внешнему полю. В общем случае трудность составляет как раз вычисление локального поля.

Представим упрощенный вариант такого расчета в контексте связи между поляризуемостью диэлектриков и их диэлектрической проницаемостью [74].

Макроскопический параметр диэлектрика – его диэлектрическая проницаемость e. Она связана с дипольным моментом P и напряженностью поля E соотношением

 

.

(8.53)

Как уже было сказано выше, электрическое поле, действующее на атом или молекулу в диэлектрике Е_лок (локальное), не всегда совпадает со средним макроскопическим полем Е. Каждый атом или молекула находится в окружении себе подобных, и поля соседей действуют на него. Эти поля изменяются при наложении внешнего поля, т. к. молекулы (атомы) поляризуются. В результате численный расчет локального поля оказывается невероятно сложен. Лоренц предложил метод расчета локального поля, применимый для газов, неполярных жидкостей и кубических кристаллов.

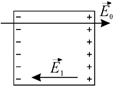
Действующее на какую-либо молекулу внутри кристалла поле Е_лок в методе Лоренца разбивается на векторную сумму полей

,

(8.54)

где  − это внешнее поле,  − поле, обусловленное зарядами на поверхности диэлектрика (деполяризующее поле) (рис. 8.10),  и  − поля, природа которых будет разъяснена несколько ниже.

 

Рис. 8.10. Внешнее поле  и поле , наведенное зарядами на поверхности диэлектрика

 

Сумма напряженностей внешнего  и деполяризующего  полей, присутствующая в уравнении (8.54), представляет собой макроскопическое поле в диэлектрике :

.

(8.55)

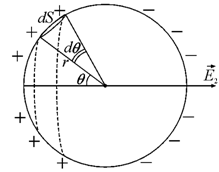
Для пояснения физического смысла полей  и  мысленно вырежем в диэлектрике сферу радиусом в несколько десятков межатомных расстояний (рис. 8.11).

 

Рис. 8.11. К пояснению физического смысла компонент  и  локального электрического поля

 

Действие молекул, находящихся вне сферы, на молекулу в центре ее опишем компонентой , а действие молекул, находящихся внутри сферы, на ту же молекулу – компонентой . Для вычисления поля  предположим, что все молекулы внутри сферы, кроме той, что находится в центре, изъяты. Поскольку диэлектрик поляризован, то на поверхности сферы возникает связанный заряд q.

Выделим на сфере элементарную поверхность dS, вырезанную телесным углом  и расположенную под углом  к направлению внешнего поля. Малый заряд, распределенный по этой поверхности, обозначим dq. Тогда напряженность поля, создаваемая зарядом  в центре сферы,

.

(8.56)

Выразим элементарный заряд dq через поверхностную плотность заряда  и площадь поверхности, на которой он локализован dS, как . Поверхностная плотность заряда связана с величиной поляризации и углом, под которым расположена площадка: , а величина . Тогда элементарный заряд

.

(8.57)

Подставим уравнение (8.57) в (8.56) и для нахождения полного поля  проинтегрируем полученное выражение по углу

.

(8.58)

Интеграл в уравнении (8.58) табличный и дает численное значение 2/3, поэтому окончательное выражение для искомой компоненты внутреннего поля будет иметь простой вид

.

(8.59)

Вычисление компоненты поля  для сложных структур весьма трудоемко. В случае кубической кристаллической решетки действия симметрично расположенных молекул относительно молекулы, находящейся в центре сферы, складываются, давая в сумме нуль. Поэтому для простейшего случая кубической структуры .

Учитывая вышесказанное, локальное поле можно теперь представить в виде

.

(8.60)

Подставляя это выражение в уравнение для результирующего дипольного момента (8.52), получим уравнение, известное как уравнение Клаузиуса-Мосотти:

,

(8.61)

позволяющее вычислять поляризуемость атомов (молекул) из измерения диэлектрических постоянных. Принимая в расчет суммарную поляризуемость тела a, состоящего из N частиц, уравнение (8.61) можно переписать в виде, более часто встречающемся в специальной литературе:

.

(8.62)

Величину  называют удельной поляризацией диэлектрика.