8.3.2. Ионная тепловая поляризация

Некоторые диэлектрики характеризуются тем, что в их структуре имеются слабо связанные ионы, которые обычно размещаются в междоузлиях или локализованы вблизи дефектов структуры. Тепловое движение может приводить к перемещению таких ионов из одних положений равновесия в другие путем преодоления некоторых потенциальных барьеров. Если внешнее поле отсутствует, то такие перемещения совершаются случайно и диэлектрик не поляризуется. Под действием электрического поля высота и форма потенциальных барьеров меняются, и характер перемещения становится упорядоченным. Такое упорядоченное перемещение ионов вызывает поляризацию, время релаксации которой составляет с в зависимости от типа диэлектрика и вида дефектов в нем.

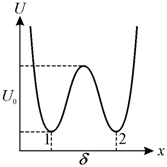
Рассмотрим ионную тепловую поляризацию более подробно (рис. 8.6).

Пусть ион находится в равновесии на дне потенциальной ямы (положение 1), отделенной от другой потенциальной ямы 2 энергетическим барьером .

 

Рис. 8.6. Потенциальный рельеф энергии иона в отсутствие внешнего электрического поля

 

Пространственно ямы разделены зазором d. Если энергия иона в какой-то момент превысит значение , то он может из потенциальной ямы 1 перейти в равновесное положение 2. Вероятность такого перехода равна .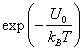

Пусть в единичном объеме диэлектрика содержится  слабосвязанных ионов, а n – частота их тепловых колебаний около положения равновесия. Тогда число частиц, преодолевших потенциальный барьер  в направлении оси x за 1 секунду, составит

.

(8.31)

Множитель  связан с тем, что по законам вероятности из всех  ионов только 1/6 будет перемещаться в положительном направлении x. Из всего остального числа ионов 1/6 будет перемещаться в отрицательном направлении оси x, а остальные 4/6 ионов будут соответственно перемещаться вдоль и против осей y и z. Поскольку каждый ион n раз в секунду движется в направлении x , то число «попыток» перескочить барьер в единицу времени составляет , но т. к. не все частицы смогут перейти этот барьер, то это число необходимо умножить на вероятность того, что у частицы имеется запас энергии  [56].

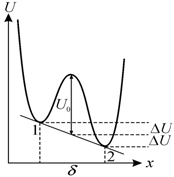
Если внешнего поля нет, то все перескоки ионов через потенциальный барьер равновероятны. Наложение внешнего поля вдоль оси x изменяет вид потенциального рельефа  (рис. 8.7).

Рис. 8.7. Зависимость потенциальной энергии иона от смещения x при наложении внешнего поля вдоль оси x

 

В результате для иона, находящегося в положении 1, высота потенциального барьера составит , а в положении 2 она будет . Соответственно вероятность перехода из 1 в 2 увеличивается, а из 2 в 1 будет уменьшаться. Если заряд иона равен e, то изменение высоты потенциального барьера под действием поля составит DU=eEd/2. Число перескоков в положительном направлении x доминирует над числом перескоков в обратном направлении, и в диэлектрике устанавливается асимметричное распределение зарядов, т. е. возникает некоторый дипольный момент.

Пусть Dn – уменьшение числа ионов в положении 1, равное увеличению их количества в положении 2. После включения поля и установления равновесия количества ионов в положениях 1 () и 2 () станут

.

(8.32)

Поскольку каждый избыточный ион создает дипольный момент dе, то в единице объема возникнет суммарный электрический дипольный момент

P=Dnde.

(8.33)

Тогда, по ранее найденным соотношениям, поляризуемость, приходящаяся на каждый переброшенный ион, составит

.

(8.34)

Найдем величину Dn, которая зависит от температуры диэлектрика T и напряженности внешнего электрического поля Е. Поскольку , то можно записать

.

(8.35)

Здесь первое слагаемое, обозначенное I, представляет собой число частиц, покинувших положение 1, а II – число частиц, перешедших в положение 2. Подставим в уравнение (8.35) значения  из уравнений (8.32). Тогда

.

(8.36)

Рассмотрим случай, когда внешнее поле слабое, т. е. . Тогда, используя разложение экспонент  в ряд и ограничиваясь двумя первыми слагаемыми, получим

.

(8.37)

Используя (8.37), приведем уравнение (8.35) к виду

.

(8.38)

Будем считать для упрощения, что среднее поле, действующее на каждый ион, одинаково во всем диэлектрике (Е=const), тогда вид потенциального рельефа в районе любого из слабосвязанных ионов тоже будет одинаков и DU=const. Введем обозначения

,

(8.39)

где t, как и ранее, является временем релаксации. Заменим  на , в результате чего получим

.

(8.40)

Решение этого уравнения , где В − постоянная интегрирования, которую можно найти из условия равенства Dn=0 в начальный момент времени (t=0). Тогда , и окончательно величину Dn можно представить в виде

.

(8.41)

Подставив (8.41) в (8.34), получим выражение для ионной тепловой поляризуемости

.

(8.42)

Если поле действует в течение длительного времени, то  и устанавливается постоянная поляризация, величина которой определяется соотношением

.

(8.43)

Поляризуемость уменьшается с увеличением температуры, т. к. тепловое движение препятствует упорядоченному распределению ионов.

Видно, что ионная тепловая поляризуемость , имеющая вид (8.43) существенно отличается от ионной поляризуемости  при упругом смещении, определяемой из уравнения (8.20). В случае тепловой поляризации дипольный момент, возникающий при перемещении каждого иона, постоянен и не зависит от напряженности внешнего поля, поэтому ионная тепловая поляризуемость  от напряженности внешнего поля не зависит.
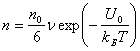
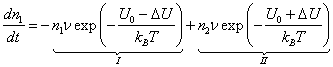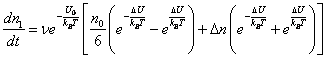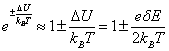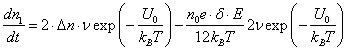