7.3.1. Парамагнетизм электронов проводимости

В металлах вклад в магнитную восприимчивость, кроме атомных остовов, вносят коллективизированные электроны проводимости. При этом магнитное поле оказывает  на них двоякое действие. С одной стороны, поле искривляет траекторию движения свободных электронов, приводя к тому, что они начинают двигаться по спиральной траектории, ось которой совпадает с направлением поля. Такое поведение электронов приводит к диамагнитному отклику, который носит название диамагнетизм Ландау. С другой стороны, каждый электрон, обладая спиновым магнитным моментом, испытывает ориентирующее действие магнитного поля, что приводит к парамагнитному эффекту. Оба этих эффекта имеют квантовый характер.

Л. Д. Ландау теоретически показал, что величина диамагнитного эффекта электронов проводимости в металле втрое меньше величины парамагнитного эффекта, поэтому в целом электронный газ можно считать парамагнитным.

В отсутствии внешнего магнитного поля (B = 0) результирующий магнитный момент электронного газа при температуре абсолютного нуля (T = 0 K) равен нулю. Электроны занимают в зоне проводимости все уровни вплоть до уровня Ферми ( − энергия Ферми),  и на каждом из них, в соответствии с принципом Паули, находятся два электрона с противоположно направленными спинами. Более подробно особенности зонной структуры твердых тел и заполнение электронных состояний в зонах будет рассмотрено в гл. 9.

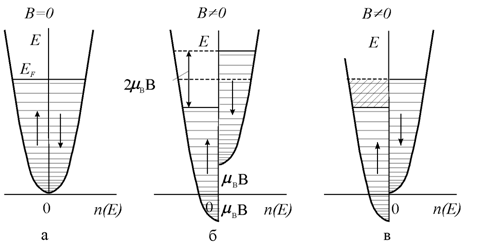
Как показано на рис. 7.7 а, зона проводимости разделяется на две полузоны, различающиеся направлениями спинов электронов.

 

Рис. 7.7. Влияние внешнего магнитного поля на число электронов в двух половинах зоны. (По оси ординат отложена энергия электронов, а по оси абсцисс − плотность электронных состояний. Занятые состояния заштрихованы. Направления спинов в полузонах показаны стрелками.)

 

В магнитном поле () полузона, в которой спиновые магнитные моменты направлены так же, как вектор магнитной индукции , сместится вдоль оси энергии E вниз на величину  ( − магнетон Бора), а полузона со спинами, направленными против поля, на столько же вверх (рис. 7.7, б). Известно, что всякая система стремится к минимуму энергии, отвечающему наиболее устойчивому состоянию. В соответствии с этим часть электронов из правой полузоны перейдет в левую, изменив при этом направление спина (рис. 7.7, в).

Парамагнитная восприимчивость электронного газа  рассчитывается из функции плотности электронных состояний  по формуле

,

(7.26)

где N – число электронов проводимости в единичном объеме, T_F – температура Ферми, которая соответствует заполнению всех уровней вплоть до уровня Ферми  (температуру Ферми называют также температурой вырождения электронного газа). На каждом из уровней находится по два электрона с противоположными спинами. Поскольку ни одна величина в этом выражении не зависит от температуры, то и парамагнитная восприимчивость свободных электронов от температуры не зависит.

Величина рассмотренного эффекта мала. Для типичного одновалентного металла плотность электронных состояний составляет приблизительно  на 1 Дж, отсюда  имеет значение около. Это значение парамагнитной восприимчивости лишь немного больше, чем диамагнитная восприимчивость внутренних заполненных оболочек атомов. Столь малая величина парамагнитной восприимчивости электронного газа связана с тем, что лишь малая часть электронов проводимости, моменты которых были ориентированы противоположно полю, могут осуществить поворот спинов за счет энергии внешнего магнитного поля. Электронный газ в металлах является вырожденным, вследствие чего только незначительная доля электронов в узкой полосе шириной  (рис. 7.7, б) близ уровня Ферми может изменить свое энергетическое состояние. Для остальных электронов такие изменения невозможны, т. к. все соседние энергетические уровни заняты. Можно отметить, что в случае, если бы все валентные электроны реагировали на внешнее поле, парамагнитная восприимчивость того же одновалентного металла была бы в 100 или 1000 раз больше, чем фактически наблюдаемая.