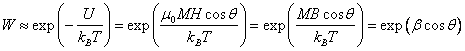7.3. Природа парамагнетизма
Парамагнетизм
− это свойство тела намагничиваться во внешнем поле ![]() в направлении поля, т. е. парамагнитная
восприимчивость
в направлении поля, т. е. парамагнитная
восприимчивость ![]() − величина
положительная. Вследствие этого парамагнетики притягиваются к полюсам
постоянного магнита, тогда как диамагнетики отталкиваются.
− величина
положительная. Вследствие этого парамагнетики притягиваются к полюсам
постоянного магнита, тогда как диамагнетики отталкиваются.
Если полный магнитный момент атома или молекулы в отсутствие внешнего магнитного поля отличен от нуля, то такой атом (или молекула) будет вести себя как элементарный постоянный магнит. Как было сказано выше, полный магнитный момент атома складывается из орбитального и спинового моментов входящих в него электронов. Однако, в силу межатомного взаимодействия, магнитные орбитальные моменты двух спаренных электронов взаимно погашают друг друга. В результате все заполненные электронные оболочки имеют нулевой орбитальный магнитный момент и, следовательно, не могут внести вклад в парамагнитные свойства. Поэтому парамагнетизм обнаруживается только при наличии в атоме неспаренных валентных электронов − электронов проводимости. Спиновые магнитные моменты атомов слабо зависят от влияния поля потенциальных сил связи в кристалле, и поэтому их вклад в магнитный момент атома в твердых телах весьма значителен.
Парамагнитными свойствами обладают:
•
атомы и молекулы, имеющие нечетное число электронов.
Например, щелочные металлы (Na,
K и др.), Al, окись азота (NO). Парамагнитные свойства
проявляют свободные органические радикалы, такие как трифенилметил ![]() . У этих веществ имеется нескомпенсированный спиновый
магнитный момент;
. У этих веществ имеется нескомпенсированный спиновый
магнитный момент;
•
свободные атомы и ионы, имеющие недостроенные
внутренние оболочки (элементы переходных групп, изоэлектронные ионы этих
элементов, редкоземельные металлы и элементы группы актинидов). Примерами могут
служить ионы ![]() ,
, ![]() ,
, ![]() ;
;
• некоторые молекулы с четным числом электронов (O2, S2), органические бирадикалы. В них парамагнетизм вызван нескомпенсированностью спинов двух электронов;
• дефекты кристаллической решетки с нечетным числом электронов (F – центры, вакансии, бивакансии);
• металлы, поскольку они имеют электроны проводимости.
Теория парамагнетизма впервые была создана Ланжевеном.
Пусть в среде,
содержащей N атомов в единице объема,
каждый атом имеет постоянный магнитный момент ![]() , а взаимодействия между магнитными моментами атомов нет. В
отсутствие поля
, а взаимодействия между магнитными моментами атомов нет. В
отсутствие поля ![]() за счет энергии
теплового движения магнитные моменты атомов ориентированы случайным образом и
результирующая намагниченность равна нулю. При наложении внешнего поля все
магнитные моменты ориентируются в направлении поля, но этой ориентации мешает
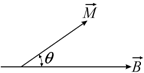
тепловое движение (рис. 7.5).
за счет энергии
теплового движения магнитные моменты атомов ориентированы случайным образом и
результирующая намагниченность равна нулю. При наложении внешнего поля все
магнитные моменты ориентируются в направлении поля, но этой ориентации мешает
тепловое движение (рис. 7.5).
|
|
|
Рис. 7.5. Магнитный момент атома в магнитном поле |
Энергию магнитного диполя в
магнитном поле с индукцией ![]() найдем как
найдем как
|
|
(7.20) |
Эта энергия минимальна, если угол
![]() между векторами
между векторами ![]() равен нулю.
равен нулю.
Вероятность ориентации магнитных моментов атомов под углом ![]() к вектору магнитной
индукции
к вектору магнитной
индукции ![]() в теории Ланжевена
подчиняется распределению Больцмана
в теории Ланжевена
подчиняется распределению Больцмана
|
|
(7.21) |
где ![]() .
.
Тогда среднее значение проекции магнитного момента на направление поля будет
|
|
(7.22) |
где ![]() − функция Ланжевена.
− функция Ланжевена.
Следовательно, результирующая намагниченность, создаваемая N атомами, будет
|
|
(7.23) |
Уравнение (7.23) называется формулой Ланжевена.
При ![]() гиперболический
котангенс в формуле (7.22) можно разложить в ряд и ограничиться двумя первыми
членами разложения, Тогда получим
гиперболический
котангенс в формуле (7.22) можно разложить в ряд и ограничиться двумя первыми
членами разложения, Тогда получим ![]() и намагниченность
можно представить как
и намагниченность
можно представить как
|
|
(7.24) |
а парамагнитную восприимчивость
|
|
(7.25) |
где ![]() − постоянная
Кюри.
− постоянная
Кюри.
Обратно
пропорциональная зависимость парамагнитной восприимчивости ![]() от температуры (7.25)
называется законом Кюри. Однако для
ряда парамагнетиков закон Кюри не выполняется, и имеет место более сложная
зависимость магнитной восприимчивости от температуры.
от температуры (7.25)
называется законом Кюри. Однако для
ряда парамагнетиков закон Кюри не выполняется, и имеет место более сложная
зависимость магнитной восприимчивости от температуры.
Выражения для
намагниченности и парамагнитной восприимчивости (7.24) и (7.25) получены при
условии, что ![]() , а это соответствует слабым полям и нормальным (не очень
низким) температурам. При очень сильных полях и низких температурах
, а это соответствует слабым полям и нормальным (не очень
низким) температурам. При очень сильных полях и низких температурах ![]() и указанные
соотношения перестают быть справедливыми. Если
и указанные
соотношения перестают быть справедливыми. Если ![]() , то
, то ![]() и соответственно
функция Ланжевена
и соответственно
функция Ланжевена ![]() и намагниченность достигает
насыщения
и намагниченность достигает
насыщения ![]() . Это соответствует случаю, когда все магнитные моменты
атомов ориентируются строго в направлении внешнего поля. Экспериментальная
зависимость магнитного момента от отношения величины магнитного поля к температуре
. Это соответствует случаю, когда все магнитные моменты
атомов ориентируются строго в направлении внешнего поля. Экспериментальная
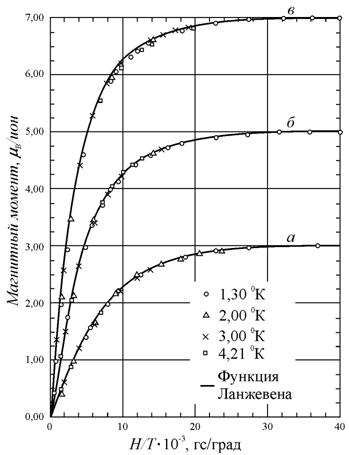
зависимость магнитного момента от отношения величины магнитного поля к температуре
![]() для различных веществ,
показана на рис. 7.6.
для различных веществ,
показана на рис. 7.6.
|
|
|
Рис. 7.6.
Зависимость магнитного момента от отношения |
Выводы теории
парамагнетизма Ланжевена, приводящие к выражению для намагниченности (7.23), а
из него − парамагнитной восприимчивости (7.25), вообще говоря,
противоречат третьему началу термодинамики. Дело в том, что при ![]() энтропия системы
должна тоже стремиться к нулю. Однако вычисление энтропии в рамках классической
теории парамагнетизма Ланжевена приводит к тому, что при стремлении температуры
к абсолютному нулю
энтропия системы
должна тоже стремиться к нулю. Однако вычисление энтропии в рамках классической
теории парамагнетизма Ланжевена приводит к тому, что при стремлении температуры
к абсолютному нулю ![]() . Причина этого противоречия заключается в том, что при
выводе формулы (7.23) не учитывалось пространственное квантование магнитных
моментов. При учете этого условия необходимо принять, что угол
. Причина этого противоречия заключается в том, что при
выводе формулы (7.23) не учитывалось пространственное квантование магнитных
моментов. При учете этого условия необходимо принять, что угол ![]() между векторами
магнитного момента атома
между векторами
магнитного момента атома ![]() и внешнего поля
и внешнего поля ![]() изменяется не
непрерывно, а дискретно. Подробное рассмотрение квантовой теории парамагнетизма
мы здесь не приводим и направляем читателя к соответствующей учебной
литературе, где этот вопрос рассмотрен достаточно подробно.
изменяется не
непрерывно, а дискретно. Подробное рассмотрение квантовой теории парамагнетизма
мы здесь не приводим и направляем читателя к соответствующей учебной
литературе, где этот вопрос рассмотрен достаточно подробно.
Возвращаясь к вышеизложенному, напомним, что парамагнитными свойствами обладают атомы, имеющие неспаренные спины или нескомпенсированные моменты импульса, т. е. атомы с нечетным числом электронов или частично заполненной внутренней электронной оболочкой. Характер заполнения оболочек определяется правилами Хунда. Согласно этим правилам, спины электронов в оболочке всегда складываются так, чтобы дать максимально возможное (с учетом принципа Паули) значение момента количества движения и магнитного момента.