7.2. Влияние магнитного поля на орбитальное движение электрона. Диамагнетизм

Вещества с отрицательной магнитной восприимчивостью æ<0 называются диамагнетиками. Иначе диамагнетизм можно определить как способность вещества намагничиваться во внешнем магнитном поле в направлении, противоположном направлению этого поля.

Диамагнетизм связан с тенденцией электронных зарядов частично экранировать внутреннюю часть тела от внешнего магнитного поля. Согласно правилу Ленца, всякое изменение магнитного потока, пронизывающего электрический контур, индуцирует в контуре ток такого направления, что его магнитный поток будет противодействовать указанному изменению. В цепи без сопротивления, которой может являться, например, сверхпроводящее кольцо или электрон, движущийся по своей орбите в атоме, индуцированный ток сохраняется до тех пор, пока существует поле. Магнитный момент, связанный с индуцированным током, и есть диамагнитный момент.

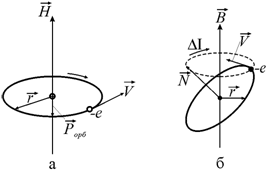
Для вычисления диамагнитной восприимчивости рассмотрим круговую электронную орбиту радиусом r (рис. 7.4, а), плоскость которой перпендикулярна направлению внешнего магнитного поля.

 

Рис. 7.4. Круговая электронная орбита в магнитном поле

 

Электрон в движении вычерчивает своим радиус-вектором круг площадью S. Пусть  − частота вращения электрона, т. е. число оборотов, которое он совершает по орбите за одну секунду, T − период обращения. Орбитальный магнитный момент будет эквивалентен магнитному моменту элементарного кругового тока  и в вакууме (при m =1), с учетом знака заряда электрона он будет равен . Скорость движения электрона по орбите . Тогда изменение орбитального магнитного момента  на некоторую величину  приведет к изменению угловой скорости на  так, что

.

(7.9)

В отсутствии внешнего магнитного поля на электрон действует центробежная сила  (m − масса электрона), уравновешивающая кулоновскую силу взаимодействия электрона с ядром. При наложении на атом магнитного поля, перпендикулярного плоскости орбиты, на электрон будет дополнительно действовать добавочная сила Лоренца . Результирующая центробежная сила приводит к новому значению угловой скорости :

.

(7.10)

Таким образом, используя выражения для сил, получим , или .

Предположим, что при наложении внешнего магнитного поля угловая скорость электрона меняется слабо. Тогда  − малая величина, и можно записать . Следовательно, изменение угловой скорости

.

(7.11)

Из формулы (7.11) следует, что в случае, когда плоскость орбиты электрона перпендикулярна вектору магнитной индукции поля, магнитное поле приводит к изменению угловой скорости движения электрона по орбите, пропорциональному индукции поля. Это изменение не зависит от радиуса орбиты и скорости электрона на ней. В случае, когда направление вращения электрона таково, что орбитальный магнитный момент  направлен в ту же сторону, что и вектор магнитной индукции , действие внешнего магнитного поля сводится к замедлению вращательного движения электрона на величину изменения угловой скорости , определяемую формулой (7.11).

Если орбита наклонена к полю, то под действием поля орбита прецессирует (рис. 7.4, б). Нормаль к плоскости орбиты N описывает конус вокруг вектора магнитной индукции  с постоянной угловой скоростью прецессии , согласно формуле (7.11). Величина  называется частотой Лармора.