Глава 7
МАГНИТНЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
7.1. Классификация магнетиков
Все существующие в природе вещества по своим магнитным свойствам подразделяются на пять видов магнетиков: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики (ферриты). В связи с тем что магнитную активность проявляют все вещества без исключения, можно утверждать, что магнитные свойства веществ определяются элементарными частицами, входящими в состав каждого атома. Такими одинаковыми для всех веществ частицами являются электроны, протоны и нейтроны. Исследования показали, что магнитные моменты протона и нейтрона почти на три порядка ниже наименьшего магнитного момента электрона, поэтому в первом приближении можно пренебречь магнитным моментом ядра, состоящего из протонов и нейтронов, и полагать, что магнитные свойства атома в целом определяются электронами. Это положение является фундаментальным в электронной теории магнетизма, которая общепринята в учении о магнетизме.
Каждый атом
вещества представляет собой динамическую систему, состоящую из ядра и
электронного облака. Каждый электрон обладает определенным спиновым магнитным моментом ![]() и орбитальным магнитным моментом
и орбитальным магнитным моментом ![]() . С некоторой степенью упрощения можно сказать, что спиновый
магнитный момент обусловлен вращением электрона вокруг собственной оси, а
орбитальный − движением электрона по некоторой замкнутой орбите внутри
атома. Следовательно, полный магнитный момент атома будет представлять собой
геометрическую сумму орбитальных и спиновых магнитных моментов электронов,
относящихся к данному атому
. С некоторой степенью упрощения можно сказать, что спиновый
магнитный момент обусловлен вращением электрона вокруг собственной оси, а
орбитальный − движением электрона по некоторой замкнутой орбите внутри
атома. Следовательно, полный магнитный момент атома будет представлять собой
геометрическую сумму орбитальных и спиновых магнитных моментов электронов,
относящихся к данному атому
|
|
(7.1) |
где z − число электронов в атоме.
Рассмотрим макроскопические характеристики твердых тел, связанные с характером взаимодействия магнитных моментов с внешним полем и определяющие принадлежность данного вещества к одному из видов магнетиков [38].
В любом
веществе, внесенном в магнитное поле, возникает суммарный магнитный момент ![]() , который складывается из сумм магнитных моментов
, который складывается из сумм магнитных моментов ![]() , связанных с отдельными частицами (атомами, молекулами).
, связанных с отдельными частицами (атомами, молекулами).
|
|
(7.2) |
Размерность магнитного момента в системе «СИ» − Вольт×секунда×метр [В×с×м] или Вебер×метр [Вб×м].
Одна из основных характеристик магнетиков – их намагниченность
|
|
(7.3) |
Намагниченность j − векторная величина, модуль
которой равен магнитному моменту единицы объема вещества. Намагниченность
растет с ростом индукции магнитного поля ![]() (или напряженности
(или напряженности ![]() ) в соответствии с законом
) в соответствии с законом
|
|
(7.4) |
где ![]() − магнитная постоянная,
− магнитная постоянная, ![]() − относительная магнитная проницаемость,
которая показывает, во сколько раз магнитная индукция поля в данной среде
больше или меньше, чем в вакууме (в вакууме
− относительная магнитная проницаемость,
которая показывает, во сколько раз магнитная индукция поля в данной среде
больше или меньше, чем в вакууме (в вакууме ![]() = 1), æ
− магнитная восприимчивость
вещества, характеризующая способность данного вещества намагничиваться полем
напряженности
= 1), æ
− магнитная восприимчивость
вещества, характеризующая способность данного вещества намагничиваться полем
напряженности ![]() .
.
Величины æ и ![]() являются скалярными, и
магнитная восприимчивость æ для
различных веществ может принимать значения как больше, так и меньше нуля.
Руководствуясь этим свойством, вещества можно разделить на пара-, диа- и
ферромагнетики.
являются скалярными, и
магнитная восприимчивость æ для
различных веществ может принимать значения как больше, так и меньше нуля.
Руководствуясь этим свойством, вещества можно разделить на пара-, диа- и
ферромагнетики.
Если магнитная
восприимчивость принимает положительные значения (æ > 0), то вектор намагниченности (из формулы 7.4) ![]() сонаправлен вектору
напряженности внешнего магнитного поля
сонаправлен вектору
напряженности внешнего магнитного поля ![]() (
(![]() ). Такие вещества относятся к парамагнетикам.
). Такие вещества относятся к парамагнетикам.
Если магнитная
восприимчивость æ < 0, то
векторы намагниченности и напряженности направлены противоположно друг другу (![]() ), что характерно для диамагнетиков.
), что характерно для диамагнетиков.
Как правило,
по абсолютной величине магнитная восприимчивость парамагнетиков больше, чем
диамагнетиков. Зависимость намагниченности этих типов магнетиков от величины
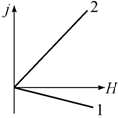
напряженности магнитного поля ![]() линейна (рис. 7.1), и
при отсутствии внешнего поля она равна нулю.
линейна (рис. 7.1), и
при отсутствии внешнего поля она равна нулю.
Интересно, что
линейная зависимость ![]() для парамагнетиков
имеет место только в области слабых полей и высоких температур. В сильных полях
и при низких температурах
для парамагнетиков
имеет место только в области слабых полей и высоких температур. В сильных полях
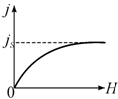
и при низких температурах ![]() выходит на насыщение
выходит на насыщение ![]() (рис. 7.2).
(рис. 7.2).
|
|
|
|
Рис. 7.1. Зависимость намагниченности от напряженности магнитного поля: 1- диамагнетика; 2 - парамагнетика |
Рис. 7.2. Зависимость намагниченности от напряженности магнитного поля в сильных полях и при низких температурах выходит на насыщение |
Кроме
двух рассмотренных видов магнетиков, имеется также достаточно большая группа
веществ, обладающих спонтанной намагниченностью. Они называются
ферромагнетиками и имеют отличную от нуля магнитную восприимчивость (![]() ) даже в отсутствие внешнего поля. Механизм намагничивания
ферромагнетиков оказывается довольно сложным, и полный цикл намагниченности
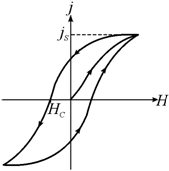
ферромагнетиков описывается петлей
гистерезиса (рис. 7.3).
) даже в отсутствие внешнего поля. Механизм намагничивания
ферромагнетиков оказывается довольно сложным, и полный цикл намагниченности
ферромагнетиков описывается петлей
гистерезиса (рис. 7.3).
В ряде
кристаллов направления вектора магнитной индукции![]() и напряженности магнитного поля
и напряженности магнитного поля ![]() не совпадают. В этом
случае магнитная проницаемость вещества
не совпадают. В этом
случае магнитная проницаемость вещества ![]() является тензорной величиной, т. е. зависит от
направления внутри кристалла. Такие вещества называются магнитно-анизотропными. Мы будем рассматривать здесь только
магнитно-изотропные вещества, для которых магнитная проницаемость
является тензорной величиной, т. е. зависит от
направления внутри кристалла. Такие вещества называются магнитно-анизотропными. Мы будем рассматривать здесь только
магнитно-изотропные вещества, для которых магнитная проницаемость ![]() − простое число.
− простое число.
Найдем связь между магнитной проницаемостью и
восприимчивостью вещества. Величина магнитной индукции ![]() связана с
напряженностью поля
связана с
напряженностью поля ![]() соотношением
соотношением
|
|
(7.5) |
|
|
|
Рис. 7.3. Петля гистерезиса в ферромагнетиках |
Для ферромагнетика
результирующее поле в нем, которое и является магнитной индукцией, можно
определить как
|
|
(7.6) |
поле в ферромагнетике
складывается из напряженности внешнего магнитного поля ![]() и намагниченности
и намагниченности ![]() , создающей внутреннее магнитное поле. Тогда из формул (7.6),
(7.5) и
, создающей внутреннее магнитное поле. Тогда из формул (7.6),
(7.5) и
(7.4) получим
|
|
(7.7) |
Выше было сказано, что
магнитный момент атомов связан с движением электронов относительно своей оси и
их орбитальным движением. Следовательно, существует некая жесткая связь между
механическими и магнитными характеристиками атомов. Эта связь задается так
называемыми гиромагнитными соотношениями.
Обозначим орбитальный механический момент электрона ![]() , а спиновый механический момент электрона
, а спиновый механический момент электрона ![]() . Пользуясь обозначениями магнитных моментов, заданными в
формуле (7.1), запишем гиромагнитные соотношения
. Пользуясь обозначениями магнитных моментов, заданными в
формуле (7.1), запишем гиромагнитные соотношения
|
|
(7.8) |
где е − заряд электрона, а т
− его масса.
Следуя первому постулату
Бора, согласно которому орбитальный момент количества движения электрона ![]() должен быть квантован
и кратен величине
должен быть квантован
и кратен величине ![]() (постоянной Планка,
деленной на 2π), можно сделать
вывод, что квантован и орбитальный магнитный момент
(постоянной Планка,
деленной на 2π), можно сделать
вывод, что квантован и орбитальный магнитный момент ![]() . Элементарный магнитный момент атома с одним электроном,
движущимся по первой орбитали, называется магнетоном
Бора:
. Элементарный магнитный момент атома с одним электроном,
движущимся по первой орбитали, называется магнетоном
Бора:
![]() .
.