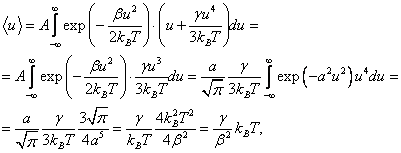6.4. Ангармонизм колебаний атомов и тепловое расширение

При рассмотрении тепловых колебаний в выражении для потенциальной энергии (5.11) мы ограничились лишь второй производной по межатомным расстояниям. В этом (гармоническом) приближении выполняется закон Гука, а тепловое расширение необъяснимо. Кроме того, в гармоническом приближении:

·         равны между собой адиабатические и изотермические упругие постоянные и они не зависят от давления и температуры;

·         теплоемкость при высоких температурах перестает зависеть от температуры и ;

·         упругие волны в решетке не взаимодействуют друг с другом и со временем не изменяют свою форму.

В реальных телах ни одно из этих следствий гармонического приближения точно не выполняется.

Учет производных третьего и более высокого порядков в выражении (5.11) соответствует ангармоническому приближению.

Ангармонизм колебаний атомов приводит к тому, что силовые постоянные, характеризующие величину сил межатомной связи, зависят от амплитуды колебаний, а значит, и частота начинает зависеть от амплитуды смещений. Ангармонизм ведет и к возникновению таких явлений, как тепловое расширение и взаимодействие фононов.

Взаимодействие двух фононов можно, с одной стороны, рассматривать как процесс рассеяния одной волны на периодических неоднородностях, созданных другой волной, с другой - как рассеяние двух частиц при их взаимодействиях друг с другом. В результате взаимодействия фононов с частотами w₁ и w₂ возникает третий фонон с частотой w₁+w₂. Его возникновение происходит в соответствии с законом сохранения энергии и импульса. Трехфононные процессы связаны с кубическими членами разложения потенциальной энергии. Вероятность протекания четырехфононных и более процессов уже много меньше, чем трехфононных. Взаимодействие фононов с передачей энергии от одного к другому фонону возможно только в том случае, когда частотный спектр, являющийся в гармоническом кристалле суммой δ-функций, становится непрерывным в некоторой области вблизи основной частоты w_i, т. е. δ-функции размываются и перекрываются. Чем выше ангармонизм, тем выше перекрывание и тем больше вероятность взаимодействия между фононами, а значит, тем быстрее устанавливается тепловое равновесие. Степень ангармонизма в решетке особенно мала в области низких температур, где и применима фононная модель, поэтому удобно сохранить представление о практически идеальном газе фононов, приписывая каждому фонону эффективное сечение рассеяния. Коэффициент фонон-фононного рассеяния m_ф-ф для модели взаимодействующих фононов, имеющих определенный размер, можно выразить соотношением

 

,

(6.40)

где  − средняя плотность фононов, γ – коэффициент ангармонизма, определяемый величиной кубической производной от потенциальной энергии (6.3) .

 

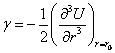Длина свободного пробега фонона l_ф обратно пропорциональна величине коэффициента фонон-фононного рассеяния m_ф-ф. При понижении температуры длина свободного пробега l_ф резко возрастает вследствие сильного уменьшения плотности фононов . Это явление называется эффектом вымораживания фононов, и оно приводит к уменьшению теплоемкости.

С учетом кубического члена в разложении потенциальной энергии взаимодействия атомов в ряд Тейлора (5.11) связан также эффект теплового расширения твердых тел, что приводит к выражению для разности теплоемкостей при постоянном давлении и температуре (6.1).

Обозначим, как было сделано в главе 5, смещение атома из положения равновесия через u, причем , где  − равновесное расстояние между атомами, а r – координата атома в произвольный момент времени.

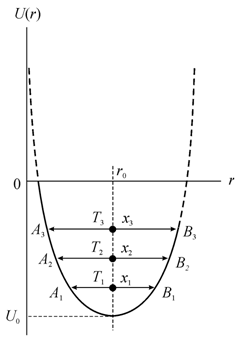
В гармоническом приближении зависимость потенциальной энергии от смещения U(u) − параболическая функция:

,

(6.41)

т. е. атом является гармоническим осцилятором и колеблется в симметричной потенциальной яме (рис. 6.6). При увеличении амплитуды колебаний атом переходит на все более высокие уровни энергии . На каждом возбужденном уровне, соответствующем определенной температуре ( и т. д.), расстояние между ветвями параболы (расстояния , и т. д.) определяет удвоенную амплитуду колебаний. Однако значение  остается постоянным, т. е. среднее положение атома в решетке при гармонических колебаниях не меняется.

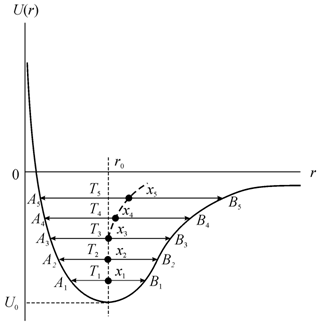
Иначе обстоит дело при учете в разложении потенциальной энергии слагаемого, содержащего куб смещения (). При температуре  атом будет отклоняться так же, как и в случае параболической потенциальной ямы, влево до точки  и вправо до точки  на одинаковые расстояния (рис. 6.7).

 

Рис. 6.6. Зависимость потенциальной энергии взаимодействия между двумя атомами от расстояния между ними в гармоническом приближении (Т1<T2<T3) [74]	Рис. 6.7. Зависимость потенциальной энергии взаимодействия между двумя атомами с учетом ангармонизма колебаний (Т1<T2<T3…) [74]

 

При некоторой достаточно заметной температуре (на рисунке это температуры  и т. д.) отклонения атома от положения равновесия  влево и вправо не равны и средние значения  и т. д. будут отвечать значениям r, отличным от равновесного . Потенциальная энергия при увеличении r меняется медленнее, чем по гармоническому закону, и . Ограничиваясь третьей производной, потенциальную энергию  можно представить в виде

,

(6.42)

где коэффициент . Коэффициент g  в уравнении (6.42) определяет степень отклонения  от параболической зависимости и называется (как указано выше) коэффициентом ангармонизма. Сила, действующая на осциллятор при его отклонении от положения равновесия в ангармоническом приближении, будет иметь вид

.

(6.43)

Таким образом, при увеличении амплитуды колебаний осциллятора с возрастанием температуры происходит увеличение среднего по времени значения его равновесной координаты, т. е. происходит тепловое расширение твердого тела.

Для описания теплового расширения твердого тела можно воспользоваться приближенной моделью, в которой решетка заменена на совокупность ангармонических осцилляторов.

Свяжем коэффициент теплового расширения a (который присутствует в выражении для удлинения тела ) с коэффициентом ангармонизма g. Относительное изменение размера тела при нагревании равно отношению среднего значения отклонения атома от равновесного положения  к значению равновесного расстояния между соседними атомами :

.

(6.44)

Найдем величину среднего значения отклонения атома от положения равновесия

,

(6.45)

где функция f(u) представляет собой вероятность отклонения атома от положения равновесия на величину смещения u. По Больцману эта вероятность равна

,

(6.46)

где А − коэффициент нормировки.

Поскольку g − малая величина, то разложив 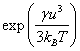 в ряд и ограничиваясь двумя первыми слагаемыми, можно записать

.

(6.47)

Коэффициент нормировки A  в уравнении (6.47) найдем из условия . Тогда

.

(6.48)

Второй интеграл в выражении (6.48) будет равен нулю, поскольку подынтегральная функция нечетная.

Обозначим , тогда, пользуясь табличными значениями интегралов, получим

.

(6.49)

Таким образом,, следовательно, .

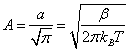Среднее значение отклонения атома от положения равновесия будет равно:

(6.50)

т. к.

Таким образом, среднее смещение атомов от положения равновесия при нагревании пропорционально температуре и коэффициенту ангармонизма g,  и обратно пропорционально квадрату коэффициента квазиупругой силы. Подставив  в формулу (6.44), получим для относительного удлинения тела при нагревании

.

(6.51)

Отсюда

.

(6.52)

Уравнение (6.52) свидетельствует о том, что коэффициент теплового расширения a прямо пропорционален постоянной ангармонизма g, причем знаки их совпадают. Знак a определяется характером асимметрии потенциальной энергии U(r) вблизи положения равновесия. Если ветвь при r<r₀ меняется круче, чем при r>r₀, то при нагревании тело расширяется, если наоборот, то сжимается. Если ветви симметричны, размеры тела не изменяются.

Формула (6.44) справедлива для поликристаллических тел, и a  здесь средний коэффициент линейного теплового расширения. Монокристаллы, как мы уже выяснили в главах 1 и 3, обладают анизотропией свойств, а следовательно, и коэффициент линейного расширения для различных направлений внутри кристалла в общем случае будет иметь различные значения. Если из монокристалла выточить шар, а затем нагреть или охладить его, то при изменении температуры монокристалл потеряет сферическую форму и превратится в трехосный эллипсоид, оси которого связаны с кристаллографическими осями координат кристалла. Коэффициенты теплового расширения по трем кристаллографическим осям называются главными коэффициентами теплового расширения кристалла (они обозначаются буквами ). В табл. 6.3 [78] приводятся главные коэффициенты теплового расширения для некоторых кристаллов, у которых анизотропия выражена особенно ярко.

 

 

Таблица 6.3

Коэффициенты теплового расширения для ряда кристаллов
с сильно выраженной анизотропией

Кристалл	Сингония	Температура, К	, К-1	, К-1	, К-1
Гипс	Моноклинная	313	1,6	42	29
		60	-2		55
Цинк	Гексагональная	150	8		65
		300	13		64
Кальцит	Ромбоэдрическая	313	-5,6		25

 

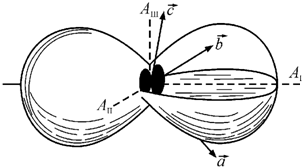
Из табл. 6.3 видно различие в главных коэффициентах расширения у ряда кристаллов весьма значительно, а у некоторых кристаллов (при определенной температуре) наблюдается даже отрицательное значение a. Последнее означает, что такой кристалл при нагревании расширяется по одной из осей и сжимается по двум другим осям. Детальное описание анизотропии теплового расширения кристалла дается фигурами расширения. На рис. 6.8 изображена фигура расширения для кристалла нафталина. Здесь  − оси симметрии фигуры расширения, а  − кристаллографические оси кристалла.

 

Рис. 6.8. Фигура расширения для кристалла нафталина [48]

 

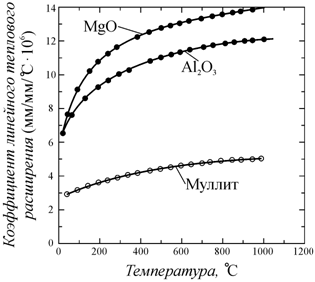
Величина коэффициента теплового расширения в данном направлении соответствует длине радиус-вектора, проведенного из начала координат в этом направлении до границы поверхности фигуры расширения. Значения коэффициента теплового расширения для некоторых металлов приведены в табл. 6.4 [98], а на рис. 6.9 показаны кривые зависимости коэффициента расширения от температуры для трех оксидных соединений.

 

Таблица 6.4

Значения коэффициента линейного теплового расширения

для некоторых металлов

 

Рис. 6.9. Коэффициент линейного теплового расширения как функция температуры для трех оксидов  MgO, Al2O3 и муллита  (3Al2O3 × 2SiO2) [98]

 

Из табл 6.4 и рис. 6.9 видно, что коэффициент теплового расширения металлов и некоторых оксидных соединений уменьшается с уменьшением температуры.
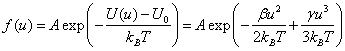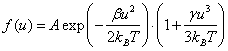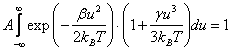