6.3. Электронная теплоемкость и ее зависимость от температуры
В главе 2 при обсуждении природы металлической связи был сделан вывод о том, что при образовании кристаллической решетки металла валентные электроны обобществляются и положительные атомные остатки (ионы) находятся в атмосфере электронного «газа», который и обеспечивает связь в кристалле. При воздействии внешнего электрического поля эти электроны могут создавать поток, называемый электрическим током, поэтому их называют электронами проводимости. При отсутствии поля электроны не прекращают движения, но оно совершается неупорядоченно. С ростом температуры тела вместе с увеличением амплитуды колебаний ионов в решетке должна расти и кинетическая энергия электронов проводимости, а значит, они должны давать вклад в суммарную теплоемкость металла.
Если бы электроны вели себя как классические свободные частицы
идеального газа и каждый из них делал бы вклад в теплоемкость независимо от
остальных, то этот вклад составлял бы ![]() . Если в случае диэлектриков при
. Если в случае диэлектриков при ![]() полная теплоемкость соответствует закону
Дюлонга и Пти, т. е. принимает значение
полная теплоемкость соответствует закону
Дюлонга и Пти, т. е. принимает значение ![]() , то для металлов, в соответствии с вышесказанным, можно
ожидать значения
, то для металлов, в соответствии с вышесказанным, можно
ожидать значения ![]() на моль вещества. В
этом случае теплоемкость вместо значения
на моль вещества. В
этом случае теплоемкость вместо значения ![]() даже в случае простого
одновалентного металла составляла бы значение примерно
даже в случае простого
одновалентного металла составляла бы значение примерно ![]() . Однако эксперименты показали, что в действительности
теплоемкость металлов при высоких температурах мало отличается от теплоемкости
диэлектриков. Следовательно, оценка вклада электронов проводимости в удельную
теплоемкость не может быть проведена на основе классической теории.
. Однако эксперименты показали, что в действительности
теплоемкость металлов при высоких температурах мало отличается от теплоемкости
диэлектриков. Следовательно, оценка вклада электронов проводимости в удельную
теплоемкость не может быть проведена на основе классической теории.
Согласно квантовой теории теплоемкость электронного газа при низких температурах пропорциональна первой степени температуры, т. е. зависит от температуры линейно:
|
|
(6.37) |
где ![]() − масса
электрона.
− масса
электрона.
Численное значение коэффициента ![]() в уравнении (6.37)
обычно составляет около 4×10-4 Дж/(моль×К2), и, следовательно,
при комнатной температуре вклад электронов в полную теплоемкость составляет
примерно 12,6×10-2
Дж/(моль×К).
Эта величина очень мала по сравнению со значением решеточной теплоемкости,
даваемым законом Дюлонга и Пти.
в уравнении (6.37)
обычно составляет около 4×10-4 Дж/(моль×К2), и, следовательно,
при комнатной температуре вклад электронов в полную теплоемкость составляет
примерно 12,6×10-2
Дж/(моль×К).
Эта величина очень мала по сравнению со значением решеточной теплоемкости,
даваемым законом Дюлонга и Пти.
При достаточно низких температурах (обычно ниже 4 К) доля теплоемкости
электронного газа в металлах (![]() ) превышает долю решеточной теплоемкости (
) превышает долю решеточной теплоемкости (![]() ) и становится определяющей. В основе данного вывода лежит
тот факт, что электронная теплоемкость уменьшается с температурой линейно, а
решеточная − по закону
) и становится определяющей. В основе данного вывода лежит
тот факт, что электронная теплоемкость уменьшается с температурой линейно, а
решеточная − по закону ![]() . Это дает возможность для экспериментального
определения коэффициента
. Это дает возможность для экспериментального
определения коэффициента ![]() в формуле (6.37) путем
измерений теплоемкости при очень низких температурах.
в формуле (6.37) путем
измерений теплоемкости при очень низких температурах.
Из изложенного следует, что при температурах много ниже ![]() полная теплоемкость
металла может быть представлена в виде
полная теплоемкость
металла может быть представлена в виде
|
|
(6.38) |
где коэффициент a − постоянная величина.
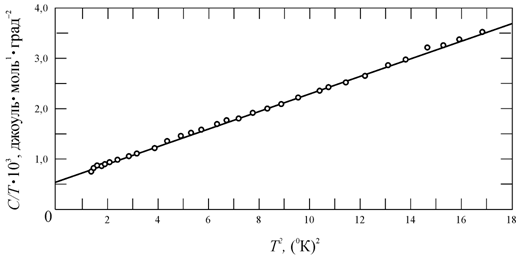
Если представить формулу (6.38) в виде
|
|
(6.39) |
то график
зависимости ![]() от
от ![]() будет представлять
собой прямую (рис. 6.5), причем пересечение этой прямой с осью ординат даст значение
коэффициента g, а наклон прямой −
величину a.
будет представлять
собой прямую (рис. 6.5), причем пересечение этой прямой с осью ординат даст значение
коэффициента g, а наклон прямой −
величину a.
|
|
|
Рис. 6.5.
Зависимость |
Определив значение a,
по формуле (6.39) можно вычислить характеристическую температуру Дебая ![]() .
.
Как уже было сказано выше, при низких температурах теплоемкость,
обусловленная электронами, больше теплоемкости решетки, а при высоких −
значительно меньше. Однако при достаточно высоких температурах электронная
теплоемкость может вновь стать весьма значительной, т. к. теплоемкость решетки,
достигнув ![]() , при дальнейшем увеличении температуры (выше температуры
Дебая
, при дальнейшем увеличении температуры (выше температуры
Дебая ![]() ) уже не увеличивается. Большинство металлов плавится до
того, как электронная теплоемкость достигнет заметной величины, однако именно
электронная теплоемкость ответственна за медленное линейное возрастание полной
теплоемкости (рис. 6.1) при высоких температурах, в то время как решеточная
теплоемкость в этой области температур уже практически не меняется.
) уже не увеличивается. Большинство металлов плавится до
того, как электронная теплоемкость достигнет заметной величины, однако именно
электронная теплоемкость ответственна за медленное линейное возрастание полной
теплоемкости (рис. 6.1) при высоких температурах, в то время как решеточная
теплоемкость в этой области температур уже практически не меняется.
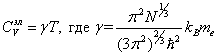 ,
,