3.3.1. Образование дислокаций в кристалле
Чтобы в идеальном кристалле
образовалась дислокация, необходимо произвести сдвиг в некоторой части
плоскости скольжения. Для этого нужно приложить силу. В реальности рассчитывается
не сила, а величина 
– прочность сдвига в совершенном
кристалле, или скалывающее напряжение.
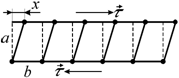
Рассмотрим прямоугольную решетку (рис. 3.16) [74]. Пусть x – смещение, соответствующее приложенному напряжению t. При смещении одной атомной цепочки относительно другой в решетке возникают препятствующие смещению напряжения t. Эти напряжения стремятся восстановить нарушенное равновесие.
|
|
|
Рис. 3.16. Сдвиг прямоугольной решетки |
В силу
симметрии решетки 
, если 
, где 
. Решетка оказывает сопротивление приложенному напряжению 
при 
и 
, если 
.
Этим условиям удовлетворяет синусоидальный закон:
|
|
(3.14) |
,где k – постоянная величина.
Величина
коэффициента k определяется из закона
Гука. При малых смещениях 
, поэтому
|
|
(3.15) |
С другой стороны, для малых смещений выполняется закон Гука:
|
|
(3.16) |
где G – модуль сдвига. Поэтому можно записать
|
|
(3.17) |
.Отсюда
|
|
(3.18) |
.Максимальное
сопротивление сдвигу, как следует из выражения (3.14), возникает при 
. Следовательно, коэффициент k есть не что иное, как максимальное сопротивление сдвигу. Эту
величину принимают за теоретическую прочность кристалла на сдвиг:
|
|
(3.19) |
.Для
кристаллов, в которых отношение периодов решетки b/a составляет
около 0,6 критическое скалывающее напряжение, рассчитанное по формуле
(3.19), должно составлять 
. Теоретическое
число, полученное при учете межатомных взаимодействий в плоскости скольжения,
дает несколько меньшее значение 
. Вместе с тем, экспериментальные измерения показывают, что
сдвиг в большинстве реальных кристаллов начинается при значительно меньших
напряжениях 
. Это связано с тем, что сдвиг в кристаллах происходит
не путем смещения одних атомных плоскостей относительно других, а путем
скольжения дислокаций, имеющихся в кристалле. Часто дислокации в кристалле
появляются уже на стадии его роста. Получить кристаллы, не содержащие
дислокации, очень сложно. Даже в совершенных кристаллах их плотность (число
дислокаций, пересекающих единичную площадку внутри кристалла) достигает 
, а в сильно деформированных металлических кристаллах может
достигать 
. В настоящее время существуют методы получения
бездислокационных кристаллов. Измерение прочности таких кристаллов показывает,
что она близка к теоретической.
Источники дислокаций
При деформации плотность дислокаций в кристаллах способна возрастать на несколько порядков (от 102 до 1012 1/см2). Для объяснения этого явления надо допустить, что внутри кристалла имеются некие источники дислокаций.
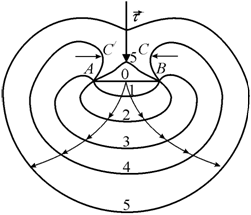
Механизм одного из таких источников был предложен Франком и Ридом (рис. 3.17).
|
|
|
Рис. 3.17. Источник дислокаций Франка−Рида [112]
|
Линия АВ
представляет собой дислокацию с закрепленными концами (положение 0). Под
действием внешнего механического напряжения 
дислокация начинает
выгибаться в плоскости скольжения и занимает положение 1. Постепенное выгибание
дислокации может происходить только при непрерывно возрастающем напряжении,
которое достигает максимума, когда дислокация принимает форму полуокружности.
При этом критическое напряжение
|
|
(3.20) |
,где L – длина отрезка АВ.
При внешних механических напряжениях 
конфигурация
становится нестабильной и дислокация расширяется самопроизвольно,
последовательно занимая положения 2, 3, 4.
В положении 4 части дислокационной петли С и С/ имеют винтовые компоненты противоположного знака, т. е. они движутся навстречу друг другу и взаимно уничтожаются. В результате происходит разделение дислокации на внешнюю и внутреннюю (5). Теоретически число дислокаций, возникающих от источника Франка−Рида, может быть бесконечным, но на практике это число увеличивается до тех пор, пока взаимодействие упругих полей дислокаций не сбалансирует критическое напряжение сдвига. После этого источник становится неактивным.
Бардин и Херинг предложили другой механизм генерации дислокаций, который отчасти аналогичен источнику Франка−Рида. В этом случае движение дислокации происходит за счет зарождения или поглощения вакансий, поэтому действие такого источника зависит от концентрации последних.
Кроме этих двух видов источников дислокаций, существуют и другие модели.