3.3.2. Движение дислокаций

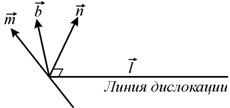
Дислокации могут сравнительно легко передвигаться через кристалл. Предположим, что дислокация с единичным вектором оси дислокации  и вектором Бюргерса  передвигается в плоскости с нормалью  (рис. 3.18) (положительное направление нормали выбирается произвольно). Тогда скалярное произведение векторов .

Пусть  − единичный вектор направления движения дислокации, который определяется из соотношения

 

.

(3.21)

Пусть положительная сторона плоскости скольжения связана с направлением вектора , другую сторону плоскости назовем отрицательной. Когда дислокация движется по плоскости в направление , часть кристалла, расположенная с положительной стороны плоскости, сдвигается на вектор  относительно части кристалла, находящейся с отрицательной стороны. Рассмотрим два случая.

1.      Пусть вектор  лежит в плоскости перемещения дислокации, т. е.

.

(3.22)

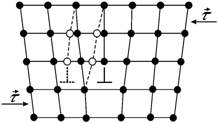
Такое движение дислокации называют скольжением, а плоскость движения – плоскостью скольжения (рис. 3.19). Скольжение осуществляется за счет незначительной перестройки атомов вблизи линии дислокации. Скольжение дислокации не сопровождается переносом массы и происходит под действием небольших касательных напряжений t.

 

 

Рис. 3.18. К выводу движения дислокации	Рис. 3.19. Перемещение дислокации на одно межатомное расстояние

 

Расчет показывает, что для того, чтобы заставить скользить дислокацию требуется механическое напряжение , что по порядку величины совпадает с критическим напряжением, при котором развивается пластическая деформация кристаллов. Это приводит к выводу, что пластическая деформация кристаллов связана с движением дислокаций.

Если вектор Бюргерса  параллелен вектору , т. е. дислокация винтовая, то любой вектор , для которого , также удовлетворяет условию (3.22). Таким образом, любое движение винтовой дислокации является скольжением. При этом плоскость скольжения неопределенна и может быть любой из плоскостей, осью которой служит линия дислокации.

2.      Другой случай − вектор  не лежит в плоскости скольжения, т. е.

.

(3.23)

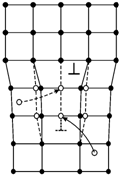
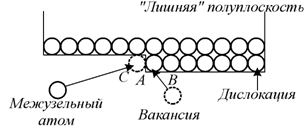
Это означает, что краевая дислокация смещается в направлении, перпендикулярном плоскости скольжения, когда происходит «наращивание» или «растворение» атомных рядов на краю «лишней» полуплоскости. В этом случае дислокация оставляет за собой либо вакансии, либо междоузельные атомы. Движение сопровождается переносом вещества. Такое движение называется переползанием дислокации (рис. 3.20).

 

Рис. 3.20. Переползание дислокации за счет поглощения межузельных атомов

 

Переползание дислокаций происходит обычно при больших температурах и больших временах выдержки под нагрузкой, когда велика диффузионная подвижность атомов.

 

Развитие дислокационной пластичности кристалла определяется подвижностью дислокаций и интенсивностью их зарождения. Подвижность изолированной дислокации в предельно чистом монокристалле зависит от характера сил межатомных связей, взаимодействия дислокаций с частицами в кристалле. Подвижность дислокаций в неидеальных кристаллах уменьшается за счет их взаимодействия друг с другом и с другими дефектами. Такое взаимодействие приводит к торможению или даже стопорению движущихся дислокаций. Осевшие на дислокации примеси блокируют ее движение, как бы «пришпиливая» в некоторых точках линию дислокации. Отрыв дислокации от примесей, т. е. преодоления препятствий («стопоров дислокации»), мешающих ее движению, при высоких температурах происходит за счет термоактивации. При низких температурах эти процессы затруднены, но все же возможны за счет квантового туннелирования дислокации.

Взаимодействие дислокаций с точечными дефектами

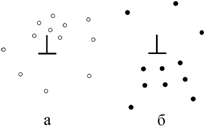
В реальных кристаллах присутствуют и дислокации, и точечные дефекты. Междоузельный атом является в решетке центром напряжения сжатия, а вакансия вызывает растяжение. Эти дефекты соседствуют с дислокациями, и между ними и дислокациями возникает упругое взаимодействие. В области растяжения возникает повышенная концентрация междоузельных атомов и пониженная концентрация вакансий, а в области сжатия наоборот повышенная концентрация вакансий и пониженная – междоузельных атомов (рис. 3.21).

Если в кристалле имеются примесные атомы, то между ними и краевыми дислокациями тоже существует взаимодействие. Атомы, внедренные в решетку, занимают либо положения замещения, заменяя атомы исходного вещества в узлах решетки, либо внедряются в междоузлия. Примесь в каждом из этих случаев является центром расширения или сжатия. Это приводит к тому, что инородные атомы притягиваются дислокацией и располагаются вокруг нее. Говорят, что вокруг дислокаций образуется атмосфера примесных атомов («шуба»).

В большинстве реальных кристаллов вследствие их анизотропии искажения, вносимые дефектами, являются несимметричными. Это ведет к их взаимодействию со скалывающими напряжениями вокруг винтовой дислокации.

Краевая дислокация, переходящая из одной плоскости скольжения в другую, расположенную выше на одно межатомное расстояние, называется ступенькой. Если расстояние между плоскостями скольжения равно одному периоду решетки, то дислокационную ступеньку называют единичной, в случае более удаленных друг от друга плоскостей скольжения ее называют сверхступенькой.

Точечные дефекты могут аннигилировать на дислокации. Если к точке А единичной дислокационной ступеньки (рис. 3.22) подходит вакансия, то ступенька смещается в положение В, а сама вакансия исчезает. Если же к точке А подходит межузельный атом, то процесс аналогичен и ступенька смещается в С с поглощением межузельного атома.

 

 

Рис. 3.21. Распределение точечных дефектов вокруг краевой дислокации: а - вакансий; б - межузельных атомов	Рис. 3.22. Аннигиляция точечных дефектов на ступеньке краевой дислокации

 

Кроме упругого взаимодействия дефектов в большинстве твердых тел осуществляется также электрическое взаимодействие. Наиболее ярко оно проявляется в полупроводниках и диэлектрических ионных кристаллах. Оборванные связи в области дислокации действуют как акцепторы. В полупроводниках n-типа они могут захватывать электроны проводимости и тем самым создают кулоновское взаимодействие дислокации и положительного иона. Максимальная величина электрического взаимодействия может быть представлена приближенным выражением

,

(3.24)

где f − доля свободных оборванных связей, a − расстояние между этими связями, e − заряд электрона. При комнатной температуре максимальное значение .

Барьеры Пайерлса

Важной характеристикой материала, связанной с движением дислокаций, являются так называемые напряжения (или барьеры) Пайерлса [78, 112]. Рассмотрим изменение сил, действующих на дислокацию при ее перемещении на вектор Бюргерса (рис. 3.23). В исходном положении силы отталкивания, действующие на дислокацию со стороны соседних плоскостей, одинаковы и симметрично направлены в противоположные стороны. 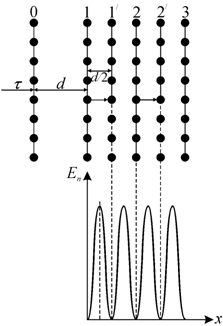С началом перемещения дислокации из исходного положения 1 напряжение отталкивания увеличивается и достигает максимума, пройдя путь d/4, где d − межплоскостное расстояние, и затем изменяется до минимума под влиянием сил притяжения при переходе в положение , равное d/2. Процесс повторяется при переходе из положения  в положение 2. При этом полуплоскость 2 сместится вправо в положение . Такое циклическое изменение напряжения происходит в течение всего времени движения дислокации.

 

Рис. 3.23. Перемещение дислокации в решетке и периодический характер изменения при этом ее потенциальной энергии [78]

 

Следовательно, при перемещении дислокации в решетке она испытывает периодическое изменение тормозящих упругих напряжений. Это происходит так, как будто дислокация тормозится силами трения в решетке. Положение, соответствующее , называют долиной потенциального рельефа. Характер зависимости потенциальной энергии краевой дислокации  от смещения из равновесного положения определяется типом химической связи и другими факторами. В первом приближении ее считают синусоидальной и определяют из формулы

,

(3.25)

где m − коэффициент Пуассона, G − модуль упругости, b − модуль вектора Бюргерса, равный трансляционному вектору в направлении перемещения дислокации, x − текущая координата, a − ближайшее межатомное расстояние в направлении движения дислокации.

Максимальное (амплитудное) значение  и есть барьер Пайерлса , впервые установившего это явление и зависимость (3.24). Чем меньше барьер Пайерлса , тем меньшая энергия необходима для движения дислокации. Для того чтобы дислокация продвигалась в своей системе скольжения, фактически приложенное напряжение  должно быть больше напряжения Пайерлса . Это означает, что при приложении к кристаллу (кристаллиту) сдвигового напряжения пластическая деформация начнется раньше в той системе скольжения, в которой раньше, чем в других,  окажется выше напряжения Пайерлса.