3.3   Дислокации

К линейным несовершенствам в кристаллах, как уже говорилось выше, относятся дислокации: нарушения регулярности решетки вдоль линии, представляющие собой линейные искажения типа обрыва или сдвига атомных слоев, нарушающие правильность их чередования. Поперечные размеры линейного дефекта не превышают одного или нескольких межатомных расстояний, а длина может достигать размеров кристалла. Понятие о дислокации было введено в 40-е годы XX в. Френкелем и Тейлором для объяснения механизма процесса пластической деформации.

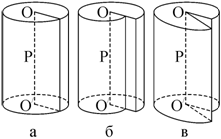
Линейную дислокацию удобно рассмотреть на примере однородного изотропного (например, резинового) упругого цилиндра (рис. 3.9).

 

Рис. 3.9. Образование линии дислокации в упругом однородном цилиндре

 

Разрежем цилиндр вдоль плоскости P (рис. 3.9, а), сместим края так, как показано на рис. 3.9, б и в, и склеим. Линия ОО^/, определяющая область, в которой сдвиг произошел от области, где сдвига нет (рис. 3.9, в), получила название дислокации.

В отличие от рассмотренного примера, кристалл имеет дискретное строение и в общем случае анизотропен, поэтому накладываются ограничения на характер возможных смещений. Допускаются только те смещения, которые соответствуют свойствам симметрии кристаллической решетки.

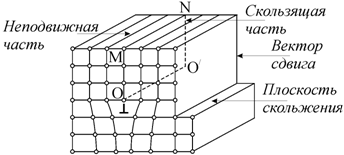
Рассмотрим сдвиговую дислокацию. На n+1 атомных плоскостей выше плоскости скольжения приходится n плоскостей ниже плоскости скольжения. Дислокация ОО^/ (или ось дислокации) представляет собой край полуплоскости MNO^/O и получила название краевой (рис. 3.10). Краевая дислокация перпендикулярна вектору сдвига. Если «лишняя» полуплоскость находится в верхней части кристалла, то дислокацию называют положительной и обозначают значком ^, если в нижней части − отрицательной и обозначают . Область вблизи оси дислокации, составляющая 3−4 межатомных расстояния, представляющая собой некую трубку вокруг линии дислокации, называют ядром дислокации.

Приложение напряжения сдвига приводит к перемещению краевой дислокации, причем смещение ее оси ОО^/ на одну трансляцию означает смену полуплоскости, образующей в данный момент дислокацию. Перемещение краевой дислокации через весь кристалл приведет к сдвигу части кристалла на одно межатомное расстояние. Результатом этого является пластическая деформация кристалла (рис. 3.11), т. е. части кристалла оказываются смещены друг относительно друга на одну трансляцию.

 

Рис. 3.10. Краевая дислокация ОО/, возникшая в результате сдвига

Рис. 3.11. Пластическая деформация как результат движения краевой дислокации под действием напряжения сдвига t  [52]

 

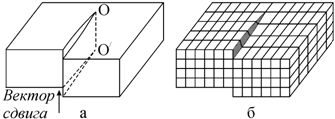
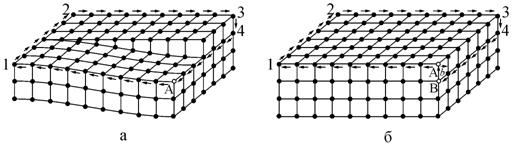
Еще одним типом линейных дефектов являются винтовые дислокации. Бюргерсом было дано представление о винтовой дислокации. Пусть в кристалле произведен такой сдвиг, при котором линия дислокации ОО^/ (рис. 3.12, а), отделяющая область, где он произошел, от области, где сдвига нет, параллельна вектору сдвига. В этом случае кристалл можно представить в виде атомной плоскости, «закрученной» вокруг оси дислокации ОО^/ винтом. Такая дислокация названа винтовой (рис. 3.12, б).

 

 

Рис. 3.12. Винтовая дислокация

 

 

Возможен случай, когда дислокация представляет собой кривую. Такие дислокации называются смешанными (рис. 3.13). В точке О дислокация винтовая, а в точке О^/ − краевая.

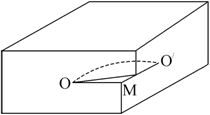
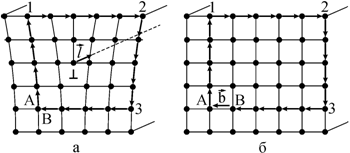
Важными характеристиками дислокации являются вектор Бюргерса и контур Бюргерса. Назовем областью хорошего кристалла любую область реального кристалла, где можно установить однозначное соответствие с идеальным кристаллом, а где такого соответствия установить нельзя, – областью плохого кристалла. Контуром Бюргерса (рис. 3.14) называют замкнутый контур произвольной формы, построенный в реальном кристалле так, что от атома к атому переходят последовательно, не выходя из области хорошего кристалла.

 

Рис. 3.13. Смешанная дислокация	Рис. 3.14. Построение контура Бюргерса: а − в реальном; б − исходном идеальном кристалле

 

Если в реальном кристалле контур проведен вокруг дислокации, то соответствующий контур в идеальном кристалле окажется разомкнутым (рис. 3.14, б). Чтобы замкнуть контур, его надо дополнить вектором , который и является вектором Бюргерса. Направление вектора  определяется следующими условиями:

 

•         если положительное направление дислокации выбрано произвольно, то обход контура Бюргерса определяется по правилу правого винта;

•         вектор Бюргерса направлен от конечной точки В к начальной точке А.

 

В случае краевой дислокации вектор Бюргерса  перпендикулярен линии дислокации (рис. 3.14), а для винтовой − параллелен ей (рис. 3.15).

 

 

 

Рис. 3.15. Контур и вектор Бюргерса винтовой дислокации: а − реальный; б − идеальный кристалл

 

Таким образом, и винтовая, и краевая дислокации − это граница между сдвинутой и несдвинутой частями кристалла (область незавершенного сдвига) или нарушение правильности структуры вдоль некоторой линии, которая не может оборваться внутри кристалла. Линия дислокации должна либо выходить на поверхность кристалла, либо разветвляться на другие дислокации, либо образовывать внутри кристалла замкнутые петли или взаимосвязанную сетку. Именно последняя возможность чаще всего реализуется в кристаллах.

Вектор Бюргерса для контура, замыкающегося вокруг нескольких дислокаций, равен сумме векторов Бюргерса отдельных дислокаций. Если дислокация с вектором Бюргерса  разделяется внутри кристалла на несколько дислокаций с векторами Бюргерса , ,…, , то выполняется условие .

Вектор Бюргерса всегда является одним из векторов трансляции решетки, поэтому его модуль и направление ограничены рядом дискретных значений, определяемых структурой кристалла.

Следует заметить, что для точечных дефектов, рассмотренных выше, вектор Бюргерса равен нулю.