10.8. Кинетическое уравнение Больцмана

Более строго отклик электронного газа в твердом теле на внешние воздействия рассматривается в рамках квантовой теории. При внешних воздействиях функция распределения электронов по энергиям становится неравновесной. В рамках квантовой теории изменение функции распределения электронов описывается следующим уравнением, называемым кинетическим уравнением Больцмана:

.

(10.53)

В уравнении (10.53) учтено изменение числа электронов в фазовом пространстве за счет диффузии, действия внешних сил и процессов рассеяния. Левая часть уравнения отражает изменение функции распределения во времени. Первое и второе слагаемое правой части характеризуют изменение функции распределения под действием внешних полей, изменяющих состояние электронов в координатном пространстве и пространстве волновых векторов. Эту часть называют полевым членом уравнения Больцмана, и она имеет вид

.

(10.54)

Изменение функции распределения электронов по состояниям в k-пространстве в результате рассеяния электронов описывается в кинетическом уравнении последним слагаемым, называемым интегралом столкновения:

.

(10.55)

С учетом соотношений (10.53, 10.54) кинетическое уравнение Больцмана можно записать следующим образом:

.

(10.56)

В случае слабого электрического поля полевой член в кинетическом уравнении Больцмана (10.54) можно представить в следующем виде:

.

(10.57)

Поскольку производная от квазиимпульса p_x по времени равняется внешней силе

,

(10.58)

то для полевого члена получаем

.

(10.59)

Используя критерий малости возмущения, представим неравновесную функцию распределения в виде равновесной функции f₀ и малой добавки f₁.

.

(10.60)

В случае слабого возмущения скорость изменения неравновесной  функции распределения будет пропорциональна величине возмущения.

,

(10.61)

где τ − время релаксации.

Решение уравнения (10.61) имеет классический вид, описываемый соотношением

.

(10.62)

Здесь есть значение добавки к неравновесной функции распределения  в момент t = 0, т. е. в момент выключения поля.

Для стационарного состояния, когда изменение функции распределения за счет внешних сил уравновешивается соударениями (рассеиваниями)

.

(10.63)

С учетом уравнений 10.62, 10.61 и 10.60 получаем для неравновесной функции распределения

.

(10.64)

С учетом слабости возмущения, т. е. малого отличия равновесной и неравновесной функций распределения, уравнение 10.64 можно переписать в виде:

,

(10.65)

где  − проекция скорости электрона на ось x.

Переходя от дифференцирования по скорости к дифференцированию по энергии, получаем зависимость функции распределения электронов по состояниям под действием слабого электрического поля

.

(10.66)

Указанное уравнение является одним из вариантов записи кинетического уравнения Больцмана для газа свободных электронов твердых тел.
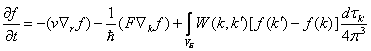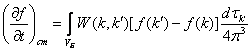