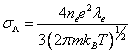10.7. Классическая теория свободных электронов Друде−Лоренца

Некоторые аспекты поведения металлов были объяснены с помощью моделей, основанных на классическом распределении скоростей свободных электронов [94].

Согласно Больцману, число электронов в единице объема, скорости которых в термодинамическом равновесии находятся в интервале  с центром в точке , составляет

,

(10.37)

где n_e – число электронов в единице объема; f₀ – равновесная функция распределения.

Равновесное распределение Больцмана сферически симметрично в пространстве скоростей, и вероятность того, что средняя скорость лежит в интервале от  до , равна

(10.38)

независимо от направления этой скорости.

Средняя кинетическая энергия, приходящаяся на 1 электрон:

,

(10.39)

где  − среднеквадратичная скорость электрона.

Значит,

и .

(10.40)

При нормальных температурах  10⁸ м/с.

При построении классической теории предполагается, что средняя длина свободного пробега электрона определяется в первую очередь упругими столкновениями его с положительными ионными остовами. Если в кристалле в единице объема содержится N_i ионных остовов, причем эффективный радиус их составляет R_i, то средняя длина свободного пробега _e должна иметь порядок _e  ( R_i²N_i)^-1, независимо от скорости электрона.

Среднее время свободного пробега определяется как 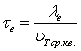, где  – тепловая скорость, с которой электрон движется от одного рассеивающего центра к другому. Любое внешнее поле должно влиять на изменение скорости электронов в течение коротких промежутков времени, сравнимых с τ_e.

Первая классическая модель газа свободных электронов в металле была построена Друде в 1900 году. Несмотря на ограниченность этой модели, она содержит некоторые идеи, остающиеся до сих пор важной частью более точных моделей. В ней предполагается:

1. Все электроны движутся с одинаковыми среднеквадратичными скоростями, определяемыми распределением Больцмана:

.

(10.41)

2. Движущиеся электроны рассеиваются в результате беспорядочных соударений с атомными остовами. После любого соударения скорость равна нулю, т. е. любая (в том числе дрейфовая) скорость уничтожается в результате столкновения.

3. В промежутках между соударениями поле может изменять скорость движения электронов на любую величину, но результат действия поля ликвидируется при соударении.

Найдем величину электропроводности. Пусть имеется группа из n₀ электронов в момент времени t = 0. Число электронов, не испытавших соударение к моменту времени t, равно

.

(10.42)

Скорость уменьшения числа электронов, не испытавших соударение, равна

.

(10.43)

При наложении электрического поля  электрон, не испытавший соударение в течение времени t, приобретает в дополнение к своей тепловой скорости дрейфовую скорость

(10.44)

(т. к. ).

Следовательно, расстояние, которое электрон проходит в направлении поля, будет

(10.45)

(из ).

Этот дрейф накладывается на беспорядочное тепловое движение. Суммарное перемещение за один свободный пробег n₀ электронов равно

.

(10.46)

Такой путь прошли бы n₀ электронов за одинаковое время _е с одинаковой дрейфовой скоростью

.

(10.47)

Если в одном кубическом метре металла содержится n_e электронов, которые в поле  имеют одну и ту же скорость дрейфа , то плотность электрического тока будет

,

(10.48)

где  − электропроводность.

Электропроводность можно выразить и через величину  − дрейфовую подвижность электронов

.

(10.49)

Физический смысл величины   скорость электронов, приобретаемая ими в электрическом поле с единичной напряженностью. Электропроводность  связана с длиной свободного пробега _е выражением

.

(10.50)

Лоренц отказался от упрощения, приписывающего всем электронам одинаковую скорость. Он рассматривал модифицированное распределение Больцмана в присутствии электрического или теплового градиентов. Эти факторы должны приводить как к смещению, так и к искажению равновесной функции распределения f₀. Результирующая формула для электропроводности  в этом приближении

(10.51)

, то есть .

Таким образом, в модели Лоренца электропроводность  изменяется обратно пропорционально , в то время как в экспериментах проявляется обратно пропорциональная зависимость электропроводности от температуры   T^-1.

Кроме того, в модели Друде (Лоренца) энергия каждого электрона равна , а, следовательно, полная кинетическая энергия электронного газа . Тогда вклад электронов в удельную теплоемкость должен быть равен  и . В таком металле, как Na, число свободных электронов равно числу атомов, т. е. электроны должны увеличивать удельную теплоемкость на 50 %, чего в реальности не наблюдается: экспериментально определяемая электронная теплоемкость в металлах очень мала и линейно меняется с температурой. Это еще одно слабое место классической модели Друде.

Электронная теплопроводность в модели Друде равна

.

(10.52)

Тогда число Лоренца . Эта величина находится в хорошем согласии с экспериментальной при комнатной температуре. Расчет _e, , _e по формулам Друде при T = 77 K дает соответственно величины 20 10^-14,  10⁷см/с и 10 Å. Полученные значения достаточно хорошо согласовывались с экспериментом во времена Друде и Лоренца. Однако, когда были получены особо совершенные кристаллы, расчет длины свободного пробега  _e при низких температурах дал значение 1 см (из экспериментальных значений электропроводности), которое невозможно было объяснить.
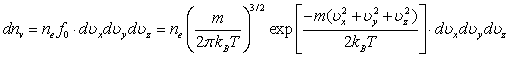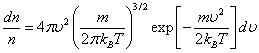
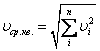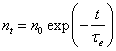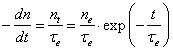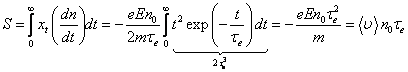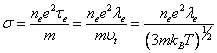