10.2.1. Плотность состояний в двумерной подзоне

Согласно принципу Паули и соотношению неопределенности Δp·Δx ≥ h требуется, чтобы элементарная ячейка фазового пространства Δp_x·Δx·Δp_y·Δy = (2πħ)² содержала не больше двух электронов. В фазовом пространстве объем элементарной ячейки V_ЭЯ = Δk_x·Δx·Δk_y·Δy = 4π².

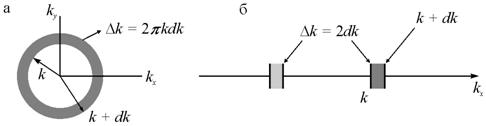
Рассмотрим фазовый объем V_Ф слоя в интервале от k до k+Δk (рис. 10.3). Для удобства дальнейших выкладок перейдем от конечных приращений к дифференциалам. Фазовый объем будет равен V_Ф = 2πkdk.

 

а	б
Рис. 10.3. Изоэнергетическая поверхность для расчета плотности: а - 2D и б - 1D квантовых состояний

 

Тогда число электронов dn, находящихся в этом фазовом объеме, будет с учетом принципа Паули

.

Учитывая квадратичный закон дисперсии E(k), для плотности состояний N(E) в двумерной подзоне из формулы (10.6) получаем

.

(10.7)

Выражение (10.7) соответствует числу состояний на единичный энергетический интервал и на ед. площади ОПЗ толщиной λ_c, в которой локализован электрон. Чтобы получить плотность состояний N(E) на ед. объема, для сравнения с объемной плотностью состояний, выражение (10.8) необходимо разделить на характерный размер λ_c локализации волновой функции в направлении z.

.

Из этого уравнения следует, что следствием двумеризации электрона является независимость плотности состояния от энергии электрона в пределах одной квантовой подзоны. Напомним, что в трехмерном случае плотность состояний N(E) пропорциональна корню квадратному из энергии . При переходе от одной подзоны к другой меняется величина локализации волновой функции λ, а следовательно, и плотность состояний N(E).

 

Квантовый эффект Холла для 2D электронов в сильном магнитном поле

Двумерный электронный газ реализуется в инверсионных слоях МДП-транзисторов, на границе раздела гетеропереходов. Наиболее ярко двумеризация электронного газа проявляется в квантовом эффекте Холла. Эффектом Холла называют появление поперечной разности потенциалов при протекании  электрического тока в твердых телах при наличии магнитного поля, перпендикулярного к плоскости протекания тока. При исследовании эффекта Холла измеряемыми величинами являются холловское напряжение V_H и ток канала I. Если разделить холловское напряжение V_H на ток канала I, то полученная величина имеет размерность сопротивления, обычно называемого холловским сопротивлением R_xy [53].           

.

(10.8)

Для слабых магнитных полей B без учета квантования по магнитному полю B зависимость холловского сопротивления R_xy от плотности электронов Γ_n гиперболическая и гладкая функция.

В случаях сильного магнитного поля B, перпендикулярного плоскости 2D электронного газа, происходит квантование энергии. Величина кванта энергии  будет равна , а возникший дискретный энергетический спектр определяется соотношением . Эти энергетические уровни получили название уровней Ландау.

С учетом квантования по магнитному полю B зависимость холловского сопротивления R_xy будет

                                               .          

Из этого уравнения  следует, что в случае полного заполнения i-го уровня Ландау (ε = 1) величина холловского сопротивления равна:         

.

(10.9)

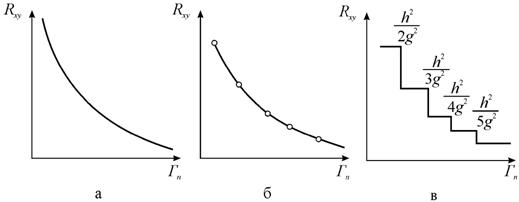
Отметим, что состояния полного заполнения i-го уровня Ландау по оси плотности электронов Γ_n ничем, вообще говоря, не выделены по сравнению с неполностью заполненными уровнями. На рис. 10.4 точками показаны расчетные значения, соответствующие заполнению 1, 2, 3-го и т. д. уровней Ландау.

Экспериментально зависимость R_xy = f (Γ_n) наблюдается легко при изменении Γ_n путем вариации напряжения на затворе V_G.

 

Рис. 10.4. Зависимость холловского сопротивления Rxy от избытка электронов Γn: а - в отсутствие магнитного поля; б - расчетная зависимость, точками обозначены состояния полного заполнения уровней Ландау; в - экспериментальная зависимость

 

Экспериментальное исследование на холловских МДП-транзисторах показало, что на месте полного заполнения уровней Ландау возникают ступеньки на зависимости холловского сопротивления R_xy от избытка электронов Γ_n. Величина холловского сопротивления на этих ступеньках R_xy определяется только универсальными физическими постоянными – постоянной Планка h и зарядом электрона q. Само значение R_xy при i = 1 равно:             

(10.10)

и в настоящее время служит в качестве эталона Ома.

Появление ступенек на зависимости холловского сопротивления R_xy от величины избытка электронов Γ_n или индукции магнитного поля B получило название квантового эффекта Холла. Автор открытия, западногерманский физик Клаус фон Клитцинг, удостоен Нобелевской премии 1985 года по физике.