Рентгеноструктурный анализ аморфных материалов
2.2. Скопление точечных атомов
Рассмотрим рассеяние рентгеновских лучей системой, состоящей из одинаковых, не взаимодействующих друг с другом математических точек, хаотически распределенных в объеме V (идеальный газ).
Среднее значение интенсивности рассеяния такой системой, исходя из формулы (2.1), с учетом, что fp=fq=f, запишем как
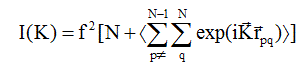 ( 2.2 )
( 2.2 )
Усреднение проводится по всем возможным мгновенным конфигурациям точек системы. Средние значения для всех слагаемых в двойной сумме будут одинаковы, и всего таких слагаемых будет N(N -I). Для одной, отдельно взятой, пары атомов р и q получим :
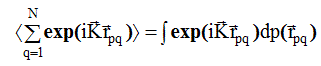 , где dp(rpq) дается формулой (1.1), и всего таких слагаемых будет N(N-I).
, где dp(rpq) дается формулой (1.1), и всего таких слагаемых будет N(N-I).
или,исходя из формулы (1.1),
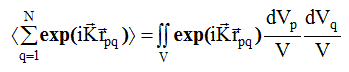 (2.3)
(2.3)
Поскольку взаимное расположение точек независимо, двойной интеграл в (2.3) можно рассматривать как произведение двух интегралов
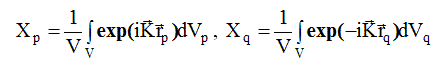 (2.4)
(2.4)
Будем считать объем V сферическим и выберем началом координат в центре сферы радиуса R (ри c .З). Элемент объема dV в сферических координатах записывается в виде:
dV=r2sinαdrddαdφ
Объем dV заключен между двумя сферами, радиусы которых r и r+dr, двумя конусами с углами раствора α и α+dα и двумя полуплоскостями, которые расположены под углами φ и φ+dφ(рис.3).
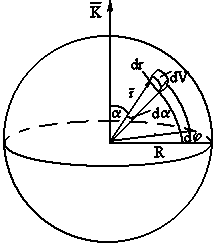
Рис.3. Сфера радиуса R, по объему которой проводится интегрирование в формуле (2.4)
Интеграл Xp запишется в виде:
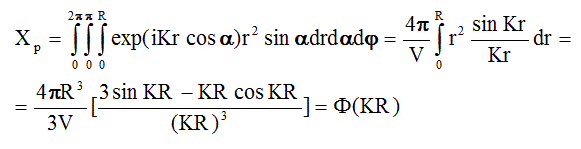
поскольку 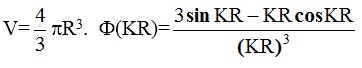 (2.7) - функция Релея.
(2.7) - функция Релея.
Она представляет собой амплитуду волны, рассеянной под углом 2 u к падающему лучу веществом, равномерно распределенным по объему сферы радиуса R.
Аналогично Sin(KR)/KR определяет амплитуду волны, рассеянной при тех же условиях веществом, равномерно распределенным по поверхности сферы радиуса R.
Основные свойства этих двух функций одинаковы; оба они равны единице при КR= 0 , спадают до нуля при КR =1,43 π для Ф(RK ) и КR= p для ![]() ,
затем осциллируют около оси абсцисс с затухающими с ростом К R амплитудами (рис.4а).
,
затем осциллируют около оси абсцисс с затухающими с ростом К R амплитудами (рис.4а).

Рис.4; а -Ход функций Ф(x)- кривая I и ![]() - кривая 2. б - Кривая распределения интенсивности рассеяния идеальным газом [I] .
- кривая 2. б - Кривая распределения интенсивности рассеяния идеальным газом [I] .
Так как Xq=Xp, то для интенсивности рассеяния, исходя из ( 2 .2) и (2 .7), получаем
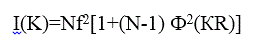 (2.8)
(2.8)
Значения функции Ф 2 (КR) при KR >1.43 π (рис.4) становятся настолько малы, что вторым слагаемым в ( 2 .8) можно пренебречь, и тогда
![]() (2.9)
(2.9)
Это соотношение имеет место практически при всех углах, при которых можно экспериментально ннаблюдать рассеяние, так как значение R обычно ~1 мм, λ~1 8A о и КR = 1,433 π уже при θ порядка сотых долей секунды.
Таким образом, в случае идеального газа средняя интенсивность рассеянного излучения будет равна сумме интенсивностей волн, рассеянных различными атомами. Это следствие того факта, что при хаотическом распределении рассеивателей разности фаз между волнами, рассеянными отдельными точками, меняются хаотически. При. К=0, θ =0 независимо от величины радиуса рассеивающего объема R и функции Ф(КR)=1. Отсюда
I(0)=N2f2, (2.10)
то есть в направлении первичного луча нет разности хода между волнами , рассеянными различными точками. Кривая распределения интенсивности рассеяния рассматриваемой системой частиц имеет вид, представленная на рис.46.
Узкий и острый максимум при К = 0 имеет место при рассеянии любой системой частиц. В кристалле он соответствует спектру нулевого порядка .
Форма этого максимума зависит от формы рассеивающего объекта; ширина определяется отношением (λ/R) , а также степенью немонохроматичности и не параллельности падающего пучка.