Рентгеноструктурный анализ аморфных материалов
2.3. Рассеяние скоплением одинаковых атомов конечного размера
При рассмотрении теории рассеяния скоплением одинаковых атомов конечного размера в условии предыдущей задачи следует лишь заменить точечные атомы на атомы, имеющие радиус R а. Взаимное расположение таких атомов будет характеризоваться сферически симметричной функцией W(r), то есть вероятность нахождения атомов р и q на расстоянии друг от друга будет задаваться формулой (1.3).
Тогда в выражении (2.3) - двойной интеграл, обозначим его Y запишем как
![]() (2.11)
(2.11)
Представим W (г) в виде 1 -[1- W( r)]. Тогда Y можно записать как сумму двух интегралов;
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
Интеграл Y1=XpXq = Ф2(KR) ( согласно проведенному в предыдущем разделе расчету).
Для оценки Y2 предположим, что атом р может находиться где угодно в объеме V, и свяжем с ним начало координат. Положение атома q будет зависеть от того, где находится атом р, тогда
![]()
или, подставив dVp в сферических координатах (2.5) и проинтегрировав по φ получим
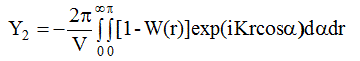 (2.14)
(2.14)
Бесконечный предел при интегрировании по r обоснован тем, что при больших r ![]() , то есть 1 – W(r ) обращается в 0. Окончательно имеем
, то есть 1 – W(r ) обращается в 0. Окончательно имеем
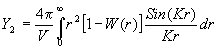 (2.15)
(2.15)
Откуда
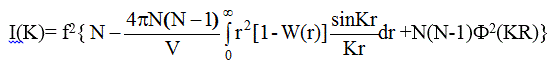 (2.16)
(2.16)
Последнее слагаемое обозначим Im(K)
![]() (2.17)
(2.17)
Как следует из анализа формулы (2. 8), Im(K) имеет заметные значения только в непосредственной близости к первичному пучку,. Такое рассеяние называют малоугловым и при анализе результатов исследования им обычно пренебрегают.
Формула (2.16) описывает рассеяние любым изотропным скоплением, состоящим из одинаковых атомов конечного размера.
Если порядок в расположении атомов в исследуемом материале характеризуется функцией W(r), представленной на рисунке 2а , то есть аналогичен порядку, имеющему место в разреженном газе, то, так как
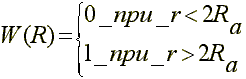
интегрирование в (2.16) можно ограничить пределом, равным 2 Ra . Функция I (К) без учета Im (К) имеет вид :
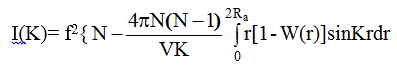 (2.18)
(2.18)
Проведя интегрирование, получим
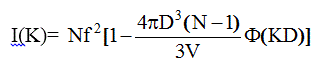 , где D=2Ra (2.19)
, где D=2Ra (2.19)
Заменим N -I на N , поскольку N>> 1 , и обозначим ![]() через W
- объем сферы действия всех молекул в объеме V, тогда
через W
- объем сферы действия всех молекул в объеме V, тогда
![]() (2.20)
(2.20)
Формула (2.20) впервые выведена Дебаем. Если газ находится при нормальном давлении, то Ω/V настолько мало, что вторым слагаемым в (2.20) можно пренебречь. Тогда I(K)=Nf2 , то есть такой газ рассеивает как идеальный.
С увеличением давления вклад второго слагаемого становятся заметный. Рис.5 иллюстрирует изменение вида кривой I (К) при возрастании Ω/V.
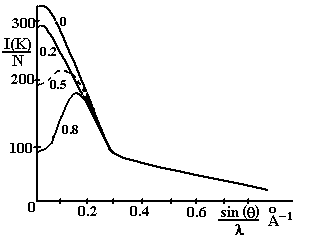
Рис.5. Графики функции I(K)/N для аргона Аr [ 1]. Цифру при кривых указывают значения Ω/V. D=4 Ао
Нужно, однако, отметить, что кривые, приведенные на рис.5, характеризуют процесс изменения картины рассеяния чисто качественно, поскольку вид функции W(r ) в газах, находящихся при высоких давлениях, изменяется (рис.2б). Тем не менее четко прослеживается важная общая закономерность : при нормальных давлениях рассеяние в газе стремится к максимуму при малых углах; сжатие газа приводят к уменьшению рассеяния при малых углах и появлению отчетливого максимума -дифракционного гало, угловое положение которого зависят от D . Максимальное сжатие приводит к снижениюю газа, следовательно, появление гало должно иметь место и в жидком состоянии. С другой сторону, аморфное твердое тело можно рассматривать как замороженную жидкость, то есть материал, в котором практически отсутствует диффузионное перемещение частиц. Последнее приводит и тому, что на дифракционной картине, при сохранении общего ее характера, наблюдается только сужение пиков, то есть гало становится менее диффузным. Это подтверждает, что нет резкого различия между теорией дифракция в газах, жидкостях и аморфных твердых телах: различие определяется видом функции W(r ) (рис.2).
Цернике и Принс показали, что исходя из (2.16) можно найти W(r), p (r ) или p e(r ) экспериментально. Обозначим любое (атомное или электронное) распределение плотности через p( r ) , а соответствующее среднее значение - через ro.
Заменяя в (2.16) W (г) на p( r ) и опуская Im(K) , перепишем (2.16) в виде:
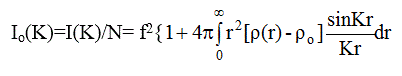 (2.21)
(2.21)
Вводя интерференционную функцию распределения интенсивности рассеяния, как
![]() (2.22)
(2.22)
получим для K-взвешенной интерференционной функции выражение:
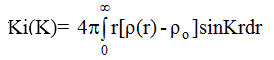 (2.23)
(2.23)
Обозначив h(K) = Ki(K), а 4πr[p(r)-po] = g(r), запишем
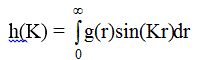 (2.24)
(2.24)
Функция h(K) является Фурье-трансформантой функции g(r), следовательно,
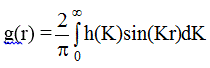 (2.25)
(2.25)
или
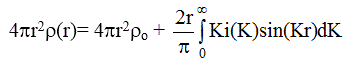 (2.26)
(2.26)
Таким образом, кривая распределения интенсивности рассеяния, определенная в обратном пространстве, связана Фурье - преобразованием с распределением атомной или электронной плотности в пространстве объекта. Определяя i(K ) из эксперимента, численным интегрированием рассчитывают кривую D(R) = 4πr2p(r).