|
В вопросах
организации обработки информации с помощью ЭВМ важное место занимают
системы счисления, формы представления данных и специальное кодирование
чисел.
1. Системы счисления
Совокупность
приемов наименования и записи чисел называется счислением. Под
системой счисления понимается способ представления любого числа с
помощью ограниченного алфавита символов, называемых цифрами. Счисление
представляет собой частный случай кодирования, где слово, записанное с
использованием определенного алфавита и по определенным правилам,
называется кодом. Применительно к счислению это код числа.
Позиционные и непозиционные системы счисления.
Различают позиционные и непозиционные системы счисления. В непозиционных
системах счисления каждое число обозначается соответствующей совокупностью
символов. Характерным представителем непозиционных систем является римская
система счисления со сложным способом записи чисел и громоздкими правилами
выполнения арифметических операций. Например, запись MCMXCIX означает, что
записано число 1999 (М — тысяча, С — сто, Х — десять, V — пять, I —
единица и т. д.).
Позиционные системы счисления обладают большими преимуществами в
наглядности представления чисел и в простоте выполнения арифметических
операций.
В позиционной системе счисления значение числа определяется не только
набором входящих в него цифр, но и их местом (позицией) в
последовательности цифр, изображающих это число, например, числа 127 и
721.
Позиционной является десятичная система счисления, используемая в
повседневной жизни. Помимо десятичной существуют другие позиционные
системы счисления, и некоторые из них нашли применение в информатике.
Количество символов, используемых в позиционной системе счисления,
называется ее основанием. Его обозначают обычно буквой q. В десятичной
системе счисления используется десять символов (цифр): 0, 1, 2, 3,4, 5, 6,
7, 8, 9, и основанием системы является число десять.
Особое место среди позиционных систем счисления занимают системы со
степенными весами разрядов, в которых веса смежных позиций цифр (разрядов)
отличаются по величине в постоянное количество раз, равное основанию q
системы счисления.
В общем случае в такой позиционной системе счисления с основанием q любое
число Х может быть представлено в виде полинома разложения:
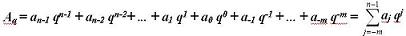 (1.1)
(1.1)
где:
A(q) — запись числа в системе счисления с основанием q;
q — основание системы счисления;
ai — целые числа, меньше q;
п — число разрядов (позиций) в целой части числа;
т — число разрядов в дробной части числа.
Например:
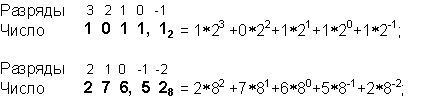
Для обозначения используемой системы счисления ее основание указывается в
индексе. Изображение числа A в виде последовательности коэффициентов a.
полинома является его условной сокращенной записью (кодом).
A(q)=an-1 an-2…a1a0,a-1…a-m (1.2)
Запятая отделяет целую часть числа от дробной и служит началом отсчета
значений веса каждой позиции (разряда).
В информатике применяют позиционные системы счисления с недесятичным
основанием: двоичную, восьмеричную и шестнадцатеричную, т. е. системы
счисления с основанием q = 2k , где k=1,3,4.
Двоичная система счисления
Наибольшее распространение получила двоичная система счисления, В этой
системе для представления любого числа используются два символа — цифры 0
и 1. Основание системы счисления q = 2.
Произвольное число с помощью формулы (1.1) можно представить в виде
разложения по степеням двойки. Тогда условная сокращенная запись в
соответствии с (1.2) означает изображение числа в двоичной системе
счисления (двоичный код числа), где ai =0 или 1.
Например:
15,625=1•23+1•22+1•21+1•20+ 1•2-1+0•2-2+1•2-3= 1111,101(2)
Двоичное представление числа требует примерно в 3,3 раза большего числа
разрядов, чем его десятичное представление. Тем не менее, применение
двоичной системы счисления создает большие удобства для работы ЭВМ, т. к.
для представления в машинеразряда двоичного числа может быть использован
любой запоминающий элемент, имеющий два устойчивых состояния.
Восьмеричная система счисления.
В восьмеричной системе счисления алфавит состоит из восьми символов (цифр):
0, 1 ... 7. Основание системы счисления q = 8. Для записи произвольного
числа в восьмеричной системе счисления необходимо по формуле (1.1) найти
его разложение по степеням восьмерки, а затем воспользоваться условной
сокращенной записью (1.2).
Например, десятичное число 53(10) = 65(8)
Шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления алфавит включает в себя 16 символов
(цифр и букв) : 0, 1 ... 9, А, В, С, D, Е, F. Основание системы счисления
q = 16. Для записи произвольного числа в этой системе счисления необходимо
по формуле (1.1) найти его разложение по степеням 16, а по формуле (1.2) —
код.
Например: 31(10)=1F(16)
Двоично-десятичное кодирование.
Наряду с двоичными кодами, которыми оперирует ЭВМ, для ввода и вывода
десятичных чисел (данных) используют специальное двоично-десятичное
кодирование. При двоично-десятичном кодировании каждая десятичная цифра
заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются
последовательно в соответствии с порядком следования десятичных цифр. При
обратном преобразовании двоично-десятичного кода в десятичный исходный код
разбивается на тетрады вправо и влево от запятой, которые затем заменяются
десятичными цифрами.
Таким образом, при двоично-десятичном кодировании фактически не
производится перевод числа в новую систему счисления, а мы имеем дело с
двоично-кодированной десятичной системой счисления.
Например, десятичное число 12(10) = C(16)= 14(8)= 1100(2)= 00010010(2-10).

2. Преобразование чисел
ЭВМ работают
с двоичными кодами, пользователю удобнее иметь дело с десятичными или
шестнадцатеричными. Поэтому возникает необходимость перевода числа из
одной системы счисления в другую.
Преобразование числа Х из системы счисления с основанием q в систему
счисления с основанием р осуществляется по правилу замещения или по
правилу деления-умножения на основание системы счисления.
Правило замещения
Правило замещения реализуется на основании формулы (1.1) и предусматривает
выполнение арифметических операций с кодами чисел в новой системе
счисления. Поэтому оно чаще всего используется для преобразования чисел из
недесятичной системы счисления в десятичную.
Пример.111011,011(2)= 1•24 +0•23 +1•22 +0•21
+l•20+0•2-1+l•2-2+l•2-3= 59, 375.
Правило деления-умножения
Правило деления-умножения предусматривает выполнение арифметических
операций с кодами чисел в исходной системе счисления с основанием q,
поэтому его удобно применять для преобразования десятичных чисел в любые
другие позиционные системы счисления. Правила преобразования целых чисел и
правильных дробей различны. Для преобразования целых чисел используется
правило деления, а для преобразования правильных дробей — правило
умножения. Для преобразования смешанных чисел используются оба правила
соответственно для целой и дробной частей числа.
Правило деления используется для преобразования целого числа, записанного
в q-ичной системе счисления, в р-ичную. В этом случае необходимо
последовательно делить исходное q-ичное число и получаемые частные на
новое основание р, представленное в q-ичной системе счисления. Деление
продолжают до тех пор, пока очередное частное не станет меньше р. После
замены полученных остатков и последнего частного цифрами р-ичной системы
счисления записывается код числа в повои системе счисления. При этом
старшей цифрой является последнее частное, а следующие за ней цифры
соответствуют остаткам, записанным в последовательности, обратной их
получению.
Правило умножения используется для преобразования дробного числа,
записанного в q-нчнон системе счисления, в р-ичпую. В этом случае
необходимо последовательно умножать исходную дробь и дробные части
получающихся произведений на основание р, представленное в исходной q-ичной
системе счисления. Целые числа получаемых произведений, замененные цифрами
р-ичной системы счисления, и дают последовательность цифр в новой р-ичной
системе.
Умножение необходимо производить до получения в искомом р-ичном коде цифры
того разряда, вес которого меньше веса младшего разряда исходной q-ичной
дроби. При этом в общем случае получается код приближенно, и всегда с
недостатком значения дроби. Поэтому в случае обратного преобразования (р-ичпого
кода дроби в q-ичный) результат может не совпадать с исходным значением q-ичной
дроби.
Пример.75,35(10)=1001011,01011…(2) .
Для получения частных и остатков по правилу деления для целой части числа
удобно использовать формулу записи, известную под названием «деление в
столбик», а для получения р-ичного кода дробной части числа по правилу
умножения — форму записи, известную под названием «умножение столбиком».
Применительно к рассматриваемому примеру имеем:
Таким образом, в результате преобразования получаем 75,35(10) =
1001011,01011...(2). Как следует из примера, процесс перевода дробной
части можно продолжить до бесконечности. ЭВМ оперирует числами,
представленными конечными наборами цифр. Поэтому дроби округляют в
соответствии с правилами преобразования и весом младшего разряда исходной
дроби.
Преобразование чисел из двоичной системы счисления в восьмеричную,
шестнадцатеричную и обратно осуществляется по упрощенным правилам с учетом
того, что основания этих систем счисления кратны целой степени 2, т. е.
8=23 , а 16=24 . Это означает, что при преобразовании восьмеричного кода
числа в двоичный, необходимо каждую восьмеричную цифру заменить
соответствующим трехзначным двоичным кодом (триадой).
При преобразовании шестнадцатеричного кода числа в двоичный необходимо
каждую шестнадцатеричную цифру заменить четырехзначным двоичным кодом (тетрадой).
При преобразовании двоичного кода в восьмеричный или шестнадцатеричный
двоичный код делится соответственно на триады или тетрады влево и вправо
от запятой (точки), разделяющей целую и дробные части числа. Затем триады
(тетрады) заменяются восьмеричными (шестнадцатеричными) цифрами.
Например:

Если при разбиении двоичного кода в крайних триадах (тетрадах) недостает
цифр до нужного количества, они дополняются нулями. Соответственно, «лишние»
нули слева и справа, не вошедшие в триады (тетрады) отбрасываются.

3.
Формы представления данных
В ЭВМ используются следующие формы представления данных:
• числа с фиксированной точкой (запятой);
• числа с плавающей точкой (запятой);
• десятичные числа;
• символьные данные.
Числа с фиксированной точкой
При представлении числа Х в форме с фиксированной точкой указываются знак
числа (sign X) и модуль числа (modX) в q-ичном коде. Иногда такую форму
представления чисел называют естественной формой. Место точки (запятой)
постоянно для всех чисел и в процессе решения задач не меняется. Знак
положительного числа кодируется цифрой «0», а знак отрицательного числа —
цифрой «1».
Код числа в форме с фиксированной точкой, состоящий из кода знака и q-ичного
кода его модуля, называется прямым кодом. Разряд прямого кода числа, в
котором располагается код знака, называется знаковым разрядом кода.
Разряды прямого кода числа, в которых располагается q-ичный код модуля
числа, называются цифровыми разрядами кода. При записи прямого кода
знаковый разряд располагается левее старшего цифрового разряда и обычно
отделяется от цифровых разрядов точкой.
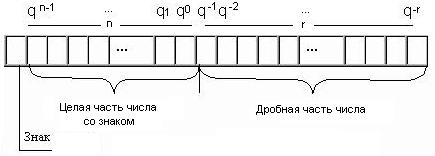
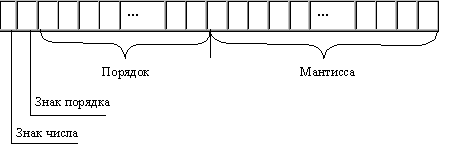
В общем случае разрядная сетка ЭВМ для размещения чисел в форме с
фиксированной точкой показана на рисунке.
На рисунке показано п разрядов для представления целой части числа и
r разрядов — для дробной части числа.
a) фиксированная
При заданных п иr диапазон изменения модулей чисел, коды которых могут
быть представлены в данной разрядной сетке, определяется неравенством
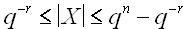
Использование формы с фиксированной точкой для представления смешанных (с
целой и дробной частью) чисел в ЭВМ практически не встречается. Как
правило, используются ЭВМ либо с дробной арифметикой (п=0), либо с
целочисленной арифметикой (r=0).
Форма представления чисел с фиксированной точкой упрощает аппаратную
реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при
решении задач на машине необходимо постоянно следить за тем, чтобы все
исходные данные, промежуточные и окончательные результаты находились в
допустимом диапазоне представления. Если этого не соблюдать, то возможно
переполнение разрядной сетки, и результат вычислений будет неверным. От
этих недостатков в значительной степени свободны ЭВМ, использующие форму
представления чисел с плавающей точкой, или нормальную форму.
Числа с плавающей точкой
b) рис 14.б с плавающей точкой
В нормальной форме число представляется в виде произведения X=mqp
где т — мантисса числа;
q — основание системы счисления;
р — порядок.
Для задания числа в нормальной форме требуется задать знаки мантиссы и
порядка, их модули в q-ичном коде, а также основание системы счисления.
Нормальная форма представления чисел неоднозначна, ибо взаимное изменение
т и р приводит к плаванию точки (запятой). Отсюда произошло название формы
представления чисел.
Для однозначности представления чисел в ЭВМ используется нормальная
нормализованная форма, в которой положение точки всегда задается перед
значащей цифрой мантиссы, т. е. выполняется условие
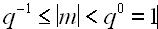
В общем случае разрядную сетку ЭВМ для размещения чисел в нормальной форме
можно представить в виде, изображенном на рис. Разрядная сетка содержит:
-
разряд для знака мантиссы;
-
r цифровых разрядов для q-ичного кода модуля мантиссы;
-
разряд для кода знака порядка;
-
s разрядов для q-ичного кода модуля порядка.
Диапазон представления модулей чисел в нормальной нормализованной форме
определяется следующим неравенством:
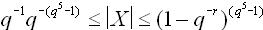
В конкретной ЭВМ диапазон представления чисел с плавающей точкой зависит
от основания системы и числа разрядов для представления порядка.
При этом у одинаковых по длине форматов чисел с плавающей точкой с
увеличением основания системы счисления существенно расширяется диапазон
представляемых чисел.
Точность вычислений при использовании формата с плавающей точкой
определяется числом разрядов мантиссы r. Она увеличивается с увеличением
числа разрядов.
При представлении информации в виде десятичных многоразрядных чисел каждая
десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена
информацией, экономии памяти и удобства операций над десятичными числами
предусматриваются специальные форматы их представления: зонный (распакованный)
и упакованный. Зонный формат используется в операциях
ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и
распаковки десятичных чисел.

4.
Понятие о специальном кодировании чисел
Для хранения чисел и выполнения различных операций над ними их
представляют различными кодами: прямым, обратным и дополнительным. Как уже
отмечалось выше, для представления чисел со знаками в памяти ЭВМ
используют прямой код. Для обозначения прямого кода числа Х используется
запись вида [X ]^ .
Правило представления Q-ичного кода числа в прямом коде
имеет вид:
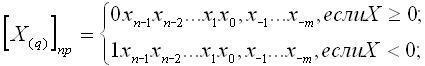
где хi— значение цифры в i-м разряде исходного кода.
Здесь старший бит несет информацию о знаке числа. Если он принимает
значение 0, то знак числа «+» ; если значение 1 — то знак числа «-».
Например, для двоичного кода
| Х(2)= +11001011 |
[Х(2)]=0.11001011; |
| Х(2)= -01101011 |
[Х(2)]=1.01101011. |
При представлении чисел в прямом коде реализация арифметических операций в
ЭВМ должна предусматривать различные действия с модулями чисел в
зависимости от их знаков. Так, сложение в прямом коде чисел с одинаковыми
знаками выполняется достаточно просто. Числа складываются и сумме
присваивается код знака слагаемых. Значительно более сложной является
операция алгебраического сложения в прямом коде чисел с различными знаками.
В этом случае приходится определять большее по модулю число, производить
вычитание чисел и присваивать разности знак большего по модулю числа. Для
упрощения выполнения операций алгебраического сложения в ЭВМ используются
специальные коды, позволяющие свести эту операцию к операции
арифметического сложения. В качестве специальных в ЭВМ применяются
обратный и дополнительный коды. Они образуются из прямых кодов чисел,
причем специальный код положительного числа равен его прямому коду.
Для обозначения обратного кода числа Х(q) используется запись вида [Х(q)]обр.
Правило представления q-ичного кода числа в обратном коде
имеет вид:
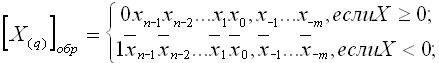
Здесь инверсия цифры хi , определяемая из соотношения:
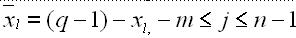
где: q — основание системы счисления;
xj значение цифры в i-ом разряде исходного кода.
Для двоичной системы счисления, если х = 1, то
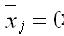 и наоборот. Отсюда можно
сформулировать частное правило образования обратного кода для
отрицательных двоичных чисел. и наоборот. Отсюда можно
сформулировать частное правило образования обратного кода для
отрицательных двоичных чисел.
Для преобразования прямого кода двоичного отрицательного числа в обратный
код и наоборот необходимо знаковый разряд оставить без изменения, а в
остальных разрядах нули заменить на единицы, а единицы на нули.
Например:
| x(2)= +11011001, |
[X(2)] пр.=0.11011001, |
[X(2)] обр.=
0.11011001. |
| x(2)= - 01011101, |
[X(2)] пр.=1.01011101, |
[X(2)] обр.=
1.10100010. |
Для обозначения дополнительного кода числа Х(q) используется
запись вида [X(q)]доп . Правило представления q-ичного кода
числа в дополнительном коде имеет вид:
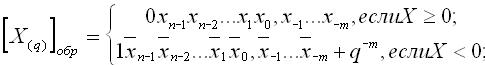
Таким образом, для преобразования прямого кода q-ичного
отрицательного числа в дополнительный необходимо образовать его в обратный
код и в младший разряд добавить единицу.
Например, для двоичных чисел:
| x(2)= +11011001, |
[X(2)] пр.= 0.11011001, |
[X(2)]доп.= 0.11011001. |
| x(2)= - 01011101, |
[X(2)] пр.=1.01011101, |
[X(2)]обр.= 1.10100011. |
При выполнении операции сложения чисел, представленных специальными q-ичными
кодами знаковые разряды участвуют в операции наряду с цифровыми разрядами.
При этом цифровые разряды слагаемых складываются как модули чисел по
правилам q-ичной арифметики. Знаковые разряды и цифры переноса из старшего
цифрового разряда при любом основании системы счисления (q=2)
складываются как одноразрядные двоичные коды. Если при этом формируется
перенос из знакового разряда, то он имеет вес единицы младшего разряда q-m
при использовании обратного кода и должен быть добавлен в младший разряд
результата. При использовании дополнительного кода единица переноса из
знакового разряда не принимается во внимание, т. е. отбрасывается.
Например:


При выполнении операции алгебраического сложения перед преобразованием
прямых кодов слагаемых в специальные необходимо их выровнять по числу
разрядов, если число разрядов слагаемых различно. Кроме того, в некоторых
случаях может произойти переполнение разрядов сетки. Признаком
переполнения разрядной сетки является следующая комбинация цифр в знаковых
разрядах слагаемых и результата:
0+0 = 1
или
1+1 = 0
Результат сложения специальных кодов чисел при переполнении разрядной
сетки является неверным.

|