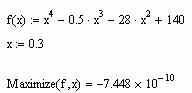Поиск экстремума функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. С помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется сначала вычислить все их локальные значения и потом выбрать наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
где:
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения.
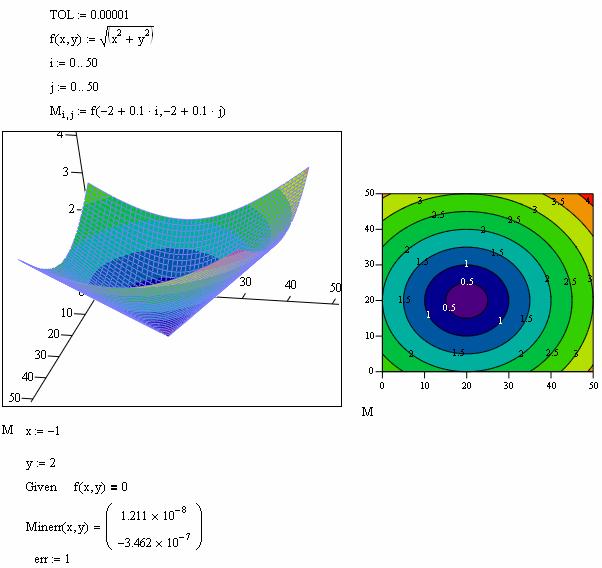
Поиск экстремума функции нескольких переменных. Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной. Но также поиск экстремума можно организовать с помощью функции Minerr:
Примеры: |