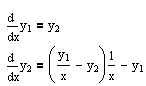Дифференциальные уравнения и системы уравнений
В Mathcad имеются три встроенные функции, которые позволяют решать задачу Коши различными численными методами.
где: y0 - вектор начальных значений в точке t0 размера n*1; t0 -начальная точка расчета; t1 -конечная точка расчета; M - число шагов, на которых численный метод находит решение; D - векторная функция размера n*1 двух аргументов — скалярного t и векторного у. При этом у — искомая векторная функция аргумента t того же размера n*1.
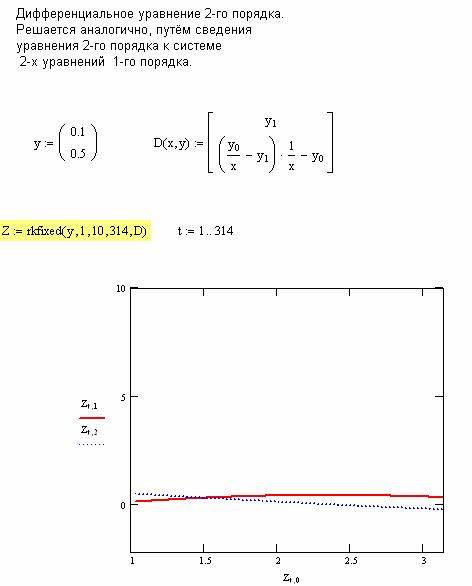
Дифференциальные уравнения 2-го порядка. Решаются аналогично, путём сведения уравнения 2-го порядка к системе 2-х уравнений 1-го порядка. Дано:
y1(0) = 0.1; y2(0) = 0.5 Решение на Mathcad:
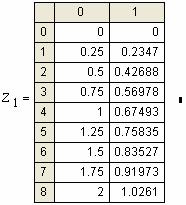
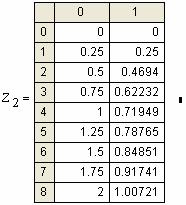
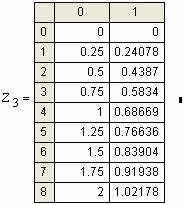
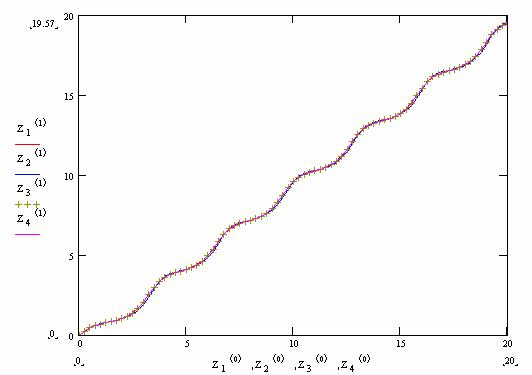
Примеры: |