11. Численное решение систем нелинейных уравнений
Постановка задачи.
Требуется решить систему нелинейных уравнений 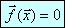 (1). В координатном виде эту задачу можно записать так:
(1). В координатном виде эту задачу можно записать так: 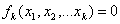 , где 1 ≤ k ≤ n.
, где 1 ≤ k ≤ n.
Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.
Метод Ньютона.
Обозначим 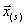 некоторое приближение к корню системы уравнений
некоторое приближение к корню системы уравнений 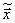 . Пусть малое
. Пусть малое 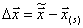 . Вблизи
. Вблизи 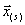 каждое уравнение системы можно линеаризовать следующим образом:
каждое уравнение системы можно линеаризовать следующим образом:
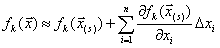 , 1 ≤ k ≤ n. (2)
, 1 ≤ k ≤ n. (2)
Это можно интерпретировать как первые два члена разложения функции в ряд Тейлора вблизи 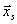 . В соответствии с (1), приравнивая (2) к нулю, получим:
. В соответствии с (1), приравнивая (2) к нулю, получим:
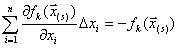 , 1 ≤ k ≤ n. (3)
, 1 ≤ k ≤ n. (3)
Мы получили систему линейных уравнений, неизвестными в которой выступают величины 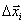 . Решив ее, например, методом Гаусса, мы получим некое новое приближение к
. Решив ее, например, методом Гаусса, мы получим некое новое приближение к 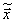 , т.е.
, т.е. 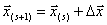 . Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе:
. Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе:
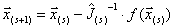 , (4)
, (4)
где в данном случае
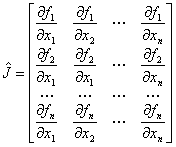 – матрица Якоби, которая считается для каждого (s) приближения.
– матрица Якоби, которая считается для каждого (s) приближения.
Критерием окончания итерационного процесса является условие 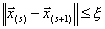 (Можем принять под
(Можем принять под 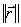 как норму
как норму 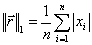 , так и
, так и 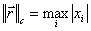 ). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если
). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если 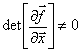 , то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.
, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.
Блок-схема метода Ньютона для решения систем нелинейных уравнений.
Так как метод Ньютона отличается высокой скоростью сходимости при выполнении условий сходимости, на практике критерием работоспособности метода является число итераций: если оно оказывается большим (для большинства задач >100), то начальное приближение выбрано плохо.
Частным случаем решения (4) методом Ньютона системы из двух нелинейных уравнений
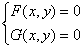
являются следующие легко программируемые формулы итерационного процесса:
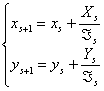 , где
, где 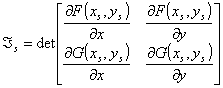 ,
,
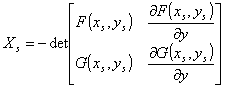 ,
, 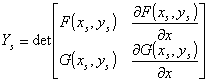
Метод простых итераций.
Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение 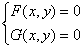 , а исходная система уравнений преобразуется к эквивалентной системе вида
, а исходная система уравнений преобразуется к эквивалентной системе вида
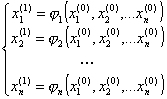 , (5)
, (5)
и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим 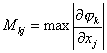 . Достаточным условием сходимости является
. Достаточным условием сходимости является 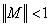 . Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций
. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций 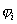 , которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
Например, для исходной системы уравнений 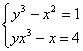 эквивалентная итерационная система (5) может быть представлена в следующем виде:
эквивалентная итерационная система (5) может быть представлена в следующем виде:
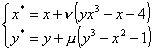 ,
,
где множители 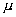 = –0.15 и
= –0.15 и 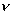 = –0.1 подбираются из анализа условий сходимости.
= –0.1 подбираются из анализа условий сходимости.
Метод спуска.
Рассмотрим функцию 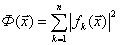 . Она неотрицательна и обращается в нуль в том и только в том случае, если
. Она неотрицательна и обращается в нуль в том и только в том случае, если 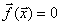 . То есть, если мы найдем глобальный минимум
. То есть, если мы найдем глобальный минимум 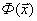 , то полученные значения
, то полученные значения 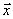 как раз и будут решениями уравнения (1). Подробнее о решении таких задач см. следующую главу.
как раз и будут решениями уравнения (1). Подробнее о решении таких задач см. следующую главу.
<<Назад
Далее >>
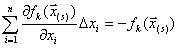 , 1 ≤ k ≤ n. (3)
, 1 ≤ k ≤ n. (3) – матрица Якоби, которая считается для каждого (s) приближения.
– матрица Якоби, которая считается для каждого (s) приближения.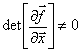 , то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.
, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами. 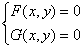
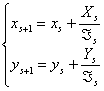 , где
, где 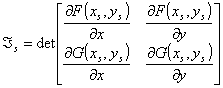 ,
, 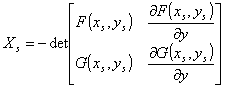 ,
, 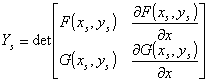
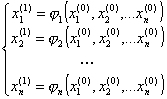 , (5)
, (5)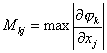 . Достаточным условием сходимости является
. Достаточным условием сходимости является 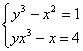 эквивалентная итерационная система (5) может быть представлена в следующем виде:
эквивалентная итерационная система (5) может быть представлена в следующем виде: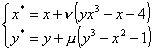 ,
,