7.4.1. Молекулярное поле Вейсса

Для объяснения появления спонтанного магнитного момента быстро вращающегося железного стержня и спонтанного магнитного момента Вейсс высказал предположение о существовании в ферромагнетиках внутреннего молекулярного поля . Согласно Вейссу внутреннее магнитное поле подобно внешнему магнитному полю  в парамагнетиках и создает в кристалле ферромагнетика параллельную ориентацию магнитных моментов атомов в отсутствие внешнего магнитного поля (B = 0). Предполагалось, что поле  пропорционально намагниченности по закону

,

(7.31)

где  − постоянная молекулярного поля. Тогда эффективное поле , действующее на атом в ферромагнетике, должно складываться из внешнего магнитного поля  и молекулярного поля :

.

(7.32)

Используя выражения для намагниченности (7.24) и эффективного поля (7.32), получим для намагниченности ферромагнетика в случае слабых полей и не очень низких температур

.

(7.33)

Вводя, как мы это делали при выводе формулы (7.25), постоянную Кюри  и температуру Кюри  (точка Кюри), получим выражение для магнитной восприимчивости атома ферромагнетика

.

(7.34)

Выражение (7.34) получило название закона Кюри–Вейсса, и оно очень хорошо описывает наблюдаемые изменения магнитной восприимчивости в парамагнитной области (выше температуры Кюри). Закон Кюри–Вейсса можно рассматривать как закон Кюри с началом отсчета температуры в точке Кюри. По формуле Ланжевена (7.23) полное упорядочение магнитных моментов в парамагнетике под действием внешнего поля наступает только при абсолютном нуле температуры. У ферромагнетика такое упорядочение имеет место уже при температуре Кюри .

Результирующий магнитный момент единицы объема ферромагнетика, содержащего N атомов, т. е. намагниченность, при температуре, стремящейся к нулю, стремится к значению

,

(7.35)

где g – фактор расщепления Ланде (или g-фактор). Физический смысл g-фактора  рассматривается в квантовой теории парамагнетизма. Заметим лишь, что возникновение фактора Ланде связано с тем, что в магнитном поле энергетические уровни электронов расщепляются. Величина расщепления зависит от того, преобладает ли магнетизм, обязанный своим возникновением спиновым моментам электронов, либо главенствует магнетизм за счет орбитального момента. Для чисто спинового магнетизма g = 2, а для чисто орбитального g=1.

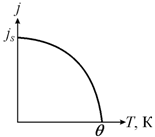
Выражение (7.32) показывает, что при низких температурах все спины ориентируются параллельно друг другу, т. е. имеет место ферромагнитное упорядочение в отсутствии внешнего поля. С повышением температуры самопроизвольная намагниченность ферромагнетика уменьшается и исчезает при температуре Кюри данного вещества. Схематично такая зависимость представлена на рис. 7.12. Видно, что уменьшение намагниченности происходит особенно резко в окрестности точки Кюри, но это уменьшение также заметно и при гораздо более низких температурах.

Спонтанная намагниченность ферромагнетиков обусловлена, как будет показано в следующем параграфе, взаимодействием между соседними атомами, которое стремится упорядочить их спины. Если это взаимодействие настолько сильно, что все соседние спины устанавливаются параллельно друг другу, намагниченность материала достигает своего максимального значения, т. е. возникает дальний магнитный порядок. Возникновение дальнего магнитного порядка является результатом как сильного взаимодействия ближайших соседних атомов, так и непрерывности кристалла. Однако тепловые колебания атомов стремятся нарушить спиновое упорядочение. Следовательно, максимальная намагниченность, характеризующаяся полным упорядочением всех спинов, должна наблюдаться лишь при наинизшей возможной температуре, т. е. при абсолютном нуле. В действительности такое упорядочение может не достигаться даже при абсолютном нуле из-за размагничивающего влияния таких факторов, как анизотропия, взаимодействие d-электронов с электронами проводимости, влияние дефектов решетки и др.

 

Рис. 7.12. Характер зависимости самопроизвольной намагниченности ферромагнетика от температуры

 

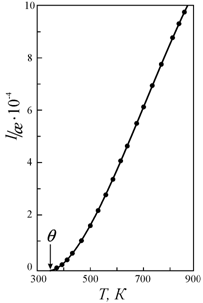
Большинство ферромагнетиков имеет достаточно большую магнитную восприимчивость и выше температуры Кюри q, и для них имеет место отклонение от закона Кюри–Вейсса. Наиболее близко соответствует этому закону поведение магнитной восприимчивости с ростом температуры у никеля, однако при температурах немного выше точки Кюри и его магнитная восприимчивость отклоняется от соответствия закону Кюри-Вейсса (рис. 7.13).

 

Рис. 7.13. Зависимость магнитной восприимчивости никеля от температуры [63]

 

Объяснение этого факта заключается в том, что, хотя тепловое движение атомов и разрушает дальний порядок в расположении спиновых магнитных моментов, некоторый спиновый порядок, хотя и более слабый, все же продолжает существовать. Он представляет собой своего рода ближний порядок в расположении спинов, когда данный атом окружен небольшой областью, в которой спины более или менее одинаково ориентированы. Это явление существует, по-видимому, во всех ферромагнитных твердых телах при температуре выше точки Кюри.

В табл. 7.1 [52] приведены значения самопроизвольной намагниченности, средние значения атомного магнитного момента , выраженные в магнетонах Бора (эффективное число магнетонов Бора), и температура Кюри некоторых ферромагнитных металлов и соединений.

 

Таблица 7.1

Значения намагниченности насыщения, эффективное число магнетонов Бора,

приходящихся на атом магнетика, и температура Кюри

Магнетик	Намагниченность насыщения, Вб/м2		(при 0 К)	, К
	при комнатной температуре	при температуре 0 К
Fe	1707	1752	2,221	1043
Co	1400	1446	1,716	1400
Ni	485	510	0,606	631
Gd	1090	1980	7,10	289
Dy	1830 (80 K)	−	−	105
MnBi	600	675	3,52	630
Cu2MnAl	430	580	4,0	603
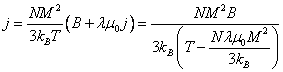