5.6.1. Фононные спектры в кристаллах

Энергетические спектры фононов в реальных веществах, как правило, очень сложны и для их описания необходимо знать детальный вид поверхностей постоянной частоты  в зоне Бриллюэна для всех ветвей спектра. Поверхности постоянной частоты определяют очень важную характеристику фононного спектра − функцию  спектральной плотности фононов, которая задает число волн, или мод, приходящееся на интервал частот от w до w+dw. Если обозначить количество волн в спектральном интервале  через dn, то спектральная плотность колебаний одномерной моноатомной цепочки определяется формулой

,

(5.63)

где N − число колеблющихся атомов, − максимальная частота колебаний в спектральном интервале. При низких частотах  пропорциональна , а вблизи  функция  D(w) имеет особенность корневого типа.

При наличии нескольких ветвей дисперсионных кривых, как это имеет место для реального кристалла, где число базисных атомов равно r и общее число ветвей колебаний 3r, плотность состояний определяется суммой

.

(5.64)

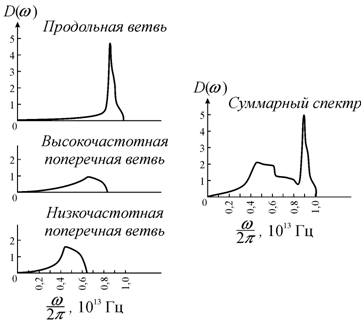
На рис. 5.13 показаны кривые спектральной плотности фононов для продольной и поперечных ветвей и суммарный спектр для алюминия. Значения частот, при которых кривые  имеют резкие перегибы и острые пики, называются критическими точками или сингулярностями Ван Хова. Этим значениям частот w соответствуют нулевые групповые скорости волн в некоторых направлениях. Параболический характер фононного спектра при малых частотах аналогичен спектру колебаний атомов одноатомной одномерной цепочки при малых частотах. Плотность состояний в этом случае имеет вид

.

(5.65)

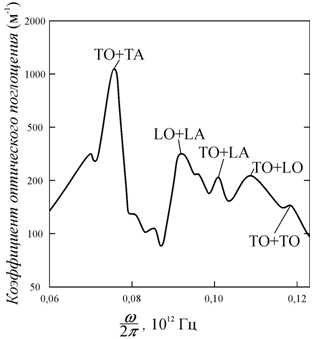
Резкий максимум на суммарной зависимости D(w) может быть связан с максимальной частотой некоторых типов фононов. В кристаллах со сложной многоатомной решеткой подобные особенности спектра могут быть связаны и с оптическими ветвями колебаний. На рис. 5.14 изображен фононный спектр кристалла кремния, где функцией является коэффициент оптического поглощения.

Резкие максимумы на представленной кривой связаны с возбуждением различных мод колебаний атомов кристалла кремния.

Рис. 5.13. Спектр колебаний в решетке алюминия [59]

Рис. 5.14. Вид фононного спектра в кристалле кремния (Si) [88]

 

Знание фононных спектров необходимо для анализа и расчета многих физических свойств твердых тел − оптических, тепловых, электрических и т. д. В экспериментах определяют дисперсионные кривые продольных и поперечных волн в направлениях высокой симметрии. Затем эта информация используется для численного расчета плотности состояний . При интерпретации спектров колебаний очень важным этапом является анализ критических точек.
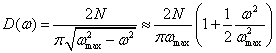