Глава 4
МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ

Современная наука и техника постоянно предъявляют высокие требования к механическим свойствам твердых тел. Например, широкое использование металлов связано с тем, что они обладают целым комплексом механических свойств: высокая прочность, твердость и упругость, и в то же время – хорошая пластичность и вязкость.

Если рассматривать твердые тела в отсутствие действия на них внешних сил, то в этом случае взаимное расположение различных частей тела должно отвечать состоянию механического равновесия.

Под действием внешней растягивающей нагрузки расстояние между атомами увеличивается, и равновесное расположение их в твердом теле нарушается. Это приводит к нарушению равенства сил притяжения и отталкивания и возникновению внутренних сил, стремящихся вернуть атомы в первоначальное положение. Величину этих сил, отнесенную к единице площади поперечного сечения кристалла, называют напряжением.

Механические свойства материала отражают его реакцию на внешнее воздействие, в частности на механическую деформацию, которая может выражаться в сжатии, растяжении, изгибе, кручении. Деформацией называется изменение объема или формы твердого тела без изменения его массы под действием внешних сил. Таким образом, механические свойства материала определяются силами связи, действующими между атомами или молекулами, составляющими твердое тело.

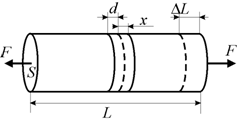
Пусть f − сила, которая возникает при растяжении тела между двумя частицами в нем. Рассмотрим стержень с поперечным сечением S и длиной L (рис. 4.1), к которому приложена растягивающая сила F. Эта сила изменяет расстояние между соседними атомными слоями на x и вызывает удлинение стержня на DL.

 

Рис. 4.1. К выводу закона Гука [74]

 

По третьему закону Ньютона эта сила уравновешивается внутренней силой .

,

(4.1)

где N – число частиц, находящихся в слое площадью S, а b − константа жесткости связи этих частиц. При этом в растянутом стержне возникает механическое напряжение

,

(4.2)

где .

Умножим и разделим правую часть выражения (4.2) на расстояние между атомными слоями d.

,

(4.3)

где  − величина, называемая модулем упругости, или модулем Юнга, а  - относительное изменение расстояния между атомными плоскостями в направлении действия внешней силы F. Умножим числитель и знаменатель в выражении для e на число атомных слоев (), располагающихся по всей длине стержня L

.

(4.4)

Следовательно, e представляет собой относительное удлинение образца, вызванное действием внешней силы.

Из формулы (4.3) видно, что до тех пор, пока выполняется гармоническое приближение, т. е. пока силы, возникающие при смещении частиц друг относительно друга вследствие деформации тела, остаются линейными функциями смещения, напряжения s будут пропорциональны относительной деформации

.

(4.5)

Формула (4.5) представляет собой закон Гука.

Установим, какой физический смысл имеет модуль Юнга B. Положим , тогда . Следовательно, модуль упругости численно равен напряжению, которое способно было бы вызвать растяжение образца на , если бы при этом закон Гука не нарушался и образец не разрушался. Ни один реальный материал, кроме резины, не способен выдержать таких деформаций.

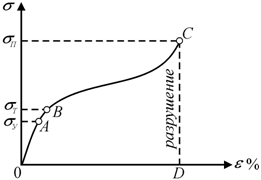
Для характеристики зависимости между механическими напряжениями s, которые возникают в твердом теле при приложении к нему внешней силы, и деформациями e используют диаграммы деформаций. Рассмотрим такую диаграмму в общем виде для одноосного растяжения цилиндрического образца (рис. 4.2).

Для малых относительных деформаций e имеет место линейная зависимость . Это означает, что на участке ОА деформация обратима, т. е. после снятия нагрузки форма и размеры образца восстанавливаются. При этом нагрузка должна прикладываться и сниматься достаточно быстро, иначе деформация становится необратимой. Явление развития деформации при длительном приложении внешней силы называется ползучестью материала. Прямолинейный участок ОА соответствует упругой деформации твердого тела. Для основной массы материалов относительная упругая деформация не превышает долей процента. Точка А на диаграмме отделяет ее линейную часть от нелинейной, а ее ордината  носит название предела упругости. За пределом области ОА начинается пластическая деформация.

 

Рис. 4.2. Диаграмма деформации

 

Значение  соответствует пределу текучести и представляет собой минимальное напряжение, при котором деформация продолжает возрастать без увеличения нагрузки, т. е. такое напряжение, при котором после прекращения действия внешней деформирующей силы наблюдается остаточная деформация. Кривая ВС отвечает области пластической деформации. При низких температурах величина остаточной деформации не зависит от времени приложения нагрузки. Деформацию, не зависящую от времени приложения нагрузки и сохраняющуюся после ее снятия, называют пластической деформацией. При достижении величины приложенного напряжения значения , соответствующего точке С диаграммы, наступает разрушение тела.

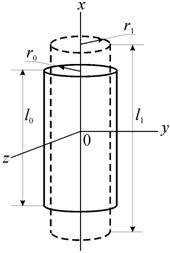
Закон Гука (4.5) называют элементарным, и справедлив он только для изотропных твердых тел. Однако в общем случае деформация может возникать и в направлениях, отличных от направления приложения силы. Например, при одноосном растяжении происходит сжатие в перпендикулярном направлении (рис 4.3). Поперечная деформация при упругом растяжении или сжатии характеризуется коэффициентом Пуассона m. Он равен отношению изменения размеров в поперечном направлении к изменению размеров в продольном направлении. Для большинства твердых тел значение коэффициента Пуассона находится в пределах .

 

Рис. 4.3. Изменение размеров при одноосном растяжении цилиндрического образца [74]

 

В соответствии со сказанным и с обозначениями на рис. 4.3 рассчитать значение коэффициента Пуассона можно по формуле

,

(4.6)

где  и  − соответственно радиус и длина цилиндрического образца до деформации растяжения, а  и  − после.