10.4. Концентрация носителей заряда для невырожденного и вырожденного электронного газа

Концентрация электронов в зоне проводимости равна:

.

(10.14)

Отметим, что в качестве верхнего предела в написанном интеграле необходимо было бы взять энергию верхнего края зоны проводимости. Но, т. к. функция f для энергий E > F экспоненциально быстро убывает с ростом энергии E, то замена верхнего предела на бесконечность не меняет значения интеграла. Подставив в (10.13) выражения (10.6) и (10.13), получим:

(10.15)

где

.

(10.16)

Величина N_C получила название эффективной плотности состояний в зоне проводимости.

В случае невырожденного полупроводника, когда уровень Ферми лежит выше потолка валентной зоны хотя бы на 2k_BT, т. е. F – E_C > 2k_BT, функция Ферми–Дирака для дырок f_p имеет вид:

,

(10.17)

а концентрация дырок в валентной зоне

,

(10.18)

где E_V – энергия, соответствующая потолку валентной зоны. Величина N_V  - эффективная плотность состояний в валентной зоне, рассчитывается по уравнению (10.16), если вместо эффективной массы электрона m_n взять эффективную массу дырки m_p..

Отметим, что в (10.14) перед интегралом появился множитель 2, что связано с тем, что на каждом уровне энергии могут находиться два электрона с противоположными спинами (принцип Паули).

Для расчета концентрации электронов n и дырок p по уравнениям (10.15) и (10.18) необходимо знать положение уровня Ферми F. Однако произведение концентраций электронов и дырок для невырожденного полупроводника не зависит от положения уровня Ферми, хотя зависит от температуры:

.

(10.19)

Это уравнение используется для расчета концентрации дырок  p при известной величине концентрации электронов n или, наоборот, для расчета концентрации n при известной концентрации p. Величина собственной концентрации n_i при комнатной и температуре жидкого азота для конкретных полупроводников приводится в литературе [72].
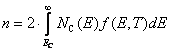