10.3. Функции распределения электронов по энергиям

10.3.1. Квантовая статистика Ферми−Дирака

Электроны, как частицы, обладающие полуцелым спином, подчиняются статистике Ферми–Дирака. Вероятность того, что электрон будет находиться в квантовом состоянии с энергией Е, выражается функцией Ферми–Дирака:

.

(10.12)

Здесь F – энергия Ферми, определяемая как значение энергии, при которой все состояния системы частиц, подчиняющихся статистике Ферми–Дирака заняты. Для электронного газа значение энергии Ферми совпадает со значением химического потенциала при T = 0 К и определяется как величина энергии, необходимая для изменения числа частиц в системе на единицу [79]. Также из формулы (10.12) видно, что энергию Ферми можно определить как энергию такого квантового состояния, вероятность заполнения которого равна 1/2.

Вид функции Ферми–Дирака схематически показан на рис. 10.6.

Рис. 10.6. Функция распределения плотности состояний в зоне проводимости N(E), функции Ферми–Дирака f1 (T1 = 0 К), f2 (T2 > 0 К), f3 (T3 > T2) и Больцмана fБ

 

 При Т = 0 К она имеет вид разрывной функции. Для энергии меньшей энергии Ферми E < F функция Ферми-Дирака равна 1, а значит, все квантовые состояния при E < F заполнены электронами. Для энергии большей энергии Ферми E > F функция f = 0 и соответствующие квантовые состояния не заполнены. При Т > 0 функция Ферми-Дирака изображается непрерывной кривой и в узкой области энергий, порядка нескольких k_BT, в окрестности точки E = F быстро изменяется от 1 до 0. Размытие функции Ферми-Дирака тем больше, чем выше температура.
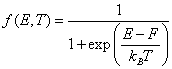