10.1. Плотность квантовых состояний в разрешенных зонах.
Классический 3D электронный газ
Стационарные состояния электрона в идеальном кристалле характеризуются квазиимпульсом р. Запишем принцип неопределенности Гейзенберга для квазиимпульсов px, py и pz:
|
|
(10.1) |
Перемножим соответственно левые и правые части этих соотношений. Получим
|
|
(10.2) |
где ![]() и
и ![]() . Таким образом,
. Таким образом, ![]() – это некоторый объем
в пространстве квазиимпульсов px, py, pz,
т. е. внутри зоны Бриллюэна, а DV – некоторый объем внутри полупроводника. Для расчета концентраций
носителей заряда (т. е. числа носителей в единице объема полупроводника)
выделим внутри кристалла единичный объем DV = 1 см3. Тогда из (10.2)
получим Dp ³ h3. Значит, внутри объема Dp в зоне Бриллюэна находится только одно квантовое состояние.
Следовательно, h3 – это объем одной «квартирки» в
зоне Бриллюэна, в которую по принципу Паули можно поместить два электрона с
разными спинами. Поэтому число квантовых состояний, соответствующее элементу
объема Dp в зоне
Бриллюэна и рассчитанное на единицу объема кристалла, равно Dp/h3, т. е. числу
«квартирок» в объеме Dp. При заполнении зоны проводимости электронами заполняются
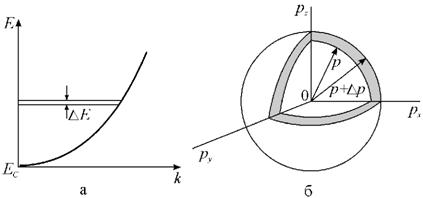
вначале самые нижние уровни. Зона проводимости одномерна относительно энергии
(рис. 10.1, а).
Зона Бриллюэна – трехмерна (px, py, pz) (рис. 10.1, б). В дальнейшем
для выполнения интегрирования перейдем от конечных приращений Dp к дифференциалам dp. Внутри тонкого
сферического слоя радиусом p и толщиной dp число квантовых состояний будет равно
– это некоторый объем
в пространстве квазиимпульсов px, py, pz,
т. е. внутри зоны Бриллюэна, а DV – некоторый объем внутри полупроводника. Для расчета концентраций
носителей заряда (т. е. числа носителей в единице объема полупроводника)
выделим внутри кристалла единичный объем DV = 1 см3. Тогда из (10.2)
получим Dp ³ h3. Значит, внутри объема Dp в зоне Бриллюэна находится только одно квантовое состояние.
Следовательно, h3 – это объем одной «квартирки» в
зоне Бриллюэна, в которую по принципу Паули можно поместить два электрона с
разными спинами. Поэтому число квантовых состояний, соответствующее элементу
объема Dp в зоне
Бриллюэна и рассчитанное на единицу объема кристалла, равно Dp/h3, т. е. числу
«квартирок» в объеме Dp. При заполнении зоны проводимости электронами заполняются
вначале самые нижние уровни. Зона проводимости одномерна относительно энергии
(рис. 10.1, а).
Зона Бриллюэна – трехмерна (px, py, pz) (рис. 10.1, б). В дальнейшем
для выполнения интегрирования перейдем от конечных приращений Dp к дифференциалам dp. Внутри тонкого
сферического слоя радиусом p и толщиной dp число квантовых состояний будет равно
|
|
(10.3) |
|
|
|
Рис. 10.1. Диаграмма для расчета плотности квантовых состояний: а - распределение электронов по
энергии в зоне проводимости; б - зона Бриллюэна
для расчета плотности состояний |
Определим число квантовых состояний в зоне проводимости в узком интервале энергий от Е до Е + dЕ, рассчитанное на единицу объема кристалла. Его можно представить в виде N(E)dE, где N(E) есть плотность состояний.
Для существенного ряда кинетических и оптических эффектов в полупроводниках являются важными характеристики плотности квантовых состояний вблизи экстремумов в зависимости E(k), т. е. выше дна зоны проводимости и ниже потолка валентной зоны.
Вблизи дна зоны проводимости для случая изотропного параболического закона дисперсии энергия электрона
|
|
(10.4) |
где ЕC – энергия, соответствующая дну зоны проводимости. Для
удобства эффективную массу электрона mn будем писать без звездочки. Из (10.4) получим ![]() , т. е.
, т. е. ![]() и
и ![]() . Подставляем в (10.3), имеем
. Подставляем в (10.3), имеем
|
|
(10.5) |
Отсюда
|
|
(10.6) |
Аналогичная формула получается и для валентной зоны, но только вместо (Е – ЕC) напишем (ЕV – Е), а вместо mn – эффективную массу дырки mp.
Как видно из (10.6), плотность квантовых состояний возрастает по мере удаления от дна зоны проводимости.
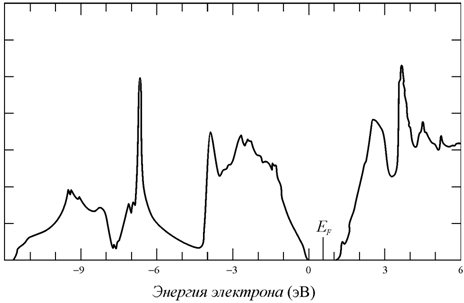
Соотношение (10.6) получено из первых принципов и не описывает реальную плотность квантовых состояний в зонах разрешенных энергий вдали от дна зоны проводимости ЕC и потолка валентной зоны ЕV. Для точного расчета зависимости N(E) необходим учет анизотропии кристалла, потенциала взаимодействия атомных остовов, вид перекрывающихся волновых функций. На рис. 10.2 показана полученная экспериментальным методом плотность электронных состояний в разрешенных зонах кремния с собственной проводимостью. Видно, что наблюдается зависимость роста плотности состояний с ростом энергии вглубь зоны проводимости и валентной зоны. В то же время зависимость N(E) в глубине разрешенных зон носит более сложный характер, чем монотонная корневая зависимость от энергии согласно (10.6).
|
|
|
Рис. 10.2. Плотность электронных состояний в разрешенных зонах кремния с собственной проводимостью |