Диоды Ганна
Диоды Ганна – это функциональные приборы, которые
реализуют определённую функцию. В частности диод Ганна реализует функцию
генератора СВЧ – колебаний.
Впервые
явление было открыто Ганном в 1963 г.
Диод Ганна –
это объёмный материал на основе GaAs, который при приложении к
нему постоянного напряжения в определённом диапазоне, генерирует СВЧ –
колебания.
Рис 1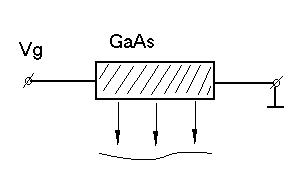
Причинной
возникновения СВЧ – колебаний, является наличие на ВАХ, участка с отрицательным
дифференциальным сопротивлением (ОДС).
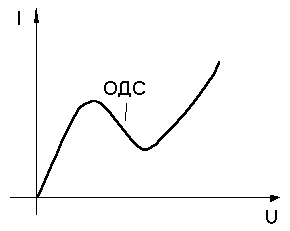
Рис 2
Зонная диаграмма и ВАХ GaAs.
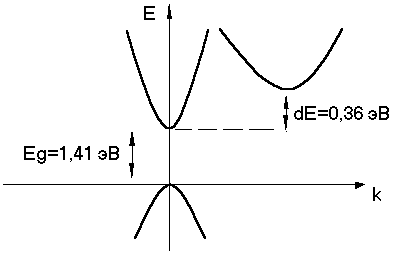
GaAs
– как полупроводник
Рис 3
Эффективная масса m1*=0,07m0 m1*=1,2m0
Подвижность µ1=600 см2/В*с µ2=150 см2/В*с
По мере роста приложенного
напряжения к образцу GaAs дополнительная
энергия, которую приобретают электроны, расположенные в основном минимуме
(нижняя долина), возрастает и начинает приближаться к энергии междолинного расщепления.
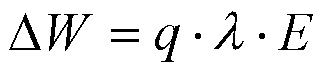
Электрон начинает перебираться из
основного минимума к дополнительному (верхняя долина).
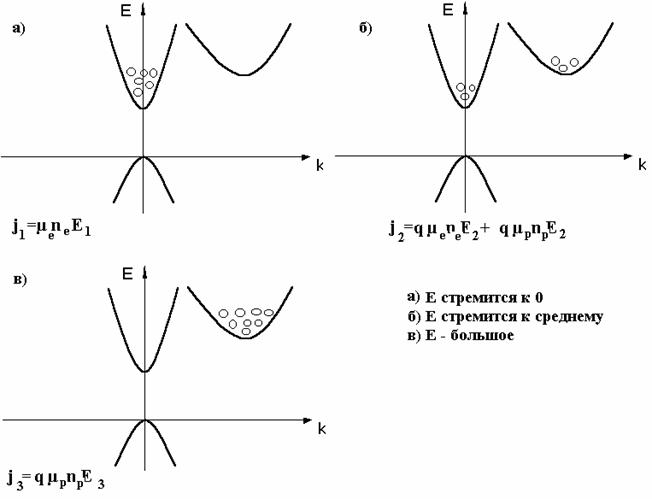
Рис 4
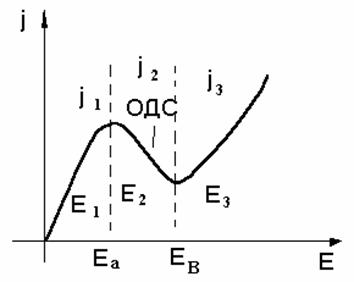
Вольт – Амперная Характеристика (ВАХ).
Рис 5
В следствии
того, что подвижности µ1 и µ2 отличаются сильно, на участке ВАХ проявляется
участок с ОДП.
Для GaAs – характерные точки между которыми происходит перераспределение Еа и Ев
Еа=3,2 кВ/см Ев=20 кВ/см
Так как в GaAs энергия
расщепления меньше ширины запрещённой зоны ![]() E<Eg, то Ев меньше напряжения лавинного
пробоя Елп (Ев<Елп).
E<Eg, то Ев меньше напряжения лавинного
пробоя Елп (Ев<Елп).
Механизм междолинных переходов приводящих к появлению участка с ОДС,
часе всего называют эффектом Ганна.
Такой эффект
реализуется в очень малом количестве полупроводников.
Рис 6
Если подвижности µ1, µ2 мало
отличаются друг от друга, то на ВАХ
появляется характеристика без
ОДС.
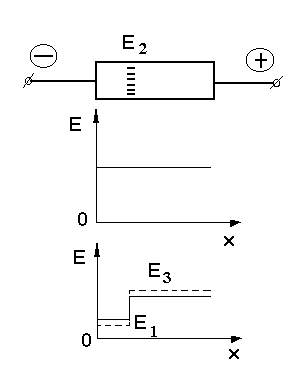
Зарядовая
неустойчивость в структурах с ОДС.
Рис 7
При выборе рабочей точки на
участке ОДС любая зарядовая неустойчивость будет расти. Например, если в какой
– то точке увеличивается отрицательный заряд, это приведёт к уменьшению поля
слева от него и увеличивается поле справа от него, но при этом ток слева увеличивается,
а справа уменьшается. И объёмный заряд будет расти. И это будет происходить до
тех пор, пока заряд не вырастет на столько, что поле Е1 и Е3 соответствующие одинаковым токам. После этого рост
зарядовой неустойчивости прекратится и, но она будет двигаться по образцу.
В
момент выхода объёмного заряда из образца возникает скачок тока и ясно, что
время пролёта через образец – есть время
соответствующее периоду колебаний тока во внешней цепи.
В случае если ВАХ не имеет участка с ОДС, то зарядовая неустойчивость,
вызывающая изменение электрических полей, сама по себе рассасывается.
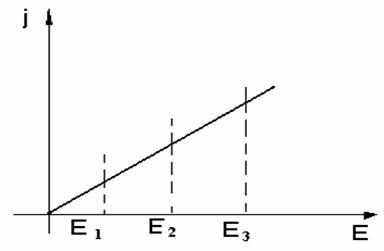
Рис 8
Домены сильного
электрического поля в диодах Ганна.
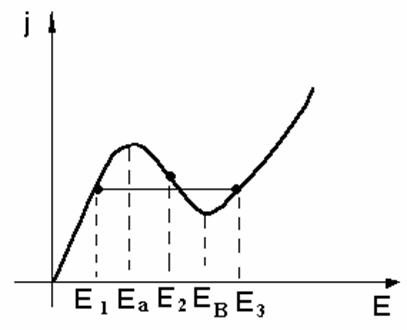
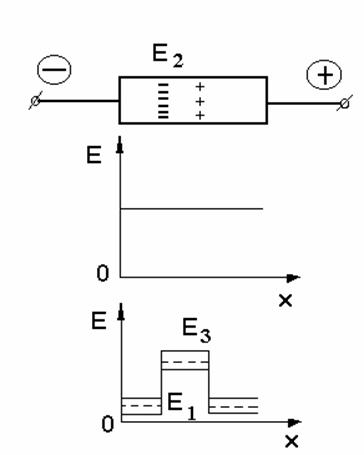
Рис 9
Рис 10
В GaAs флуктуации приводят к
образованию сильного электрического поля, заряд в котором растёт до тех пор,
пока токи слева и справа внутри домена не выровняются. Причём внутри домена
будут только тяжёлые электроны, а снаружи вне домена – лёгкие электроны. Этот
домен электрического поля также движется по образцу и его
разрушение на контактах будет соответствовать появлению колебаний тока в
цепи.
Временные параметры диодов Ганна.
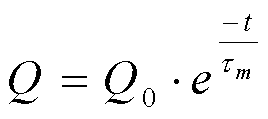
![]()
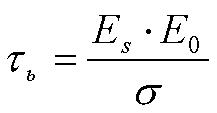
Q - заряд
![]() - время
релаксации относительно носителей.
- время
релаксации относительно носителей.
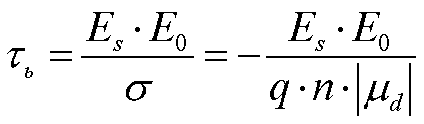
Если мы находимся на участке ОДС,
то ![]() будет
отрицательной и заряд будет не рассасываться, а формироваться.
будет
отрицательной и заряд будет не рассасываться, а формироваться.
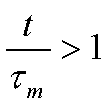
- Условие формирования, а не рассасывания
заряда
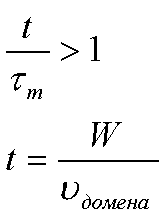 Из них
следует
Из них
следует
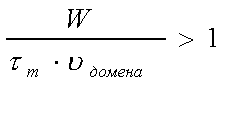
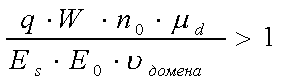
То есть, эта формула
эта формула
есть условие конструирования
диодов Ганна из GaAs.
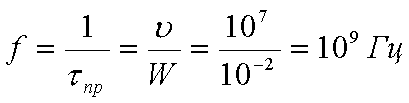
W=0,1 мм
![]() =107
=107
Статистическая ВАХ
GaAs.
Отсюда следует
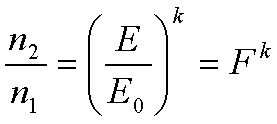
Экспериментально установлено, что для GaAs k=4
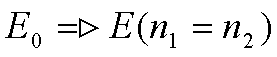

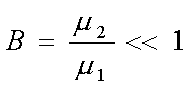

Соотношение, описывающее ВАХ в диодах Ганна на основе GaAs
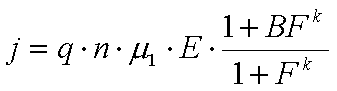

Рис 11
Диоды Ганна
Приборы на эффекте междолинного
перехода электронов.
В
1963 г. Ганн установил, что при наложении постоянного электрического поля, с
напряжённостью выше некоторого порогового значения, на монокристаллический
образец из арсенида галлия или фосфида индия его сопротивление начинает
периодически изменяться с частотой, лежащей в СВЧ - диапазоне. В результате в
цепи, в которую включён такой образец, возникает переменный ток СВЧ -
диапазона. Причем частота изменения тока равняется величине, обратной времени
пролёта электронов от катода до анода. В дальнейшем было показано, что
генерация переменного тока обусловлена эффектом междолинного
перехода электронов, стимулированного сильным электрическим током.
Междолинный переход электронов
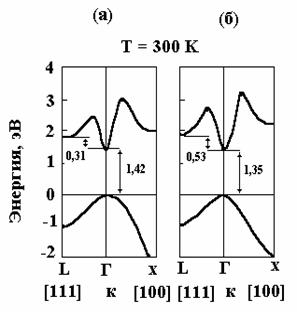
Эффект междолинного перехода рассмотрим на примере арсенида галлия
и фосфида индия, структура энергетических зон которых
представлена на рис
[1]. При малой напряжённости электрического поля в образце все
электроны находятся в нижней долине зоны проводимости, расположенной в точке Г (рис [1]).
Здесь они обладают малой
эффективной массой и высокой подвижностью. Если напряжённость поля достигнет
некоторой пороговой величины (Еп), то появятся горячие электроны, способные
перейти в верхнюю долину зоны проводимости, расположенную в точке L. Дальнейшее увеличение Е будет сопровождаться непрерывным
ростом концентрации электронов в верхней долине. При переходе в верхнюю долину
эффективная масса электронов значительно возрастает, а подвижность падает.
Следовательно, скорость дрейфа
электронов по мере увеличения Е при Е>Еп должна уменьшаться. Это приведёт к
появлению на вольт - амперной характеристике образца участка с отрицательным
дифференциальным сопротивлением (ОДС).
Для
получения зависимости ![]() от E
введём следующие обозначения:
от E
введём следующие обозначения:
m1* и m2*
- эффективные массы
k1 и k2
- подвижности
n1 и n2- концентрации электронов в нижней и верхней долинах
соответственно.
Из
выражения для плотности тока в образце при Еп>Е
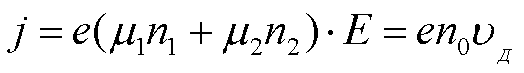 (1)
(1)
с учётом того, что n0 = n1 + n2,
получим
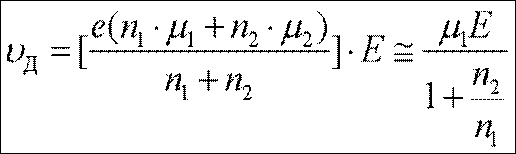 (2)
(2)
так как k1 >> k2. Будем считать, что
электронные температуры (Те)
в обеих долинах одинаковы. Тогда, исходя из статистики Максвелла - Больцмана,
можно записать следующее выражение для отношения заселённостей электронами
верхней и нижней долин:
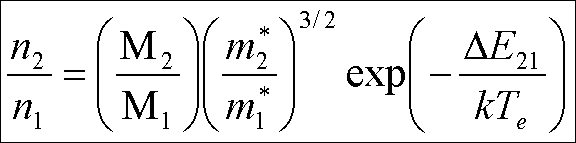 (3)
(3)
где предэкспоненциальный
множитель определяет отношение плотностей состояний в долинах, а М1
и М2 - число верхних и
нижних долин соответственно.
Для
GaAS M1=1, M2=4, m1*=0,067m0, m2*=0,55m0 и (M2/M1)(m2*/m1*)3/2=94.
Из (2) и (3) имеем
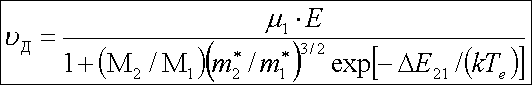 (4)
(4)
Выражение
для Те получим, используя условие
баланса энергии, приобретаемой электронами в электрическом поле в единицу
времени и теряемой в это же время за счёт столкновений:
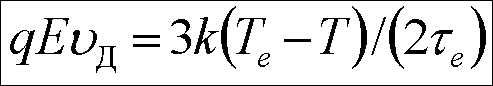 (5)
(5)
где ![]() - время релакса
энергии (порядка 10-12 с)
- время релакса
энергии (порядка 10-12 с)
Подстановка
(4)
в (5)
приводит к следующему выражению
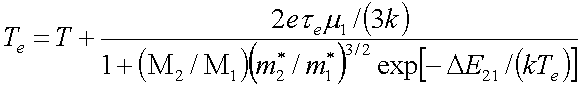 (6)
(6)
Отсюда можно рассчитать
зависимость Те от Е при любой температуре.
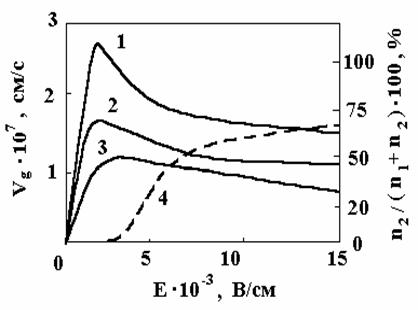

Зависимости ![]() от Е для GaAs рассчитанные с помощью (4) и (6) приведены на рисунке [2].
от Е для GaAs рассчитанные с помощью (4) и (6) приведены на рисунке [2].
Здесь же штриховой линией
показана зависимость заселённости верхней долины от Е. Из результатов расчёта
следует, что пороговое значение напряжённости поля увеличивается с ростом
температуры (см рис [2]). Кроме того, при достаточно высокой
температуре должен исчезать участок ВАХ с ОДС, так как в этом случае показатель
экспоненты в (4)
мал даже в области слабых полей, когда Те~Т, и поэтому экспонента меняется незначительно
при увеличении Е и
Те. Но тогда как следует из (4), ![]() ~ Е, то есть выполняется закон Ома.
Фактически это означает, что при высоких температурах заселённость электронами
верхней долины велика даже в области слабых полей и практически не изменяется,
с увеличением Е. Такая же картина будет реализовываться при малых значениях dЕ1,2.
Таким образом, участок ОДС на ВАХ полупроводника может возникнуть за счёт междолинных переходов только при достаточно низких
температурах, когда большинство электронов находится в основном минимуме зоны
проводимости.
~ Е, то есть выполняется закон Ома.
Фактически это означает, что при высоких температурах заселённость электронами
верхней долины велика даже в области слабых полей и практически не изменяется,
с увеличением Е. Такая же картина будет реализовываться при малых значениях dЕ1,2.
Таким образом, участок ОДС на ВАХ полупроводника может возникнуть за счёт междолинных переходов только при достаточно низких
температурах, когда большинство электронов находится в основном минимуме зоны
проводимости.
Из
(4)
также следует, что плотность состояний в основном минимуме зоны проводимости
должна быть мала, а в побочном - велика. В противном
случае член с экспонентой в (4) будет значительно меньше единицы и не сможет эффективно
влиять на величину ![]() .
И наконец необходимо отметить, что dЕ1,2 должно быть меньше ширины запрещённой зоны
полупроводника, чтобы величина порогового поля не оказалась сравнимой с
напряжённостью поля лавинного пробоя. Требование к резкому
неравенству подвижностей электронов в основной и побочной долинах является
очевидным.
.
И наконец необходимо отметить, что dЕ1,2 должно быть меньше ширины запрещённой зоны
полупроводника, чтобы величина порогового поля не оказалась сравнимой с
напряжённостью поля лавинного пробоя. Требование к резкому
неравенству подвижностей электронов в основной и побочной долинах является
очевидным.
В
заключение отметим, что эксперимент хорошо подтверждает расчёт и даёт следующие
значения для параметров, характеризующих ВАХ образцов из арсенида галлия и
фосфида индия соответственно:
напряжённость
порогового поля - 3,2 * 103
и 10,5*103 В/см
максимальная
величина дрейфовой скорости - 2,2*107 и 2,5*107 см/с
максимальная величина отрицательной дифференциальной подвижности -
2400 и 2000 см2.(В*с).
Диоды Ганна
Дипольные домены и
возможные
режимы работы диодов
Ганна.
Анализ
механизма возникновения периодических изменений сопротивления образца с ОДС
проведём на примере однородно легированного полупроводника с омическими
контактами, в котором приложенная разность потенциалов создаёт электрическое
поле Е=Еп Предположим, что в некоторый момент времени вследствие
тепловой флуктуации группа электронов сместилась в сторону катода относительно
неподвижно ионизованных доноров (рис [3], а). Тогда возникшая таким образом
избыточная концентрация электронов (рис [3], б) должна изменятся во времени с
известным соотношением
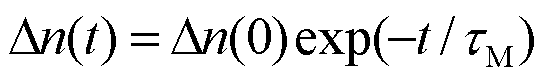 (7)
(7)
представляющим собой закон
релаксации основных носителей заряда в полупроводнике. Если в рассматриваемом
образце справедлив закон Ома, то время релаксации Максвелла 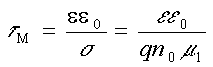 . В
противном случае
. В
противном случае ![]() следует заменить на
дифференциальную удельную проводимость и для образца с ОДС
следует заменить на
дифференциальную удельную проводимость и для образца с ОДС
 (8)
(8)
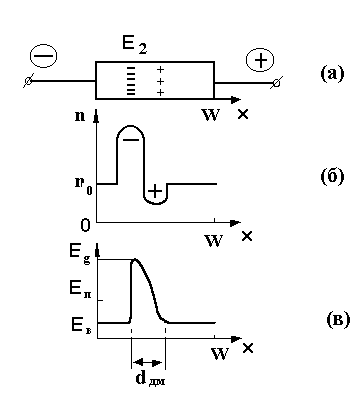

где µ- - отрицательная
дифференциальная подвижность, соответствующая падающему участку ВАХ. Из (7) и (8)
следует, что в образце с ОДС первоначальная тепловая флуктуация концентрации
электрона должна не убывать с ростом t, а увеличиваться, так
как µ-<0.
Этот факт
объясняется следующими обстоятельствами. В области возникшего дипольного объёмного заряда напряжённость электрического
поля, как это следует из уравнения Пуассона, возрастает и станет больше
порогового значения, а в остальной части образца Е слегка уменьшится и станет меньше Еп (рис [3], в), так как напряжения,
подаваемое на образец, поддерживается постоянным. В результате этого дрейфовая
скорость электронов и плотность тока в области существования объёмного заряда
уменьшается, а в остальной части образца изменятся незначительно. Это приведёт
к дальнейшему увеличению концентрации электронов в левой части объёмного заряда
(за счёт их подтока от катода) и концентрации некомпенсированных доноров в
правой части его. Этот процесс увеличения dn и dNd+ прекратится и дипольный
слой достигнет стабильной конфигурации, когда плотность тока внутри и вне его
станет одинаковой и будет соответствовать точкам ВАХ, лежащим вне участка ОДС (рис [4], например,
точки Е=Ев и Е=Ед). Спад силы тока в цепи при
формировании диполя или домена сильного поля обусловлен резким уменьшением
подвижности электронов в нём и, следовательно, увеличением сопротивления
образца. Логично предположить, что наиболее стабильное состояние домена
соответствует минимальной мощности, потребляемой образцом от источника питания,
то есть, когда плотность тока в образце имеет наименьшее
возможное значение - ![]() (см рис [4]). Тогда максимальная напряжённость поля
внутри домена сильного поля будет равняться Ед,
а вне его - Ев (см рис [3],в и [4]).
(см рис [4]). Тогда максимальная напряжённость поля
внутри домена сильного поля будет равняться Ед,
а вне его - Ев (см рис [3],в и [4]).
![]()
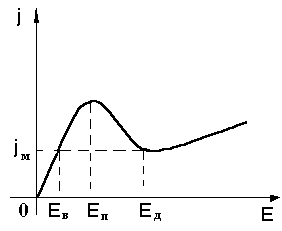
Ширину или
толщину домена (dдм) можно оценить исходя из
того, что падение напряжения на образце до и после образования домена одно и то
же, то есть
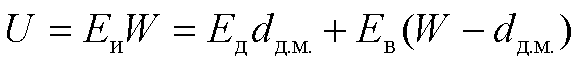 (9)
(9)
где исходная напряжённость поля Еи ~ Еп.
Из (9)
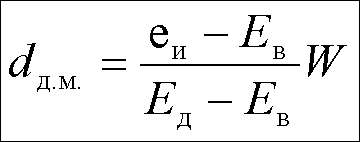 (10)
(10)
Распределение
напряжённости электрического поля в домене, как показывает решение уравнения
Пуассона, зависит от концентрации электронов в данном образце. При больших n0 максимум Е располагается в центре домена и
зависимость Е от x имеет симметричный вид. Если n0 мало, то кривая ![]() принимает форму, близкую к прямоугольному
треугольнику ( см рис [3], в).
принимает форму, близкую к прямоугольному
треугольнику ( см рис [3], в).
В процессе
формирования и после его окончания дипольный домен дрейфует от катода к аноду.
Если предположить, что домен возникает у катода за счёт имеющейся здесь
неоднородности в распределении примеси (пониженное значение Nd и повышенная
напряжённость поля), то за время пролёта
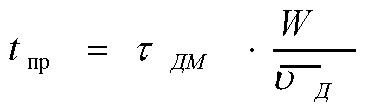 (11)
(11)
где ![]() - некоторая средняя скорость дрейфа домена, он
достигнет анода и исчезнет, после чего в образце восстановится однородное
распределение поля и первоначальное (до формирования домена) значение тока.
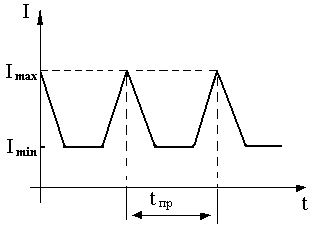
Затем за счёт тепловой флуктуации у катода начнёт формироваться следующий домен
и т. д. Периодически повторяющиеся процессы формирования домена у катода и
рассасывания его у анода приведут к соответствующему изменению сопротивления
образца и силы тока (рис [5]).
- некоторая средняя скорость дрейфа домена, он
достигнет анода и исчезнет, после чего в образце восстановится однородное
распределение поля и первоначальное (до формирования домена) значение тока.
Затем за счёт тепловой флуктуации у катода начнёт формироваться следующий домен
и т. д. Периодически повторяющиеся процессы формирования домена у катода и
рассасывания его у анода приведут к соответствующему изменению сопротивления
образца и силы тока (рис [5]).

Для
того чтобы первоначальная тепловая флуктуация концентрация электронов заметно
возросла, необходим интервал времени, превосходящий - ![]() (см (7)). Отсюда следует, что
периодическое изменение силы тока через образец будет возникать лишь в том
случае, когда
(см (7)). Отсюда следует, что
периодическое изменение силы тока через образец будет возникать лишь в том
случае, когда ![]() или в соответствии с (11) и (8)
или в соответствии с (11) и (8)
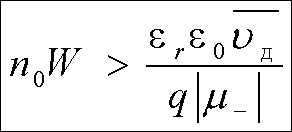 (12)
(12)
Это неравенство иногда называют
критерием Кремера. Не останавливаясь на методах оценки ![]() ,
отметим, что после подстановки всех величин в правую часть (12) для
арсенида галлия и фосфида индия получается величина порядка 1012 см-2.
,
отметим, что после подстановки всех величин в правую часть (12) для
арсенида галлия и фосфида индия получается величина порядка 1012 см-2.
Режим
работы диода на эффекте междолинного перехода
электронов ( или диода Ганна), при котором уверенно
выполняется неравенство
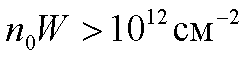 (13)
(13)
называется пролётным режимом. Для
его реализации необходимо включить диод в параллельную резонансную цепь,
например в СВЧ - резонатор с высокой добротностью, настроенный на пролётную
частоту ![]() .
Отметим, что в пролётном режиме на кривой зависимости тока от времени будут
наблюдаться резкие всплески (см рис [5]), если длина образца
значительно превышает длину домена. Для получения формы колебаний тока, близкой
к синусоидальной, необходимо уменьшать длину образца
или увеличивать ширину домена. Последнее можно
реализовать, уменьшая концентрацию электронов (n0)
в образце.
.
Отметим, что в пролётном режиме на кривой зависимости тока от времени будут
наблюдаться резкие всплески (см рис [5]), если длина образца
значительно превышает длину домена. Для получения формы колебаний тока, близкой
к синусоидальной, необходимо уменьшать длину образца
или увеличивать ширину домена. Последнее можно
реализовать, уменьшая концентрацию электронов (n0)
в образце.
При работе диода в резонаторе к нему кроме
постоянного внешнего смещения оказывается приложенным также СВЧ - поле,
возникающее в резонаторе за счёт колебания тока, протекающего через диод.
Предположим, что СВЧ - поле меняется во времени по гармоническому закону, а
резонатор настроен на частоту выше пролётной ![]() .
Тогда при достаточно большой амплитуде СВЧ - поля дипольный момент в образце
может рассосаться, не доходя до анода. Для этого необходимо, чтобы в
полупериод, когда векторы напряжённости постоянного и СВЧ - поля
противоположны, суммарная напряжённость поля была бы меньше некоторой величины,
а длительность полупериода была бы больше
.
Тогда при достаточно большой амплитуде СВЧ - поля дипольный момент в образце
может рассосаться, не доходя до анода. Для этого необходимо, чтобы в
полупериод, когда векторы напряжённости постоянного и СВЧ - поля
противоположны, суммарная напряжённость поля была бы меньше некоторой величины,
а длительность полупериода была бы больше![]() ,
соответствующего положительной подвижности. С точностью до численного
коэффициента последнее условие можно записать так:
,
соответствующего положительной подвижности. С точностью до численного
коэффициента последнее условие можно записать так: 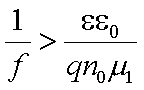 .
или
.
или
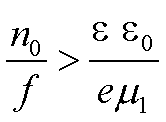 (14)
(14)
Для GaAs и InP ![]() .
Неравенство (14)
является условием реализации режима работы диода с подавлением домена. В этом
режиме в каждый “положительный” полупериод СВЧ - поля в диоде Е>Еп
и у катода зарождается домен, а в каждый “отрицательный” полупериод он
рассасывается на пути к аноду. Таким образом, генерация переменного тока в этом
случае происходит на частоте, определяемой параметрами резонансной цепи.
.
Неравенство (14)
является условием реализации режима работы диода с подавлением домена. В этом
режиме в каждый “положительный” полупериод СВЧ - поля в диоде Е>Еп
и у катода зарождается домен, а в каждый “отрицательный” полупериод он
рассасывается на пути к аноду. Таким образом, генерация переменного тока в этом
случае происходит на частоте, определяемой параметрами резонансной цепи.
Если
обеспечить одновременное выполнение двух неравенств:
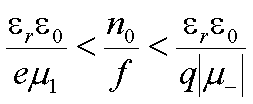 (15)
(15)
то диод Ганна будет работать в
режиме ограниченного накопления объёмного заряда. Для GaAs и InP из (15) следует что ![]() .
Поскольку в (15) период СВЧ – сигнала меньше
.
Поскольку в (15) период СВЧ – сигнала меньше ![]() ,
соответствующего отрицательной дифференциальной подвижности, то в полупериод,
когда Е>Еп,
домен сильного поля не успевает полностью сформироваться, а в следующий
полупериод (Е<Еп)
он полностью рассасывается. При этом будет наблюдаться возрастание
сопротивления образца в один полупериод СВЧ – сигнала и спад его в другой, что
и вызывает эффективную генерацию мощности на частоте, определяемой параметрами
внешней цепи.
,
соответствующего отрицательной дифференциальной подвижности, то в полупериод,
когда Е>Еп,
домен сильного поля не успевает полностью сформироваться, а в следующий
полупериод (Е<Еп)
он полностью рассасывается. При этом будет наблюдаться возрастание
сопротивления образца в один полупериод СВЧ – сигнала и спад его в другой, что
и вызывает эффективную генерацию мощности на частоте, определяемой параметрами
внешней цепи.
Диоды Ганна
Режим с обогащенным слоем
Этот режим
соответствует случаю, когда не выполняется условие (12),
следовательно, домен сильного поля не успевает сформироваться, доменная
неустойчивость не возникает и образец не является генератором. При однородном
распределении концентрации носителей вдоль образца (n0
y не зависит от x) его ВАХ в соответствии с (1) повторяла бы зависимость ![]() от Е (рис [2]).
Однако в реальных случаях катод (обычно контакт n+-n-типа) инжектирует в образец электроны, что приводит к
совершенно иному виду ВАХ.
от Е (рис [2]).
Однако в реальных случаях катод (обычно контакт n+-n-типа) инжектирует в образец электроны, что приводит к
совершенно иному виду ВАХ.
Из условия
непрерывности тока в образце следует, что там, где концентрация носителей
заряда выше, напряжённость поля должна быть меньше. Полагая в первом
приближении, что у катода, инжектирующего электроны, Е=0 и численно решая систему уравнений
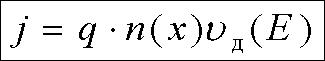 (16)
(16)
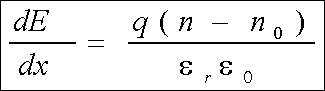 (17)
(17)
получим распределение
напряжённости поля и концентрации электронов вдоль образца, которые качественно
представлены на рис [6] . Если напряжённость
поля всюду меньше Еп,
то в большей части образца она слабо зависит от х (рис
[6], а, кривая 1), а концентрация электронов вдали от катода равна
равновесной (рис [6], б, кривая 1).
Как только
в некоторой точке Е станет больше Еп, скорость дрейфа электрона здесь уменьшится и
соответственно должна увеличиваться их концентрация, чтобы сила тока при любом х оставалась
постоянной. Подток избыточных электронов от катода в данную точку вызовет
увеличение плотности избыточного заряда и dE/dx [(см 17)]. Во всех
остальных точках, расположенных правее рассматриваемой, сила тока также
поддерживаться постоянной за счёт роста n(x) и dE/dx (рис [6], а и б, кривые 2).
Причём как следует из (16) и (17), чем выше плотность тока, тем больше должно быть
dE/dx, то есть
нелинейность кривой, изображающей зависимость Е от х, должна увеличиваться (рис [6], а, кривые 2,3). В этой области образца, где Е<Еп, ![]() и концентрация электронов уменьшается с ростом
х.
и концентрация электронов уменьшается с ростом
х.
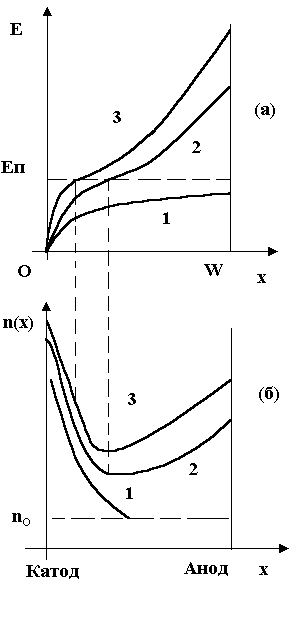

ВАХ таких образцов при Е<Еп
подчиняется закону Ома (рис [7]), а затем ток
практически выходит на насыщение, если равновесная концентрация электронов не
очень мала.
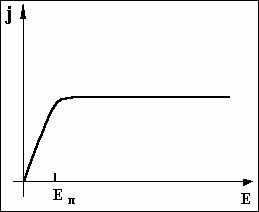

Если же n0 меньше некоторой величины при фиксированной длине
образца, то на ВАХ вслед за линейным должен наблюдаться участок,
соответствующий току, ограниченному пространственным зарядом. Таким образом, в
реальных образцах за счёт инжекции электронов с катода и подтока их к области с
пониженной подвижностью, где Е>Еп, на ВАХ исчезает участок с ОДС. У анода
таких образцов, как видно из рис [6], существует статический (неподвижный) домен
сильного электрического поля с повышенной концентрацией электронов. Иногда
такой домен называют статическим доменом обогащённого слоя.
Нарисованная
выше картина реализуется при наличие лишь постоянного
напряжения на образце. Стационарное неоднородное
распределение электрического поля и концентрации электронов вдоль образца,
приводящее к исчезновению участка ВАХ с ОДС, устанавливается приблизительно за
время пролёта (см. (11)). Поэтому если к диоду
кроме постоянного смещения приложить ещё и малое переменное поле с частотой,
близкой к пролётной ( ![]() ), то объёмный заряд не будет успевать
стабилизировать образец. В этом случае небольшая флуктуация объёмного заряда,
появившаяся у катода за счёт наличия переменного поля, будет нарастать по мере
продвижения к аноду, что приведёт к усилению переменного сигнала. Следовательно, такой диод будет играть роль усилителя СВЧ – сигнала
с частотой, совпадающей с пролётной или с ей гармониками. Эксперимент
подтверждает наличие отрицательной активной проводимости на соответствующих
частотах для образцов арсенида галлия, у которых n0W<1012 см-2.
), то объёмный заряд не будет успевать
стабилизировать образец. В этом случае небольшая флуктуация объёмного заряда,
появившаяся у катода за счёт наличия переменного поля, будет нарастать по мере
продвижения к аноду, что приведёт к усилению переменного сигнала. Следовательно, такой диод будет играть роль усилителя СВЧ – сигнала
с частотой, совпадающей с пролётной или с ей гармониками. Эксперимент
подтверждает наличие отрицательной активной проводимости на соответствующих
частотах для образцов арсенида галлия, у которых n0W<1012 см-2.
Мощность и КПД диодов Ганна
СВЧ –
мощность, генерируемую диодом Ганна, можно представить как 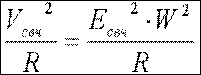 , где R –
сопротивление диода. В пролётном режиме работы
, где R –
сопротивление диода. В пролётном режиме работы 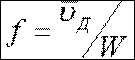 и
и ![]() .
Это соотношение между мощностью и частотой сопровождается экспериментом для
диодов из GaAs и InP. Для диодов из GaAs с достаточно длинной
базой при подаче импульсного смещения получена максимальная СВЧ – мощность
порядка 6 кВт на частоте около 2 ГГц. В непрерывном режиме работы, когда на
диод подаётся постоянное напряжение смещения, на частоте 10 ГГц СВЧ – мощность
равна приблизительно 2 Вт.
.
Это соотношение между мощностью и частотой сопровождается экспериментом для
диодов из GaAs и InP. Для диодов из GaAs с достаточно длинной
базой при подаче импульсного смещения получена максимальная СВЧ – мощность
порядка 6 кВт на частоте около 2 ГГц. В непрерывном режиме работы, когда на
диод подаётся постоянное напряжение смещения, на частоте 10 ГГц СВЧ – мощность
равна приблизительно 2 Вт.
Как следует из
оценок, верхний предел рабочей частоты диодов Ганна составляет примерно 150
ГГц. Он определяется инерционностью процесса передачи энергии электрического
поля электронам и процесса перехода последних из
основного минимума зоны проводимости в побочные. Реально достигнутая частота
генерации порядка 100 ГГц. Оценки также показывают, что в пролётном режиме
работы максимально достижимая величина КПД диодов Ганна составляет 10%, а в
режиме с разрушением домена – 13%.
В заключение
отметим, что конкретный вид ВАХ диода Ганна, его режим работы, СВЧ – мощность и
КПД существенным образом зависят от условий на контактах и от профиля
распределения примеси в активной области.
