1.4. Электропроводность полупроводников.
1.4.1. Особенности энергетических зон металлов, полупроводников и диэлектриков. Концентрация электронов и дырок в собственном полупроводнике.
 В металлах валентная зона заполнена не полностью (они обладают низкой валентностью) рис. 4, в результате чего валентные
электроны могут свободно перемещаться между атомами и соответственно концентрация свободных электронов чрезвычайно велика.
Энергетический уровень, разделяющий заполненную и свободную части зон в металле называют уровнем Ферми (в действительности
это поверхность). Формально уровень Ферми (F) можно определить как энергетический уровень, вероятность заполнения которого
равна ½. Ниже этого уровня преобладают электроны, выше преобладает свободное пространство (дырки).
В металлах валентная зона заполнена не полностью (они обладают низкой валентностью) рис. 4, в результате чего валентные
электроны могут свободно перемещаться между атомами и соответственно концентрация свободных электронов чрезвычайно велика.
Энергетический уровень, разделяющий заполненную и свободную части зон в металле называют уровнем Ферми (в действительности
это поверхность). Формально уровень Ферми (F) можно определить как энергетический уровень, вероятность заполнения которого
равна ½. Ниже этого уровня преобладают электроны, выше преобладает свободное пространство (дырки).

Рис 4. Энергетическая диаграмма металла.
 Полупроводники и диэлектрики отличаются шириной запрещенной зоны. В полупроводниках, как правило, запрещенная зона меньше
и не превышает 3 эВ, поэтому для полупроводников вероятность разрыва валентных связей за счет теплового нагрева значительно
больше, чем у диэлектриков и даже при комнатной температуре полупроводники могут обладать конечной электронной
проводимостью. При этом собственная концентрация носителей заряда от ширины запрещенной зоны и температуры. Уровень Ферми
в собственных полупроводниках и диэлектриках лежит в середине запрещенной зоны. В отличие от металлов в идеальных
собственных полупроводниках в середине зоны разрешенных уровней нет и соответственно не может быть электронов с такими
энергиями, однако если бы они были, то вероятность их заполнения была бы равна ½. Т.е. и в этом случае он указывает
на то какие состояния могут быть заполнены электронами, а какие нет. Действительно валентная зона ниже уровня Ферми - она
заполнена электронами, зона проводимости выше уровня Ферми, вероятность ее заполнения электронами fn<<1.
Для собственной проводимости полупроводников и диэлектриков мы можем записать:
Полупроводники и диэлектрики отличаются шириной запрещенной зоны. В полупроводниках, как правило, запрещенная зона меньше
и не превышает 3 эВ, поэтому для полупроводников вероятность разрыва валентных связей за счет теплового нагрева значительно
больше, чем у диэлектриков и даже при комнатной температуре полупроводники могут обладать конечной электронной
проводимостью. При этом собственная концентрация носителей заряда от ширины запрещенной зоны и температуры. Уровень Ферми
в собственных полупроводниках и диэлектриках лежит в середине запрещенной зоны. В отличие от металлов в идеальных
собственных полупроводниках в середине зоны разрешенных уровней нет и соответственно не может быть электронов с такими
энергиями, однако если бы они были, то вероятность их заполнения была бы равна ½. Т.е. и в этом случае он указывает
на то какие состояния могут быть заполнены электронами, а какие нет. Действительно валентная зона ниже уровня Ферми - она
заполнена электронами, зона проводимости выше уровня Ферми, вероятность ее заполнения электронами fn<<1.
Для собственной проводимости полупроводников и диэлектриков мы можем записать:
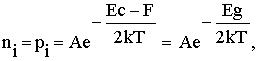 (13)
(13)
где А - величина слабо зависящая от температуры, Ec и F энергия дна зоны проводимости и уровня Ферми, Eg - ширина
запрещенной зоны, k - постоянная Больцмана, T - значение абсолютной температуры (К). Энергетическая диаграмма для
полупроводника, диэлектрика и металла на рис. 5 поясняет принятые энергетические обозначения.
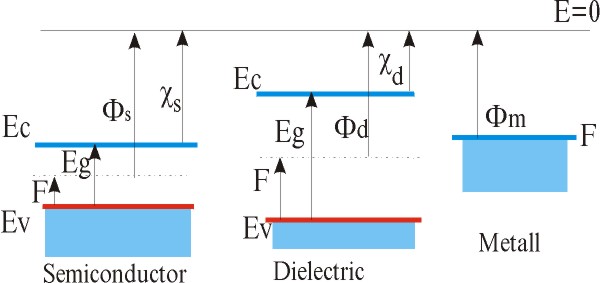
Рис. 5. Энергетические диаграммы полупроводника и диэлектрика.
 В дополнения к введенным обозначениям на рис. 5 через Фm обозначена работа выхода электрона из металла - это энергия,
которую необходимо сообщить электрону, чтобы он вышел в вакуум с нулевой кинетической энергией с уровня Ферми в металле
(соответствующий уровень энергии обозначен E=0). По аналогии были приняты понятия для работы выхода из полупроводника (Фs)
и диэлектрика (Фd), однако поскольку в этих матералах нет на уровне Ферми электронов и ее можно только рассчитать, то,
чтобы подчеркнуть это, такую работу выхода называют термодинамической. Измерить можно энергию, которую нужно сообщить
электрону, находящемуся в зоне проводимости, чтобы он вышел из кристалла. Эту энергию называют сродством к электрону, на
рис.5 она обозначена χs и χi.
В дополнения к введенным обозначениям на рис. 5 через Фm обозначена работа выхода электрона из металла - это энергия,
которую необходимо сообщить электрону, чтобы он вышел в вакуум с нулевой кинетической энергией с уровня Ферми в металле
(соответствующий уровень энергии обозначен E=0). По аналогии были приняты понятия для работы выхода из полупроводника (Фs)
и диэлектрика (Фd), однако поскольку в этих матералах нет на уровне Ферми электронов и ее можно только рассчитать, то,
чтобы подчеркнуть это, такую работу выхода называют термодинамической. Измерить можно энергию, которую нужно сообщить
электрону, находящемуся в зоне проводимости, чтобы он вышел из кристалла. Эту энергию называют сродством к электрону, на
рис.5 она обозначена χs и χi.
 Как видно из формулы собственная концентрация полупроводников (следовательно и проводимость) очень сильно зависят от
температуры. Концентрация, рассчитанная в соответствии с формулой 1 для диэлектриков дает значение близкое к 0
(в см-3).
Как видно из формулы собственная концентрация полупроводников (следовательно и проводимость) очень сильно зависят от
температуры. Концентрация, рассчитанная в соответствии с формулой 1 для диэлектриков дает значение близкое к 0
(в см-3).
 На рис. 6 показаны зависимости собственной концентрации от температуры для трех полупроводниковых материалов: германия,
кремния и арсенида галлия.
На рис. 6 показаны зависимости собственной концентрации от температуры для трех полупроводниковых материалов: германия,
кремния и арсенида галлия.
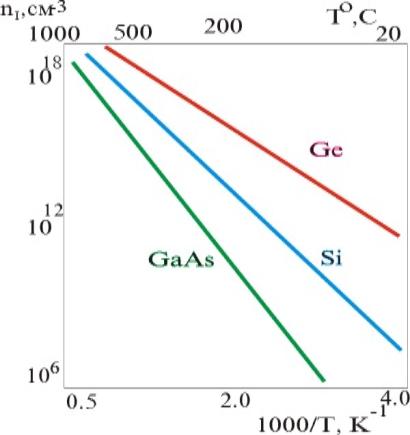
Рис. 6. Зависимость собственной концентрации электронов от обратной температуры в Ge, Si, GaAs.
 Свободные носители заряда, создающие электропроводность, движутся хаотически, сталкиваясь с атомами решетки и друг с другом.
Поскольку их поведение напоминает поведение частиц газа, для их описания используют основные понятия
молекулярно-кинетической теории газов, такие как: статистическую вероятность распределения электронов и дырок по энергиям,
понятие длины свободного пробега, диффузии частиц и другие . Такой подход является приближенным значительно упрощающим
реальные процессы в твердом теле, поэтому приходится вводить целый ряд поправок, которые с одной стороны усложняют модель,
с другой делают ее более соответствующей реальным процессам.
Свободные носители заряда, создающие электропроводность, движутся хаотически, сталкиваясь с атомами решетки и друг с другом.
Поскольку их поведение напоминает поведение частиц газа, для их описания используют основные понятия
молекулярно-кинетической теории газов, такие как: статистическую вероятность распределения электронов и дырок по энергиям,
понятие длины свободного пробега, диффузии частиц и другие . Такой подход является приближенным значительно упрощающим
реальные процессы в твердом теле, поэтому приходится вводить целый ряд поправок, которые с одной стороны усложняют модель,
с другой делают ее более соответствующей реальным процессам.
 Прежде всего все изменения характеристик свободных носителей заряда происходят на очень малых расстояниях, сравнимых с
расстояниями между атомами, составляющими несколько ангстрем, т.е. на расстояниях много меньших длины света. Следовательно
эти процессы должны подчиняться основным закономерностям, описываемым квантовой физикой. Согласно квантовой физике
энергия любых частиц микромира квантована.
Прежде всего все изменения характеристик свободных носителей заряда происходят на очень малых расстояниях, сравнимых с
расстояниями между атомами, составляющими несколько ангстрем, т.е. на расстояниях много меньших длины света. Следовательно
эти процессы должны подчиняться основным закономерностям, описываемым квантовой физикой. Согласно квантовой физике
энергия любых частиц микромира квантована.

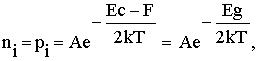 (13)
(13)

