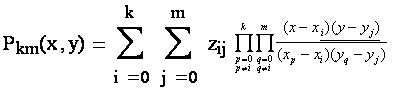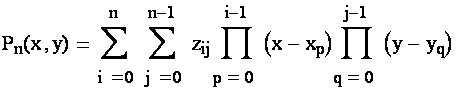8. Интерполирование функций.1) Необходимость: приблизить f(x) более простой функцией ф(х), совпадающей в узлах xi с f(xi), если f(x) определена только в узловых точках (результат эксперимента) или очень сложно вычисляется.
Условия Лагранжа : ф(х, с0, с1…сn) = fi, 0 < i < n, где сi - свободные параметры, определяемые из данной системы уравнений. С помощью интерполяции решают широкий круг задач численного анализа: дифференцирование и интегрирование функций, нахождение нулей и экстремумов, решение дифференцированных и т. д. Термин интерполяция употребляют, если х заключено между узлами, если он выходит за крайний узел, говорят об экстраполяции(при которой трудно гарантировать надежность приближения). 2) Пусть ф (х) = с0 + с1х + с2х2 +…+ сnxn (канонический вид полинома); сетка узлов может быть неравномерной. Коэффициенты сi определяю Получившаяся СЛАУ относительно свободных параметров сi имеет решение, если среди узлов
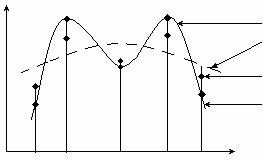
Общая блок-схема:
3) Пусть задано n+1 значение функции f(x) в узлах xj ф(х) = Pn(х) = Преимущества: потребуется решать СЛАУ для определения значения полинома в точке х. Недостатки: для каждого х полином требуется читать заново. Погрешность формулы: Увеличение числа узлов и, соответственно, степени полинома Pn(x) ведет к увеличению погрешности из-за роста производных 4) ф(х) = Pn(x) = A0+A1(x-x0)+A2(x-x0)(x-x1)+…+An(x-x0)(x-x1)…(x-xn-1) - многочлен Ньютона для n+1 узла. Коэффициенты Ф представляют собой разделенные разности и записываются в виде: А0 = f0 A1 = (f0-f1)/(x0-x1) = f01 A2 = (f01-f02)/(x1-x2) = f012, где f02 = (f0-f2)/(x0-x2) A3 = (f012-f013)/(x2-x3) = f0123 , где f013 = (f01-f03)/(x1-x3) , а f03 = (f0-f3)/(x0-x3) и в общем случае Ak = (f01…k-1-f01…k)/(xk-1-xk) Т.е. многочлен n-й степени выражается при помощи разделенных разностей через свои значения в узлах. Преимущества: не решается СЛАУ, однако вычисление коэффициентов полинома не зависит от значения х и может быть вычислено только один раз. При добавлении нового узла также не происходит пересчета коэффициентов, кроме последнего. После определения коэффициентов полинома Ньютона вычисление его значений при конкретных аргументах х наиболее экономично проводить по схеме Горнера: P2(x) = A0+ (x-x0)(A1+(x-x2)(A3+…)…)
Погрешность определяется тем же соотношением (*) Входящая в состав погрешности величина
! Между разделенными разностями и производными соответствующих порядков существует соотношение f <n>(x) ~ n! F01…n , где n – степень производной. Это используется в численном дифференцировании и при оценке погрешностей интерполяции. ! Можно строить полиномы, не только проходящие через заданные точки, но и имеющие в них заданные касательные (интерполяционный многочлен Эрмита) или заданную кривизну. Количество всех полагаемых условий должно быть n-1, если n – степень полинома. Основной недостаток интерполирования с помощью многочленов – неустранимые колебания, которые претерпевает кривая в промежутках между узлами. При этом повы Интерполяция сплайнами. Происхождение термина “сплайны” связано с гибкой чертежной линейкой, которой пользовались для рисования гладких кривых, проходящих через заданные точки. Из теории упругости следует, что получающаяся кривая имеет постоянную кривизну и разрывы возникают лишь в третьей производной. Обычно для сплайна выбирают кубический полином определенный на интервале х из [xi-1, хi]. При этом вся кривая представляет собой набор таких кубических полиномов, с определенным образом подобранными коэффициентами аi , bi , ci , di , i- параметр сплайна. ! Если вдоль сплайна совершается механическое движение, то непрерывность второй производной предполагает непрерывность ускорения и, следовательно, отсутствие резких изменений приложенной силы.
N+1 узлов N интервалов 4N неизвестных
Условия подбора коэффициентов: 1)условия Лагранжа: , 2)непрерывность первой и второй производной в узлах фi'(xi) = фi+ 3) условия в крайних узлах x0 и xn. Обычно задают условия свободных концов сплайна : ф1”(x0) = 0, фn”(xn) = 0 Из полученных условий определяются зависимости между коэффициентами сплайнов: В узле х = хi-1 коэффициент ai = fi-1. В следующем узле x = xi выполняется условие ai+bihi+cihi2+dihi3 = fi, где элементарный шаг hi = xi – xi-1. Потребуем непрерывности первой и второй производной на конце интервала фi/(x) = bi+2ci(x-xi-1)+3di(x-xi-1)2 , фi//(x) = 2ci+6di(x-xi-1); В узле x = xi первая производная фi/(xi) = bi+2cihi+3dihi2 (1) фi+1//(xi) = bi+1 (2) Приравнивая (1) и (2), получаем bi +2cihi+3dihi2 = bi+1. Вторая производная фi//(xi) = 2ci+6cihi (3) фi+1//(xi) = 2ci (4) Приравнивая (3) и (4), получаем в свою очередь ci+3dihi = ci+1. Таким образом стыкуем все полиномы в узлах 1 ≤ i ≤ n-1. В крайних точках диапазона ф1//(x0) = 2c1 = 0 → c1 = 0 ф1//(xn) = 2cn+6dnhn = 0 → cn +3dnhn = 0 Для всех 0 ≤ i ≤ n вышеприведенные соотношения представляют собой полную систему 4n линейных алгебраических уравнений относительно коэффициентов сплайнов, которую можно привести к системе ЛАУ, выразив коэффициенты ai, bi, di через ci и решить методом Гаусса или прогонки. Система N линейных уравнений для коэффициентов сi:
для где hi = xi-xi-1 После определения коэффициентов ci , 2N коэффициентов bi и di вычисляются по формулам:
И N уравнений для Сплайновая интерполяция хороша тем, что требует знания в узлах только значений функции, но не ее производных. Многомерная интерполяция 1) Последовательная интерполяция на прямоугольной сетке. Пусть заданы z i j = z(xi, yj) требуется найти z(x, y). Сначала при фиксированных yj0 найдем значение z(x, yj0), Затем по полученному набору значений найдем z(x, y). В случае интерполяции полиномом Лагранжа общая формула имеет вид
где k и m – количество узлов по сторонам прямоугольной сетки. 2) Треугольная конфигурация узлов. z (x0, x1, y) = [z(x0, y)-z(x1, y)]/(x0-x1) z (x, y0, y1) = [z(x, y0)-z(x,y1)]/(y0-y1) Многочлен Лагранжева типа в этом случае имеет вид
|
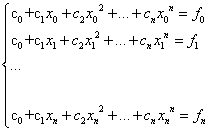тся из условий Лагранжа: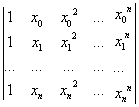
(
(*)
.
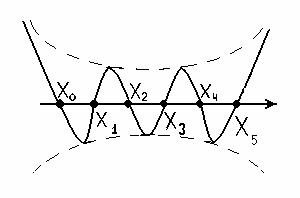
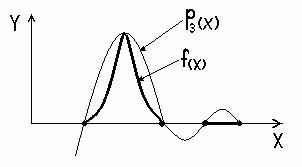(х-х
шение степени интерполяционного полинома для большинства решаемых уравнений приводит не к уменьшению, а к увеличению погрешности.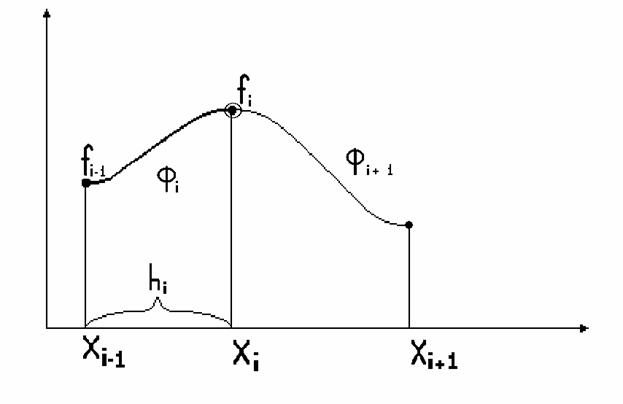 
, 
,
,
,
, 
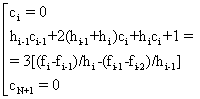
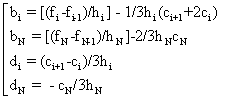