6. Численное дифференцирование
Методы численного дифференцирования применяются, если исходную функцию f(x) трудно или невозможно продифференцировать аналитически. Например, эта функция может быть задана таблично. Задача численного дифференцирования – выбрать легко вычисляемую функцию (обычно полином) 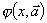 , для которой приближенно полагают
, для которой приближенно полагают 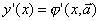 .
.
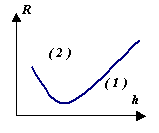
Численное дифференцирование – некорректная задача, так как отсутствует устойчивость решения. При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа. А так как значения функции обычно известны с определенной погрешностью, то все значащие цифры могут быть потеряны. На графике кривая (1) соответствует уменьшению погрешности дифференцирования при уменьшении шага; кривая (2) представляет собой неограниченно возрастающий (осциллирующий) вклад неустранимой погрешности исходных данных – значений функции y(x). Критерий выхода за оптимальный шаг при его уменьшении – «разболтка» решения: зависимость результатов вычислений становится нерегулярно зависящей от величины шага.
Пусть 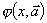 введена как интерполяционный многочлен Ньютона. В этом случае для произвольной неравномерной сетки:
введена как интерполяционный многочлен Ньютона. В этом случае для произвольной неравномерной сетки:
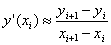 , для i = 0, 1…n-1, интерполяция полиномом первой степени.
, для i = 0, 1…n-1, интерполяция полиномом первой степени.
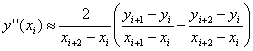 , интерполяция полиномом второй степени.
, интерполяция полиномом второй степени.
В общем случае 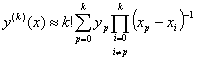 . Минимальное число узлов, необходимое для вычисления k-й производной, равно k+1.
. Минимальное число узлов, необходимое для вычисления k-й производной, равно k+1.
Оценка погрешности при численном дифференцировании может быть осуществлена по формуле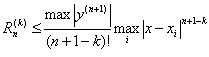 , где n – число узлов функции, k – порядок производной.
, где n – число узлов функции, k – порядок производной.
На практике чаще всего используются упрощенные формулы для равномерной сетки, при этом точность нередко повышается. Часто используются следующие формулы для трех узлов:
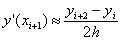 , где h = x1 – x0 = const.
, где h = x1 – x0 = const.
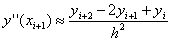 .
.
Исходя из общего вида интерполяционного полинома можно вывести формулы для более высокого порядка точности или для более высоких производных.

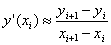 , для i = 0, 1…n-1, интерполяция полиномом первой степени.
, для i = 0, 1…n-1, интерполяция полиномом первой степени.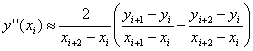 , интерполяция полиномом второй степени.
, интерполяция полиномом второй степени.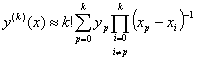 . Минимальное число узлов, необходимое для вычисления k-й производной, равно k+1.
. Минимальное число узлов, необходимое для вычисления k-й производной, равно k+1.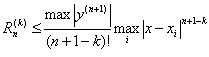 , где n – число узлов функции, k – порядок производной.
, где n – число узлов функции, k – порядок производной.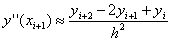 .
.