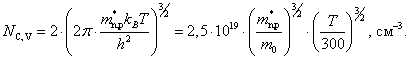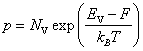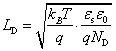РЕШЕНИЕ ЗАДАЧ
Глава 1. Принципы строения твердых тел. Элементы кристаллографии
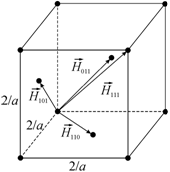
1.1. Нормаль
к плоскости (hkl) есть вектор ![]() обратной решетки [106]
обратной решетки [106]
|
|
(1.1.1) |
Угол между плоскостями равен углу между нормалями к ним
![]() ;
; ![]() .
.
Выразим
косинус угла между векторами ![]() (cosj)
через скалярное произведение векторов
(cosj)
через скалярное произведение векторов
![]() . Отсюда следует, что
. Отсюда следует, что
|
|
(1.1.2) |
Учтем, что
для ортогональных систем, которыми являются кристаллы кубической,
тетрагональной и ромбической сингоний, периоды обратной решетки можно
представить в виде: ![]() ;
; ![]() ;
; ![]() .
.
Примем ![]() ;
; ![]() ;
; ![]() как единичные вектора
нормалей к плоскостям (
как единичные вектора
нормалей к плоскостям (![]() ); (
); (![]() ). Тогда
). Тогда
![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() .
.
![]() ;
; ![]() .
.
1)
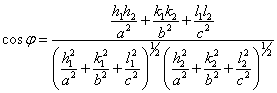
Общая запись cosj справедлива для случая ромбической сингонии,
где ![]() :
:
|
|
(1.1.3) |
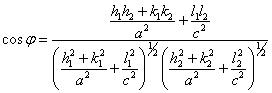
2)
Для тетрагональной сингонии ![]() , поэтому
, поэтому
|
|
(1.1.4) |
3)
Для кубической сингонии ![]()
|
|
(1.1.5) |
1.2.
Используем для решения задачи
понятие вектора обратной решетки ![]() .
.
![]() .
.
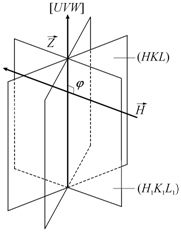
Вектор ![]() перпендикулярен оси
зоны, т. к. он перпендикулярен плоскости с индексами
перпендикулярен оси
зоны, т. к. он перпендикулярен плоскости с индексами![]() , а ось зоны лежит в этой плоскости (рис. 1.2.1).
, а ось зоны лежит в этой плоскости (рис. 1.2.1).
|
|
|
Рис. 1.2.1. Кристаллографическая зона, ось которой имеет индексы [UVW] |
Пусть ![]() – вектор оси зоны.
Тогда
– вектор оси зоны.
Тогда
|
|
(1.2.1) |
т. к. ![]() при
при ![]() .
.
Кроме того ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Тогда
|
|
(1.2.2) |
Следовательно, ![]() .
.
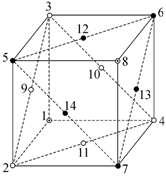
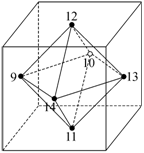
1.3. Рассмотрим послойное расположение атомов в ГЦК ячейке АВСАВСАВС… (рис. 1.3.1).
|
|
|
Рис. 1.3.1. Послойное расположение атомов в ГЦК ячейке |
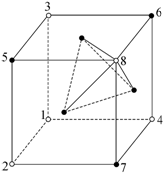
Узлы 12, 13, 14 третьего слоя и узел 8 четвертого слоя образуют между
собой тетраэдрическую пустоту (рис. 1.3.2), а узлы 9, 10, 11 второго слоя и 12,
13, 14 третьего слоя образуют октаэдрическую пустоту (рис. 1.3.3).
|
|
|
|
Рис. 1.3.2. Тетраэдрическая пустота |
Рис. 1.3.3. Октаэдрическая пустота |
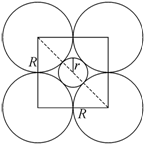
а) Рассмотрим октаэдрическую пустоту.
Для этого построим сечение шаров плоскостью, проходящей через узлы 9,
10, 14, 13 (рис. 1.3.4).
|
|
|
Рис. 1.3.4. Сечение ГЦК ячейки |
Если R -
радиус атомов, образующих ГЦК ячейку, а r -
радиус внедренного в октаэдрическую пустоту атома, то переходя к периоду
ячейки, из простых геометрических соображений получим ![]() . Из приведенного рисунка
. Из приведенного рисунка ![]() , поэтому
, поэтому ![]() . Следовательно радиус внедренного в октопустоту атома не может
превышать
. Следовательно радиус внедренного в октопустоту атома не может
превышать ![]()
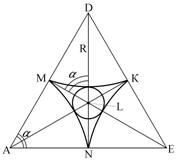
б) Рассмотрим тетраэдрическую пустоту.
бозначим ABCD – правильный тетраэдр, сложенный атомами 8, 12,13, 14. Ребро тетраэдра имеет длину, равную 2R.
Построим сечение тетраэдра плоскостью ADE, перпендикулярной ребру ВС (рис. 1.3.5).
|
|
|
Рис. 1.3.5. Сечение тетраэдра, сложенного атомами 8, 12,13, 14 |
Высота DN перпендикулярна АE, а AK перпендикулярна DE.
![]() .
. ![]() .
. ![]() .
.
![]() .
.
![]() .
.
![]() .
. ![]() .
.![]() .
.
![]() .
.
Отсюда следует, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В
тетраэдрическую пустоту поместится атом радиусом 0,22R. Значит ![]() и
и ![]()
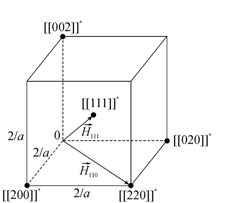
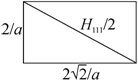
1.4. а) Рассмотрим ГЦК решетку (рис. 1.4.1).
|
|
|
Рис. 1.4.1. |
Ближайшие
к началу координат плоскости семейств ![]() ,
, ![]() и
и ![]() находятся от него на
расстоянии
находятся от него на
расстоянии ![]() , значит соответствующие межплоскостные расстояния
, значит соответствующие межплоскостные расстояния ![]() . Отсюда следует, что периоды обратной решетки
. Отсюда следует, что периоды обратной решетки ![]() .
.
Для плоскостей ![]() рассчитаем
межплоскостное расстояние (для h, k, l различной четности: 2h, 2k, 2l)
рассчитаем
межплоскостное расстояние (для h, k, l различной четности: 2h, 2k, 2l) ![]() .
.
Вектор ![]() перпендикулярен плоскости
(110), т. е. лежит в нижней грани обратной ячейки по ее диагонали (рис. 1.4.2).
перпендикулярен плоскости
(110), т. е. лежит в нижней грани обратной ячейки по ее диагонали (рис. 1.4.2).
|
|
|
Рис. 1.4.2. |
![]()
Для
семейства плоскостей ![]()
![]() . Следовательно,
. Следовательно, ![]() .
.
|
|
Подсчитаем длину пространственной диагонали обратной решетки
|
Значит,
конец вектора ![]() лежит на середине
пространственной диагонали, т. е. в центре куба. Следовательно, прямой ГЦК
решетке соответствует обратная ОЦК.
лежит на середине
пространственной диагонали, т. е. в центре куба. Следовательно, прямой ГЦК
решетке соответствует обратная ОЦК.
б) Рассмотрим ОЦК решетку (рис. 1.4.3).
|
|
|
Рис. 1.4.3. |
Модули
периодов обратной решетки ![]() ,
, ![]() и
и ![]() вновь получаем равными
вновь получаем равными
![]() , поскольку ближайшие к началу координат плоскости (
, поскольку ближайшие к началу координат плоскости (![]() ,
, ![]() и
и ![]() ) опять проходят через центр куба.
) опять проходят через центр куба.
Межплоскостное расстояние ![]() равно половине
диагонали квадрата, или (по правилу для ОЦК, если
равно половине
диагонали квадрата, или (по правилу для ОЦК, если ![]() – четное число)
– четное число) ![]() , т. е.
, т. е. ![]() . Длина диагонали грани обратной решетки равна
. Длина диагонали грани обратной решетки равна ![]() . Значит, конец вектора
. Значит, конец вектора ![]() находится в середине
нижней грани (рис. 1.4.4).
находится в середине
нижней грани (рис. 1.4.4).
|
|
|
Рис. 1.4.4. |
Для семейств плоскостей ![]() и
и ![]() можно сделать
аналогичные выводы.
можно сделать
аналогичные выводы.
Рассмотрим плоскость ![]() . Межплоскостное расстояние
. Межплоскостное расстояние ![]() .
. ![]() – это длина
пространственной диагонали куба.
– это длина
пространственной диагонали куба.
Следовательно, ОЦК прямой решетки соответствует ГЦК обратная. Трансляцией получают остальные узлы обратной решетки для прямой ОЦК решетки.
Глава 2. Природа и типы межатомных связей
2.1.
Запишем формулу энергии связи ионов![]() :
:
|
|
(2.1.1) |
Условие равновесного расстояния R0 между ионами – это равенство 0 производной по R
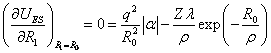 .
.
Отсюда следует,
что ![]() .
.
Для
ионного соединения NaCl
характерны заряды ионов Na1+Cl1-. Значит, до
изменения заряд ионов был ![]() . Таким образом
. Таким образом
|
|
(2.1.2) |
Когда
заряд изменился в 2 раза, ![]() , отсюда
, отсюда
|
|
(2.1.3) |
Для того
чтобы определить, как изменится равновесное расстояние![]() , найдем отношение формулы (2.1.3) к формуле (2.1.2)
, найдем отношение формулы (2.1.3) к формуле (2.1.2)
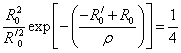 .
.
Отсюда 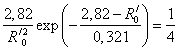 .
.
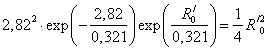 →
→ ![]() ,
,
![]() .
.
Используя
методы решения нелинейных уравнений, находим![]() .
.
Полную энергию решетки, состоящей из 2N ионов, находящихся в состоянии равновесия, можно записать как
|
|
(2.1.4) |
Подставляя
в формулу (2.1.4) численные значения величин, ![]() .
.
![]() , находим отношение энергий связи
, находим отношение энергий связи ![]() .
.
При возрастании q в 2 раза равновесное расстояние уменьшается примерно до 2,22 Å, а энергия уменьшается приблизительно в 5 раз.
2.2.
Для одномерной цепочки ![]() ;
; ![]() ;
; ![]() . Это равенство подобно тому, если разложить в ряд Тейлора
. Это равенство подобно тому, если разложить в ряд Тейлора ![]() .
.
![]() .
.
При ![]()
![]() и сходится к значению,
стоящему в скобках для α.
Значит, постоянная Маделунга
и сходится к значению,
стоящему в скобках для α.
Значит, постоянная Маделунга![]() .
.
2.3. Потенциал притяжения вандерваальсовой связи описывается выражением
|
|
(2.3.1) |
По условию
задачи ![]() .
.
Если
потенциал отталкивания ![]() , то
, то 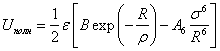 .
.
![]() , т. е.
, т. е. ![]() .
.
![]() . В этом выражении неизвестно В. Найдем его из условия
. В этом выражении неизвестно В. Найдем его из условия ![]() в равновесном
состоянии
в равновесном
состоянии
![]() .
.
Из этого
следует ![]() . Следовательно,
. Следовательно, ![]() или
или ![]() , т. е.
, т. е. ![]() .
.
Характеристическая длина потенциала отталкивания составляет
приблизительно 0,033 Å
2.4.
Для ионных кристаллов вид зависимости потенциала отталкивания от
межатомного расстояния достаточно точно описывается соотношением ![]() (λ и β –
постоянные величины, получаемые из экспериментов).
(λ и β –
постоянные величины, получаемые из экспериментов).
Если ![]() существен только для
ближайших соседей, то для энергии кристалла типа NaCl получим
существен только для
ближайших соседей, то для энергии кристалла типа NaCl получим 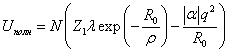 , где
, где ![]() – число ближайших
соседей.
– число ближайших
соседей.
В равновесии 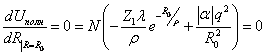 . Отсюда
. Отсюда ![]() .
.
![]() .
.
Подставим выражение в ![]()
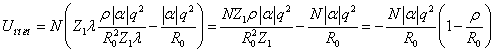 .
.
![]() определяется из
эксперимента, и в задаче он приведен.
определяется из
эксперимента, и в задаче он приведен.
Для
определения характеристической длины потенциала отталкивания используют тот
факт, что полная энергия связана с модулем всестороннего сжатия В следующим образом:![]() .
.
В структуре KCl расстояние между соседними ионами
равно половине периода ячейки, т. е. ![]() .
.
В элементарной ячейке
содержатся 4 молекулы KCl,
т. е. ![]() .
.
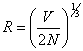 .
.
 ;
;  .
.
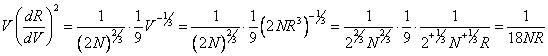 .
.
![]() найдем из общего
выражения для полной энергии
найдем из общего
выражения для полной энергии
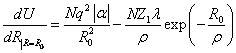 .
.
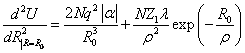 .
.
![]() .
.
![]() .
.
В системе СГС
Заряд ![]() СГСЕ.
СГСЕ.
![]() .
.
![]() .
.
![]() ;
; ![]() ;
; 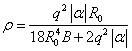 .
.
![]() .
.
![]() .
.
![]() .
.
В равновесном состоянии
энергия связи (в системе СИ) 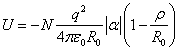 .
.
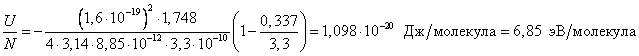
![]() .
.
Следовательно, характеристическая
длина потенциала отталкивания составляет примерно 0,337 Å, а энергию
связи по отношению к энергии ионов, разведенных на бесконечное расстояние - ![]() .
.
Глава 3. Дефекты и диффузия в твердых телах
3.1.
а) Пусть U – энергия, необходимая для
образования дефектов Шоттки, n – число вакантных узлов
решетки, а N – число узлов решетки, занятых
атомами. Тогда суммарная энергия, необходимая для образования n дефектов, равна ![]() . Энтропия системы
. Энтропия системы ![]() , причем вероятность w
определяется как
, причем вероятность w
определяется как ![]() . Отсюда следует, что если воспользоваться приближением
Стирлинга (
. Отсюда следует, что если воспользоваться приближением
Стирлинга (![]() ), то свободная энергия при температуре Т К получится
равной
), то свободная энергия при температуре Т К получится
равной
![]() .
.
При равновесии
![]() ,
,
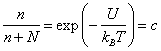 ,
,
где с – концентрация дефектов в расчете на число атомных узлов.
Для
металлов обычно ![]() эВ, так что
равновесная концентрация вакансий при комнатной температуре получается порядка
10-5. Если
эВ, так что
равновесная концентрация вакансий при комнатной температуре получается порядка
10-5. Если ![]() , то число дефектов будет
, то число дефектов будет
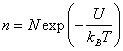 .
.
б) Пусть U – энергия, необходимая, чтобы внедрить один атом, N – общее число узлов решетки, N /
– число возможных межузельных положений, а n – число межузельных
положений, занятых атомами. Вероятность w
равна 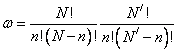 . Подставляя значение w
в выражение для свободной энергии, получаем, что при равновесии
. Подставляя значение w
в выражение для свободной энергии, получаем, что при равновесии
 ,
,
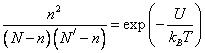 ,
,
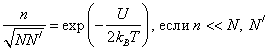 .
.
Для
кубического кристалла ![]() , поэтому равновесная концентрация дефектов Френкеля при
температуре Т оказывается равной
, поэтому равновесная концентрация дефектов Френкеля при
температуре Т оказывается равной 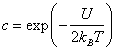 .
.
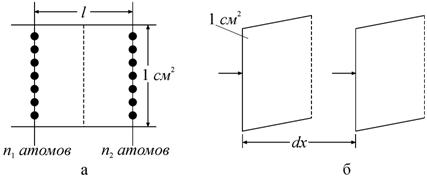
3.2. Рассмотрим две параллельные единичные площадки из межузельных атомов, находящиеся на расстоянии l друг от друга (рис. 3.2.1, а).
|
|
|
Рис. 3.2.1. Модели, по которым выводятся законы Фика для диффузии межузельных атомов |
Пусть соответствующие числа занятых узлов равны n1 и n2. Один атом совершает f скачков в секунду. Поэтому N атомов совершают Nf скачков в секунду, т. е. в целом, если N – общее число атомов, то в секунду происходит Nf скачков. Отсюда
![]() .
.
Поток
диффундирующих через площадку АВ атомов равен ![]() (множитель 1/2 введен
потому, что половина атомных скачков происходит в одном направлении, а вторая
половина – в противоположном).
(множитель 1/2 введен
потому, что половина атомных скачков происходит в одном направлении, а вторая
половина – в противоположном).
Объемная
концентрация межузельных атомов ![]() , и если
, и если ![]() , то
, то ![]() ,
, ![]() . Отсюда получим
. Отсюда получим ![]() , где
, где ![]() – коэффициент
диффузии.
– коэффициент
диффузии.
Рассмотрим теперь единичную площадку на расстоянии dx (рис. 3.2.1, б):
![]() .
.
Изменение
концентрации во времени ![]() .
.
Для
перескока межузельного атома из одного положения в соседнее нужно сообщить ему
дополнительную энергию, чтобы он смог «втиснуться» между мешающими ему атомами
матрицы. Допустим, что этот процесс представляет собой случайное блуждание.
Можно полагать, что частота его будет выражаться так: 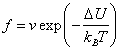 , где v – постоянная, DU – потенциальный барьер между соседними межузельными
положениями, Т – абсолютная
температура, kB – постоянная Больцмана.
, где v – постоянная, DU – потенциальный барьер между соседними межузельными
положениями, Т – абсолютная
температура, kB – постоянная Больцмана.
Поскольку необходимо, чтобы рядом с занятым междоузлием было незанятое, предположение о случайных блужданиях годится только для диффузии межузельных атомов в очень разбавленных растворах. Это предположение недопустимо в случае диффузии атомов замещения, где весьма существенны эффекты корреляции. Разберем пример такого эффекта.
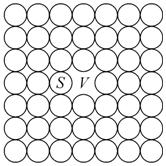
Пусть (рис. 3.2.2) атом замещения S перескакивает в вакантный узел V. Но если не уйдет новая вакансия или не подойдет другая вакансия, весьма вероятно, что S и V снова обменяются местами, т. е. диффузия не будет процессом случайного блуждания.
|
|
|
Рис. 3.2.2. Корреляционные эффекты при самодиффузии |
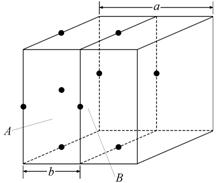
3.3. а) Кристаллическая структура налагает геометрические ограничения на коэффициент диффузии. Как пример рассмотрим диффузию внедренных атомов в ОЦК структуре.
На рис.
3.3.1. показаны две смежные плоскости (А
и В) из межузельных атомов в
элементарной ОЦК ячейке. На плоскости А
имеется один (4/4) межузельный атом, который может перескочить на плоскость В. Из каждых двух межузельных атомов
один не может перескакивать, потому что на пути находится атом в центре объема
ячейки. Поэтому из 1,5 межузельного атома на плоскости А только 2/3 могут перескакивать на плоскость В. Таким образом, эффективная частота скачков равна ![]() . Длина перескока
. Длина перескока ![]() , где а – параметр
решетки. Поэтому коэффициент диффузии для межузельной диффузии в ОЦК кристалле
будет равен
, где а – параметр
решетки. Поэтому коэффициент диффузии для межузельной диффузии в ОЦК кристалле
будет равен
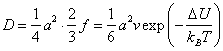 .
.
|
|
|
Рис. 3.3.1. Межузельные положения в элементарной ОЦК ячейке |
б)
Температурная зависимость очевидна из классической статистико-механической
трактовки частоты скачков. Дальнейшие термодинамические ограничения
коэффициента диффузии обусловлены тем, что потенциальное поле ![]() , в котором движется межузельный атом, является полем
колебательным, поэтому
, в котором движется межузельный атом, является полем
колебательным, поэтому ![]() нужно заменить полем
нужно заменить полем ![]() , где X – координаты всех атомов, кроме
атома, находящегося в точке
, где X – координаты всех атомов, кроме
атома, находящегося в точке ![]() , а Р – их моменты.
Следовательно, DU нужно заменить изменением свободной энергии DG, необходимым, чтобы медленно двигать диффундирующий
межузельный атом от дна к вершине потенциального барьера. (Величина DG называется свободной энергией активации.) Тогда коэффициент
диффузии для межузельной диффузии, например в ОЦК кристалле, можно записать
так:
, а Р – их моменты.
Следовательно, DU нужно заменить изменением свободной энергии DG, необходимым, чтобы медленно двигать диффундирующий
межузельный атом от дна к вершине потенциального барьера. (Величина DG называется свободной энергией активации.) Тогда коэффициент
диффузии для межузельной диффузии, например в ОЦК кристалле, можно записать
так:
|
|
(3.3.1) |
где
величина DG на основании уравнения Гиббса–Гельмгольца равна ![]() . Считая DН и DТ не зависящими от температуры, получаем
. Считая DН и DТ не зависящими от температуры, получаем
|
|
(3.3.2) |
(Заметим, что наклон кривой ![]() равен DН, а не DG.)
равен DН, а не DG.)
Обычно записывают:
|
|
(3.3.3) |
где ![]() . Экспериментально получено, что
. Экспериментально получено, что ![]() . Эта аномалия обусловлена энтропийным фактором
. Эта аномалия обусловлена энтропийным фактором 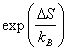 , который можно оценить следующим образом.
, который можно оценить следующим образом.
Рассмотрим
модель, построенную на основании теории упругости: ![]() , где m
–- модуль сдвига. Имеем
, где m
–- модуль сдвига. Имеем
|
|
(3.3.4) |
|
|
(3.3.5) |
т. е. ![]() определяется скоростью
изменения модуля сдвига при изменении температуры. Подставляя
определяется скоростью
изменения модуля сдвига при изменении температуры. Подставляя ![]() ,
, ![]() эВ, получаем
эВ, получаем
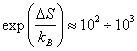 ,
,
где ![]() .
.
в) Рассмотрим кристалл, к которому приложено чисто сдвиговое напряжение (рис. 3.3.2).
Приложенное
напряжение может совершать работу, рождая вакансии на растянутых гранях и
перенося их к сжатым граням. Пусть U – энергия образования
вакансий. В присутствии приложенного напряжения сдвига ![]() эта энергия
уменьшается до
эта энергия
уменьшается до ![]() , если считать, что
, если считать, что ![]() – площадь,
приходящаяся на один атом, на которую действует нормальное напряжение, а
– площадь,
приходящаяся на один атом, на которую действует нормальное напряжение, а ![]() – работа, которую надо
затратить, чтобы удалить этот атом.
– работа, которую надо
затратить, чтобы удалить этот атом.
|
|
|
Рис. 3.3.2. Миграция точечных дефектов под действием напряжения |
Таким
образом, при тепловом равновесии концентрация вакансий на растянутых гранях
больше, чем на сжатых, на величину 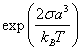 , т. е. эффект приложенного напряжения заключается в том, что
изменяется градиент концентраций вакансий.
, т. е. эффект приложенного напряжения заключается в том, что
изменяется градиент концентраций вакансий.
Считая,
что к результирующей диффузии вакансий можно применять законы Фика, получаем,
что поток атомов равен ![]() , где l – длина образца, D – коэффициент диффузии, а
, где l – длина образца, D – коэффициент диффузии, а ![]() .
.
Прирост
деформации, обусловленный каждой перенесенной вакансией, равен ![]() , поэтому скорость деформации оказывается равной
, поэтому скорость деформации оказывается равной ![]() .
.
3.4. Эту задачу впервые решали Гринвуд и Спейт для случая миграции газовых пузырьков продуктов расщепления в ядерном горючем.
Рассмотрим
сферическую пору с диаметром, равным целому числу межатомных расстояний na. Объем такой поры, равный ![]() , в
, в ![]() раз больше объема
атома матрицы. Поэтому, если атом с поверхности перескакивает на расстояние а, то пузырек газа перескакивает на
расстояние
раз больше объема
атома матрицы. Поэтому, если атом с поверхности перескакивает на расстояние а, то пузырек газа перескакивает на
расстояние ![]() . Кроме того, т. к. на поверхности пузырька имеется
. Кроме того, т. к. на поверхности пузырька имеется ![]() атомов, частота
скачков пузырька равна
атомов, частота
скачков пузырька равна ![]() , если f – частота скачка для
атома, диффундирующего сквозь поверхность пузырька. Считая движение такой поры
аналогичным броуновскому движению, приходим к выводу, что коэффициент диффузии D пропорционален произведению частоты скачка на квадрат длины
скачка, т. е.
, если f – частота скачка для
атома, диффундирующего сквозь поверхность пузырька. Считая движение такой поры
аналогичным броуновскому движению, приходим к выводу, что коэффициент диффузии D пропорционален произведению частоты скачка на квадрат длины
скачка, т. е.
|
|
(3.4.1) |
Если
считать, что вид f такой же, как в задаче 3.2,
то эту формулу можно переписать так: 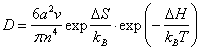 , где v – дебаевская частота, kB – постоянная Больцмана, Т – абсолютная температура, а DS и DH – соответственно изменения энтропии и энтальпии при
изменении свободной энергии DG, необходимом для того, чтобы
продвинуть диффундирующий атом сквозь энергетический барьер между соседними
узлами решетки.
, где v – дебаевская частота, kB – постоянная Больцмана, Т – абсолютная температура, а DS и DH – соответственно изменения энтропии и энтальпии при
изменении свободной энергии DG, необходимом для того, чтобы
продвинуть диффундирующий атом сквозь энергетический барьер между соседними
узлами решетки.
Поскольку длина скачка обратно пропорциональна n3, а частота его прямо пропорциональна n2, то очевидно, что миграция поры в результате поверхностной диффузии должна происходить со скоростью, обратно пропорциональной n. Иначе говоря, скорость миграции обратно пропорциональна радиусу поры.
Глава 4. Механические свойства твердых тел
4.2
Пусть ![]() − векторы,
соединяющие 5-й атом с n-м атомом соответственно в
недеформированном и деформированном состоянии. Тогда, например,
− векторы,
соединяющие 5-й атом с n-м атомом соответственно в
недеформированном и деформированном состоянии. Тогда, например,
![]() ,
,
где ![]() − векторы,
определяющие (кубическую) элементарную ячейку в начальном состоянии, а
− векторы,
определяющие (кубическую) элементарную ячейку в начальном состоянии, а ![]() − те же векторы
после деформации. Тогда
− те же векторы
после деформации. Тогда
![]()
Из свойств детерминантов и
определения ![]() можно найти, что при заданной деформации
можно найти, что при заданной деформации
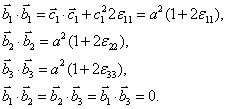
Следовательно,
в деформированном состоянии элементарная ячейка будет прямоугольным
параллелепипедом. Длина ![]() , например, находится из выражения для скалярного
произведения
, например, находится из выражения для скалярного
произведения ![]() с самим собой:
с самим собой:
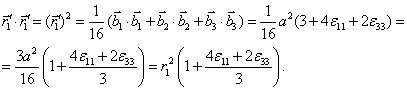
Аналогично
![]() ,
,
и, следовательно, для заданной деформации длины всех связей равны друг другу.
Пусть ![]() − углы между
связью, соединяющей 5-й атом с m-м атомом, и связью,
соединяющей 5-й атом с n-м атомом в недеформированной и деформированной
конфигурациях соответственно. Тогда можно записать
− углы между
связью, соединяющей 5-й атом с m-м атомом, и связью,
соединяющей 5-й атом с n-м атомом в недеформированной и деформированной
конфигурациях соответственно. Тогда можно записать
![]()
Из первой
части следует, что ![]() , т. е.
, т. е. ![]() и
и
![]()
Для
недеформированного состояния ![]() .
.
Аналогично
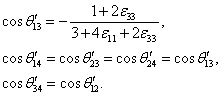
Таким образом, углы между связями, одинаковые в недеформированном кристалле, после деформации не будут одинаковыми.
4.2 Уравнения движения малого элемента объема под действием упругих сил имеют вид
![]()
где ![]() − компоненты
тензора напряжений. Для малых перемещений, рассматриваемых в задаче,
− компоненты
тензора напряжений. Для малых перемещений, рассматриваемых в задаче,

Компоненты
тензора напряжений ![]() связаны с компонентами
перемещений следующим соотношением:
связаны с компонентами
перемещений следующим соотношением:
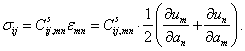
Отсюда
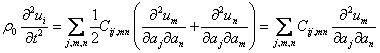
(т. к. ![]() )
)
а) Применим решения этих уравнений для плоских волн, распространяющихся вдоль направления [100]. Эти волны вызовут смещения, определяемые из уравнения
![]() ,
,
где ![]() − циклическая
частота,
− циклическая
частота, ![]() − волновой
вектор. Вектор
− волновой
вектор. Вектор ![]() направлен по нормали к
фронту волны и в этом случае может быть записан как
направлен по нормали к
фронту волны и в этом случае может быть записан как ![]() , где
, где ![]() − единичный
вектор в направлении оси 1. Поскольку
− единичный
вектор в направлении оси 1. Поскольку ![]() , то
, то
![]()
Отсюда
следует, что из всех производных от компонент вектора ![]() отличны от нуля только
производные по
отличны от нуля только
производные по ![]() . Таким образом, уравнения принимают вид
. Таким образом, уравнения принимают вид
![]()
или
![]()
Учет
ограничений, налагаемых на компоненты постоянной упругой жесткости ![]() кубической симметрией,
дает
кубической симметрией,
дает
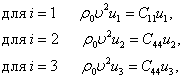
где ![]() − скорость
распространения волны.
− скорость
распространения волны.
Решениями этих уравнений будут
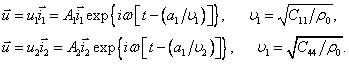
Из-за
идентичности уравнений для ![]() любое перемещение вида
любое перемещение вида
![]() удовлетворяет этим
уравнениям. Эти смещения поперечны по отношению к направлению распространения
волны. Решение для
удовлетворяет этим
уравнениям. Эти смещения поперечны по отношению к направлению распространения
волны. Решение для ![]() соответствует
продольной волне.
соответствует
продольной волне.
б) Для случая распространения вдоль направления [110] решение имеет вид
![]() ,
,
где ![]() , т. е.
, т. е.
![]()
Из всех
производных от компонент ![]() отличны от нуля только
производные по
отличны от нуля только
производные по ![]() . Таким образом, уравнения примут вид
. Таким образом, уравнения примут вид
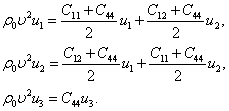
Третье из них дает нам решение
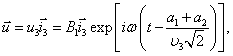
где ![]() − скорость
поперечной волны, поляризованной в направлении [001].
− скорость
поперечной волны, поляризованной в направлении [001].
Первые два уравнения решить непосредственно нельзя, но если решать их совместно, то, очевидно, придем к двум решениям (4.2.1) и (4.2.2):
|
|
(4.2.1) |
Здесь 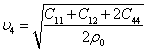 .
.
Это решение определяет волну, у которой все смещения направлены вдоль [110], т. е. волна продольная.
|
|
(4.2.2) |
где 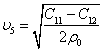 .
.
Следовательно,
все смещения направлены вдоль ![]() , т. е. это волна поперечная.
, т. е. это волна поперечная.
Глава 5. Динамика кристаллической решетки
5.1. Среднеквадратичные смещения атома при тепловых колебаниях можно найти, сопоставляя классические и квантовые значения энергии гармонического осциллятора.
|
|
(5.1.1) |
![]() .
.
Поскольку
средняя энергия, возбужденная гармоническим осциллятором под нулевым уровнем,
равна ![]()
![]() , то
, то ![]() ,
, 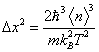 .
.
5.2. В линейной двухатомной цепочке возникают две ветви колебаний квадраты частот которых
|
|
(5.2.1) |
Групповая скорость волн

При ![]() , т. е. на границе зоны Бриллюэна
, т. е. на границе зоны Бриллюэна ![]() .
.
При ![]() , т. е. в центре зоны Бриллюэна
, т. е. в центре зоны Бриллюэна ![]() , поэтому
, поэтому
|
|
(5.2.2) |
Преобразуем выражение под корнем в формуле (5.2.2) к виду
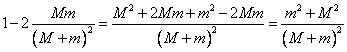 .
.
Тогда групповая скорость для двух волн, распространяющихся в цепочке, будет иметь вид
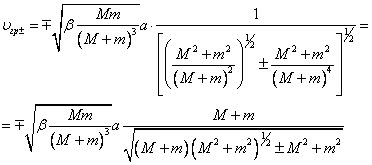
5.3. В модели Дебая ![]() ;
; ![]() , т. е. на объем
, т. е. на объем ![]() приходится 1 значение
волнового вектора
приходится 1 значение
волнового вектора ![]() . Число N состояний в объеме
сферы
. Число N состояний в объеме
сферы ![]() , будет равно
, будет равно ![]() ; в модели Дебая циклическая частота колебаний
; в модели Дебая циклическая частота колебаний ![]() , т. е.
, т. е. ![]() . Характеристическая частота колебаний Дебая
. Характеристическая частота колебаний Дебая ![]() определяется из
условия нормировки
определяется из
условия нормировки 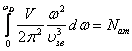 .
.
![]() .
. ![]() .
. 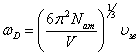 . Волновой вектор
. Волновой вектор ![]() , соответствующий частоте
, соответствующий частоте ![]() можно определить из соотношения
можно определить из соотношения 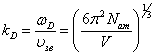 .
.
Число
атомов в единице объема ![]() можно найти как отношение числа атомов, приходящихся на
элементарную ячейку, к объему элементарной ячейки. В алмазе на кубическую
ячейку приходится 8 атомов, объем ячейки
можно найти как отношение числа атомов, приходящихся на
элементарную ячейку, к объему элементарной ячейки. В алмазе на кубическую
ячейку приходится 8 атомов, объем ячейки
![]() . Кратчайшее межатомное расстояние
. Кратчайшее межатомное расстояние ![]() – это расстояние от
узла, находящегося в начале координат, до узла в начале второй ГЦК ячейки с
координатами
– это расстояние от
узла, находящегося в начале координат, до узла в начале второй ГЦК ячейки с
координатами ![]() . Расстояние r связано с периодом
ячейки а соотношением
. Расстояние r связано с периодом
ячейки а соотношением ![]() , т. е.
, т. е. ![]() . Отсюда
. Отсюда ![]() . Следовательно, скорость звука в алмазе
. Следовательно, скорость звука в алмазе![]() .
.
Глава 6. Тепловые свойства твердых тел
6.1. В одномерной цепочке распространяется только продольная волна. Закон дисперсии
|
|
(6.1.1) |
Частота достигает
максимального значения ![]() .
.
Плотность
состояний ![]() .
.
При малых
волновых числах k частота![]() .
.
Энергия
волны, распространяющейся в цепочке и имеющей частоту w:
![]() .
.
Число волн, возникающих в цепочке, равно числу атомов в цепочке N.
Вероятность
существования волны с частотой w,
т. е. с энергией ![]() ,
, 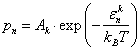 , т. е.
, т. е. 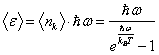 – то же значение, что
и для трехмерной решетки.
– то же значение, что
и для трехмерной решетки.
Тепловая
энергия системы ![]() . В приближении Эйнштейна все частоты одинаковы и равны
. В приближении Эйнштейна все частоты одинаковы и равны ![]() , т. е.
, т. е. ![]() – d-функция
и
– d-функция
и 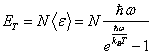 . Отсюда теплоемкость решетки при постоянном объеме в
приближении Эйнштейна выражается соотношением
. Отсюда теплоемкость решетки при постоянном объеме в
приближении Эйнштейна выражается соотношением
|
|
(6.1.2) |
При ![]() , т. е. при низких температурах,
, т. е. при низких температурах, 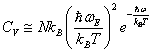 .
.
В модели Дебая:
1)
нет дисперсии, т. е. ![]() ;
;
2)
разрешенное значение ![]() , где
, где ![]() ;
;
3)
![]() ;
; ![]() ;
; ![]() .
.
Число
разрешенных значений волнового числа k – одно на длину ![]() , т. е. плотность на единицу длины цепочки равна
, т. е. плотность на единицу длины цепочки равна ![]() .
.
Таким
образом, на длину, равную k, в k-пространстве
приходится число разрешенных значений ![]() .
. ![]() – есть постоянная
величина, не зависящая от частоты.
– есть постоянная
величина, не зависящая от частоты.
1)
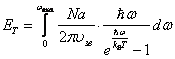 . Обозначим
. Обозначим![]() ;
; ![]() ;
; ![]() ;
; ![]() . Тогда
. Тогда 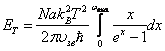
![]() найдем из условия нормировки
найдем из условия нормировки 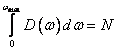 .
.
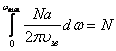 ;
; ![]() ;
; ![]() , таким образом,
, таким образом, 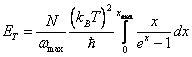 ;
; ![]() .
.
2)
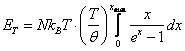 .
.
Из первого
пункта  .
.
Опять перейдем к обозначениям: ![]() ;
; ![]() ;
; ![]() .
.
3)
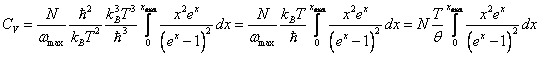 .
.
При ![]() , т.
е. при низких температурах, верхний предел интегрирования можно продлить до
бесконечности, тогда из пункта 2) получим
, т.
е. при низких температурах, верхний предел интегрирования можно продлить до
бесконечности, тогда из пункта 2) получим ![]() . Следовательно
. Следовательно ![]() .
. ![]()
6.2. По теории Дебая 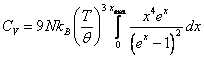 . При высоких температурах
. При высоких температурах ![]() и
и ![]() ,
тогда
,
тогда
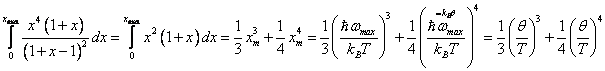 .
.
![]() и стремится к
и стремится к ![]() при
при ![]() .
.
6.3. ![]() ;
; ![]() ;
; ![]() ; Атомный вес
; Атомный вес ![]() а.е.м. Необходимо найти b.
а.е.м. Необходимо найти b.
В теории
Дебая ![]() частота линейно зависит от k;
частота линейно зависит от k; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() .
.
1 ![]() .
.
В модели
Эйнштейна ![]() собственная частота
колебаний – постоянная величина и находится из уравнения движения частицы,
совершающей колебания вдоль оси x:
собственная частота
колебаний – постоянная величина и находится из уравнения движения частицы,
совершающей колебания вдоль оси x: ![]() или
или ![]() .
.
Собственная
частота колебания частиц ![]() , тогда
, тогда ![]() .
.
![]() .
.
6.4. Хорошим приближением для
описания колебательных свойств твердых тел служит модель Дебая. В ней принято,
что число частот, заключающихся в промежутке от v до ![]() , пропорционально
, пропорционально ![]() . Поэтому распределение частот может быть записано в виде
. Поэтому распределение частот может быть записано в виде
|
|
(6.4.1) |
что в сумме дает
|
|
(6.4.2) |
где N – число всех атомов.
Если распределение (6.4.1) подставить в выражение для теплоемкости, полученное из квантовой статистики:
|
|
(6.4.3) |
где ![]() , то получим
, то получим
|
|
(6.4.4) |
Здесь q – дебаевская характеристическая температура (![]() ).
).
Если бы модель Дебая вполне соответствовала действительности, то единственный параметр q был бы одним и тем же для всех кристаллов, а уравнение (6.4.4) было бы универсальным соотношением. На самом деле значения q могут отличаться от экспериментальных значений температуры Дебая вплоть до 30 %.
Значения ![]() даны в табл. 6.4.1.
даны в табл. 6.4.1.
Таблица 6.4.1
|
|
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
1,0000 |
0,9995 |
0,9980 |
0,9955 |
0,9920 |
0,9876 |
0,9822 |
0,9759 |
0,9687 |
0,9606 |
|
1 |
0,9517 |
0,9420 |
0,9315 |
0,9203 |
0,9085 |
0,8960 |
0,8828 |
0,8692 |
0,8550 |
0,8404 |
|
2 |
0,8254 |
0,8100 |
0,7943 |
0,7784 |
0,7622 |
0,7459 |
0,7294 |
0,7128 |
0,6961 |
0,6794 |
|
3 |
0,6628 |
0,6461 |
0,6296 |
0,6132 |
0,5968 |
0,5807 |
0,5647 |
0,5490 |
0,5334 |
0,5181 |
|
4 |
0,5031 |
0,4883 |
0,4738 |
0,4595 |
0,4456 |
0,4320 |
0,4187 |
0,4057 |
0,3930 |
0,3807 |
|
5 |
0,3686 |
0,3569 |
0,3455 |
0,3345 |
0,3237 |
0,3133 |
0,3031 |
0,2933 |
0,2838 |
0,2745 |
|
6 |
0,2656 |
0,2569 |
0,2486 |
0,2405 |
0,2326 |
0,2251 |
0,2177 |
0,2107 |
0,2038 |
0,1972 |
|
7 |
0,1909 |
0,1847 |
0,1788 |
0,1730 |
0,1675 |
0,1622 |
0,1570 |
0,1521 |
0,1473 |
0,1426 |
|
8 |
0,1382 |
0,1339 |
0,1297 |
0,1257 |
0,1219 |
0,1182 |
0,1146 |
0,1111 |
0,1078 |
0,1046 |
|
9 |
0,1015 |
0,0985 |
0,0956 |
0,0928 |
0,0901 |
0,0875 |
0,0850 |
0,0826 |
0,0803 |
0,0780 |
|
10 |
0,0758 |
0,0737 |
0,0717 |
0,0697 |
0,0678 |
0,0660 |
0,0642 |
0,0625 |
0,0609 |
0,0593 |
|
11 |
0,0577 |
0,0562 |
0,0548 |
0,0534 |
0,0520 |
0,0507 |
0,0495 |
0,0482 |
0,0470 |
0,0459 |
|
12 |
0,0448 |
0,0437 |
0,0427 |
0,0416 |
0,0407 |
0,0397 |
0,0388 |
0,0379 |
0,0370 |
0,0362 |
|
13 |
0,0353 |
0,0346 |
0,0338 |
0,0330 |
0,0323 |
0,0316 |
0,0309 |
0,0302 |
0,0296 |
0,0290 |
|
14 |
0,0284 |
0,0278 |
0,0272 |
0,0266 |
0,0261 |
0,0255 |
0,0250 |
0,0245 |
0,0240 |
0,0235 |
|
15 |
0,0231 |
0,0226 |
0,0222 |
0,0217 |
0,0213 |
0,0209 |
0,0205 |
0,0201 |
0,0197 |
0,0194 |
|
16 |
0,0190 |
0,0187 |
0,0183 |
0,0180 |
0,0177 |
0,0173 |
0,0170 |
0,0167 |
0,0164 |
0,0161 |
|
17 |
0,0159 |
|
||||||||
|
18 |
0,0134 |
|||||||||
|
19 |
0,0114 |
|||||||||
|
20 |
0,00974 |
|||||||||
|
21 |
0,00841 |
|||||||||
|
22 |
0,00732 |
|||||||||
|
23 |
0,00640 |
|||||||||
|
24 |
0,00564 |
|||||||||
Для
решения данной задачи следует найти q
с помощью табл. 6.4.1, используя приведенное в условии значение ![]() при
при ![]() , а затем, считая q
постоянной, рассчитать величину
, а затем, считая q
постоянной, рассчитать величину ![]() для
для ![]() .
.
Получаем:
при ![]()
![]() . Вероятную точность ответа оценить нельзя, поскольку ничего
не известно о действительном распределении частот в кристалле.
. Вероятную точность ответа оценить нельзя, поскольку ничего
не известно о действительном распределении частот в кристалле.
Глава 7. Магнитные свойства твердых тел
7.1. Формула для силы
Лоренца имеет вид ![]() .
.
Для
круговой орбиты ![]() ,
, ![]() ,
, ![]() и, следовательно,
и, следовательно,
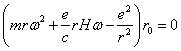 ,
,
где ![]() – единичный вектор,
совпадающий по направлению с r.
– единичный вектор,
совпадающий по направлению с r.
Решая последнее уравнение относительно w, получаем
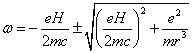 .
.
В единицах
СГС ![]() г,
г, ![]() ,
, ![]() ед. СГС,
ед. СГС, ![]() см и обычно
см и обычно ![]() кэ; отсюда
кэ; отсюда
![]() и
и ![]() .
.
Следовательно,
![]() .
.
Последний
член представляет собой угловую скорость при ![]() . Ларморовская частота задается выражением
. Ларморовская частота задается выражением
![]() .
.
7.2. Для основного состояния атома водорода
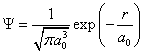 ,
,
где ![]() – радиус боровской
орбиты. Средний квадрат радиуса электронной орбиты:
– радиус боровской
орбиты. Средний квадрат радиуса электронной орбиты:
![]() ,
, ![]() .
.
Формула Ланжевена для молярной магнитной восприимчивости имеет вид
![]() .
.
Для атомарного водорода имеем
![]() .
.
7.3. Поскольку пространственное квантование отсутствует, то можно использовать классическую больцмановскую статистику.
Для намагниченности в общем случае получим
|
|
(7.3.1) |
где q – угол между m
и Н. Введем обозначения ![]() ,
, ![]() . Тогда в общем случае
. Тогда в общем случае
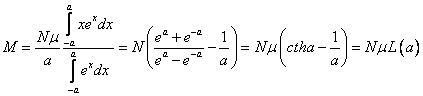 ,
,
где ![]() – функция Ланжевена.
Для
– функция Ланжевена.
Для ![]() экспоненты можно
разложить в ряд
экспоненты можно
разложить в ряд
![]()
Отсюда путем алгебраического деления многочленов находим
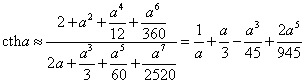 .
.
Итак, для намагниченности получим
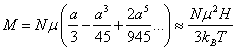 .
.
Выражение
в правой части отвечает случаю ![]() , т. е. когда члены разложения с
, т. е. когда члены разложения с ![]() и
и ![]() можно отбросить.
можно отбросить.
Этот результат можно получить также разложением экспонент подынтегральных выражений в исходном выражении (7.3.1) для М.
Глава 8. Диэлектрические свойства твердых тел
8.1. Для решения этой задачи
нужно применить теорию электростатического потенциала. Поскольку свободных
зарядов нет, то для решения задачи следует воспользоваться уравнением Пуассона ![]() . Система зарядов имеет цилиндрическую симметрию, поэтому
решения для V имеют вид
. Система зарядов имеет цилиндрическую симметрию, поэтому
решения для V имеют вид ![]() . Напряженность поля можно найти по формуле
. Напряженность поля можно найти по формуле ![]() .
.
а) Эта часть задачи упрощается, если предположить, что можно пренебречь влиянием малой полости на поле во всем объеме диэлектрического шара. Постоянные А, В и т. д. найдутся из соответствующих граничных условий.
Если
напряженность внешнего поля равна ![]() , то поле внутри шара однородно и равно
, то поле внутри шара однородно и равно ![]() , а поле внутри малой полости
, а поле внутри малой полости ![]() , откуда
, откуда
![]() .
.
Если ![]() , например
, например ![]() , то
, то ![]() .
.
У керамик электропроводность обычно очень мала, а магнитная проницаемость порядка единицы. Поэтому магнитные поля не экранируются.
б)
Внутреннее поле в лоренцевой полости можно рассматривать как результат
наложения: 1) внешнего поля; 2) деполяризующего поля ![]() , обусловленного поляризацией наружной поверхности диэлектрического
шара; 3) поля
, обусловленного поляризацией наружной поверхности диэлектрического
шара; 3) поля ![]() , обусловленного зарядами на внутренней поверхности полости
Лоренца, и наконец, 4) возможного вклада от поляризации материала внутри самой
лоренцевой полости (в этой задаче мы полагаем, что поляризация материала внутри
полости непосредственного вклада не дает).
, обусловленного зарядами на внутренней поверхности полости
Лоренца, и наконец, 4) возможного вклада от поляризации материала внутри самой
лоренцевой полости (в этой задаче мы полагаем, что поляризация материала внутри
полости непосредственного вклада не дает).
Поскольку
диэлектрик поляризован однородно, то ![]() , и результирующее поле внутри лоренцевой полости как раз
равно внешнему полю
, и результирующее поле внутри лоренцевой полости как раз
равно внешнему полю ![]() .
.
Если материал, находящийся в лоренцевой полости, не вносит непосредственного вклада в поле внутри нее, то может показаться, что результаты для случаев (а) и (б) должны быть одинаковыми. Различие получается потому, что поляризованный материал внутри полости сам поляризует диэлектрический шар снаружи от полости, в результате чего появляется добавочное поле внутри полости (обратное поле). Поляризация для обоих случаев показана на рис. 8.1.1.
|
|
|
Рис. 8.1.1. Распределение поляризации внутри диэлектрической сферы: |
В случае
(а) внутреннее поле, обусловленное поляризацией ![]() , очевидно, недостаточно для того, чтобы скомпенсировать
поле, вызванное поляризацией
, очевидно, недостаточно для того, чтобы скомпенсировать
поле, вызванное поляризацией ![]() , поэтому поле внутри полости в этом случае меньше, чем в
случае (б). Количественно разность равна просто обратному полю, обусловленному
поляризованной сферой, погруженной в диэлектрик, т. е.
, поэтому поле внутри полости в этом случае меньше, чем в
случае (б). Количественно разность равна просто обратному полю, обусловленному
поляризованной сферой, погруженной в диэлектрик, т. е.
![]() .
.
8.2. Применяя к «ящику с
шарами» на поверхности сегнетоэлектрического вещества формулу
Гаусса–Остроградского (![]() ), получаем, что там не должно быть свободных зарядов, D должно быть равно нулю, т. е.
), получаем, что там не должно быть свободных зарядов, D должно быть равно нулю, т. е. ![]() , откуда
, откуда ![]() .
.
Случайные
заряды из окружающего воздуха очень быстро оседают на поверхности, пока не
скомпенсируют заряды на поверхности, обусловленные поляризацией. Очевидно,
плотность этих зарядов должна быть равна – Р,
откуда, снова применяя ту же формулу, находим, что ![]() , т. е. в результате напряженность электрического поля падает
до нуля.
, т. е. в результате напряженность электрического поля падает
до нуля.
Кубическая
решетка с параметром 4 Å содержит ![]() ионов титана на 1 м3.
Заряд каждого из них равен
ионов титана на 1 м3.
Заряд каждого из них равен ![]() К, так что в принципе
поляризация в 0,25 К/м2 должна была бы получиться от сдвига ионов
титана примерно на 0,25 Å.
К, так что в принципе
поляризация в 0,25 К/м2 должна была бы получиться от сдвига ионов
титана примерно на 0,25 Å.
Дипольный
момент на одну элементарную ячейку равен, очевидно, поляризации Р, деленной на число ячеек, содержащихся
в 1 м3, т. е. около ![]() , или 4,8D. Перовскитная структура
титаната бария такова, что локальное поле у ионов Ti4+ гораздо больше, чем поля
у ионов в большинстве других веществ, а поэтому и возникает необычайно большая
поляризация.
, или 4,8D. Перовскитная структура
титаната бария такова, что локальное поле у ионов Ti4+ гораздо больше, чем поля
у ионов в большинстве других веществ, а поэтому и возникает необычайно большая
поляризация.
8.3. Электростатическая
энергия диэлектрика (в Дж) по определению равна интегралу ![]() , а в переменном гармоническом поле энергия, выделяемая за
один период, равна площади петли гистерезиса в координатах D – E.
, а в переменном гармоническом поле энергия, выделяемая за
один период, равна площади петли гистерезиса в координатах D – E.
У данного
сегнетоэлектрика эта петля прямоугольная, и площадь ее в одном квадранте равна ![]() , т. е. площадь всей петли равна
, т. е. площадь всей петли равна ![]() . Поэтому, если температура падает ниже
. Поэтому, если температура падает ниже ![]() , то энергия, рассеиваемая за один период, будет равна
, то энергия, рассеиваемая за один период, будет равна ![]() , или
, или ![]() при понижении
температуры на 1 градус. Это вполне пригодная для практики система стабилизации
температуры, но она, конечно, ограничена температурами Кюри доступных сегнетоэлектриков.
при понижении
температуры на 1 градус. Это вполне пригодная для практики система стабилизации
температуры, но она, конечно, ограничена температурами Кюри доступных сегнетоэлектриков.
Глава 9. Основы зонной теории твердого тела
9.1. Уравнение Шредингера для этого случая имеет вид
![]() , где
, где ![]() .
.
Это
дифференциальное уравнение второго порядка имеет два независимых решения ![]() и
и ![]() . Если какая-либо функция
. Если какая-либо функция ![]() является решением
этого уравнения, то функция
является решением
этого уравнения, то функция ![]() также является его
решением. В общем случае
также является его
решением. В общем случае
![]() ,
,
![]() ,
,
где a – константы, определяемые величинами Е и V, входящими в это уравнение.
Искомое
решение ![]() , очевидно, является линейной комбинацией
, очевидно, является линейной комбинацией ![]() и
и ![]() :
:
![]() .
.
Таким образом,
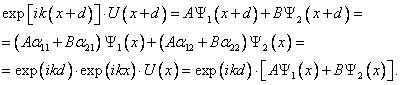
Приравнивая
коэффициенты при ![]() и
и ![]() , получаем систему уравнений для нахождения А и В:
, получаем систему уравнений для нахождения А и В:
![]() ,
,
![]()
Для того чтобы эта система имела
нетривиальные решения, детерминант, составленный из коэффициентов при А и В,
должен обращаться в нуль, т. е.
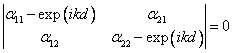 .
.
Это квадратное относительно exp(ikd) уравнение,
имеющее два корня, которые соответствуют двум независимым решениям. Значения k, определяемые этим квадратным
уравнением, будут вещественными или комплексными в зависимости от значений Е. Совокупность
решений с вещественными значениями k соответствует функциям Блоха.
Отметим, что должны существовать и
другие решения, и они полезны при обсуждении таких состояний, как связанные
состояния на свободной поверхности твердого тела. Однако они не соответствуют
стационарным состояниям электронов в решетке. Значения k определены с
точностью до слагаемого ![]() , где п – целое число. В случае трехмерной
решетки волновой вектор электрона k определен с точностью до
, где п – целое число. В случае трехмерной
решетки волновой вектор электрона k определен с точностью до ![]() , где
, где ![]() удовлетворяет
условию
удовлетворяет
условию ![]() , р – целое
число,
, р – целое
число, ![]() – векторы решетки.
Таким образом, мы должны рассмотреть только значения k, лежащие внутри или на поверхности
ячейки (в общем случае многогранника), образованной плоскостями, которые делят
пополам линии, соединяющие узел решетки с его «ближайшими соседями», соседями
«ближайших соседей» и т. д. Эта ячейка называется первой зоной Бриллюэна.
– векторы решетки.
Таким образом, мы должны рассмотреть только значения k, лежащие внутри или на поверхности
ячейки (в общем случае многогранника), образованной плоскостями, которые делят
пополам линии, соединяющие узел решетки с его «ближайшими соседями», соседями
«ближайших соседей» и т. д. Эта ячейка называется первой зоной Бриллюэна.
Для гранецентрированной кубической решетки обратная
решетка – объемноцентрированный куб, и для этой структуры зона Бриллюэна
представляет собой ячейку Вигнера–Зейтца.
Если k ограничено
значениями внутри или на поверхности зоны, общее выражение запишется в виде ![]() , где
, где ![]() – произвольный вектор
обратной решетки.
– произвольный вектор
обратной решетки.
9.2. В
одномерной решетке с периодом d границы зон соответствуют следующим значениям k:
![]() . Уравнение
Вульфа–Брэгга
. Уравнение
Вульфа–Брэгга ![]() для одномерного случая
можно записать в виде:
для одномерного случая
можно записать в виде: ![]() , а поскольку
, а поскольку ![]() , то
, то ![]() (где
(где ![]() ).
).
В
трехмерном случае энергетические разрывы энергии соответствуют таким значениям k, для которых ![]() . Вектор
. Вектор ![]() связан с миллеровскими
индексами (
связан с миллеровскими
индексами (![]() ) плоскостей кристалла соотношением
) плоскостей кристалла соотношением ![]() . Таким образом,
. Таким образом, ![]() , где
, где ![]() , что сразу дает условие брэгговского отражения электронных
волн.
, что сразу дает условие брэгговского отражения электронных
волн.
9.3.
Эта задача была впервые
поставлена и решена Кронигом и Пенни. Когда потенциал U равен нулю,
решениями уравнения Шредингера являются плоские волны ![]() ,
, ![]() , где
, где ![]() .
.
Волновая функция представляет собой линейную
комбинацию этих решений:
![]() .
.
В области, где потенциал V имеет постоянную и отличную от нуля величину, волновую функцию можно записать в виде
![]() ,
,
![]() .
.
Эти функции будут собственными функциями уравнения при
положительных значениях Е, так что величина a является вещественной; однако величина b может быть как вещественной, так и
мнимой.
Значения Е определяются граничными
условиями в начале координат, где волновая функция и ее производная должны быть
непрерывными, и, разумеется, также требованием ограничиться классом решений
типа блоховских функций:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Эти условия дают совместное уравнение для Е и k:
для ![]()
![]()
и для ![]()
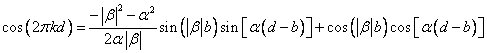 .
.
Собственные значения, соответствующие потолку верхней зоны и дну второй зоны, соответственно равны 2,32 и 4,31 эВ.
9.4.
Рис. 9.4.1, а представляет собой картину
изменения энергии в зоне вдоль одного направления в k-пространстве.
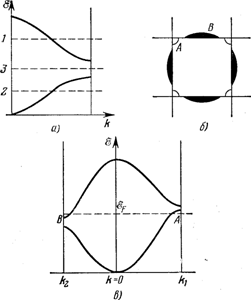
Отсюда находим, что если число валентных электронов на атом является
достаточным, чтобы заполнить состояния так, чтобы уровень Ферми (пунктир)
проходил, как в случаях 1 или 2, то вещество является металлом.
Если уровень Ферми проходит, как показано в случае 3, т. е. находится внутри запрещенной зоны, то вещество является
диэлектриком.
Для того чтобы кристалл был
диэлектриком, уровень Ферми должен оказываться в запрещенной зоне для всех
значений k. Далее, для
большинства диэлектриков имеется широкая, порядка нескольких электрон-вольт,
энергетическая щель между валентной зоной и зоной проводимости. Если
энергетическая щель узкая, так что электроны могут при тепловом возбуждении
преодолевать ее непосредственно или при помощи примесей (электроны могут занимать энергетические уровни
примесных атомов внутри щели) и, следовательно, попасть в итоге в зону
проводимости, то вещество обладает полупроводниковыми свойствами.
Для металлов мы можем изобразить в k-пространстве поверхность, которая является
поверхностью постоянной энергии на границе Ферми. Для двумерного случая,
показанного на рис. 9.4.1, б и в, энергетические зоны и поверхности Ферми
изображены для направлений [10] и [11].
|
|
|
Рис. 9.4.1. Энергетические зоны и поверхности Ферми, иллюстрирующие
свойства твердых тел: а −
металлические; б − диэлектрические; в − полупроводниковые |
В данном случае так называемые карманы – совокупность занятых состояний во второй зоне Бриллюэна (зачерненные области В) – в то же время приводят к появлению «пустых» карманов – совокупности незанятых состояний (дырок, обозначенных буквой А). Оба типа карманов образуются обычно вблизи границ зоны, где ход изменения энергии в зоне заметно отличается от параболического и где эффективная масса значительно отличается от массы свободного электрона. Вследствие близости карманов к запрещенным областям энергии число эффективных носителей тока в таких случаях невелико.
Глава 10. Электрические свойства твердых тел
10.1. Концентрация собственных носителей заряда ni имеет сильную температурную зависимость и определяется соотношением
|
|
(10.1.1) |
где эффективная плотность состояний в C- и V-зонах NC,V также зависит от температуры T и эффективной массы плотности состояний m*:
|
|
(10.1.2) |
Ширина запрещенной зоны Eg имеет слабую зависимость от температуры типа Eg = Eg0 – αТ. Величины Eg0 и α приведены в табл. 9.1, 9.2, в табл. 5 приложения указаны величины NC и NV при Т = 300 K. Расчетные значения эффективной плотности состояний в C- и V-зонах NC, NV и концентрации собственных носителей заряда ni при температуре жидкого азота Т = 77 K приводится ниже
|
Полупроводник |
Si |
Ge |
GaAs |
InSb |
|
Параметры |
||||
|
NC, см-3 |
3,6·1018 |
1,04·10110 |
5,8·1016 |
5,1·1015 |
|
NV, см-3 |
1,4·1018 |
6,10·1018 |
10,8·1017 |
1,5·1018 |
|
ni, см-3 |
3·10-20 |
1,4·10-7 |
2,8·10-33 |
1,2·1010 |
10.2. Примесь
полностью ионизована, когда концентрация равновесных электронов равна
концентрации легирующей примеси n0 = ND.
Из основного соотношения для полупроводников: n0·p0 = ni2 найдем концентрацию неосновных
носителей заряда ![]() . Для Si p0 = 2,6·103, для GaAs p0 = 1,2·10-3 см-3.
. Для Si p0 = 2,6·103, для GaAs p0 = 1,2·10-3 см-3.
10.3. Вырождение в полупроводнике наступает, когда уровень Ферми F приближается к C‑ или V‑зоне на расстояние порядка kBT, т. е. F – EV = kBT. В случае полной ионизации примеси концентрация дырок p рассчитывается по соотношению
|
|
(10.3.1) |
и определяется уровннем легирования NA: NA = p = NV/2,73. Следовательно, концентрация акцепторов при которой наступает вырождение равняется для Si: NA = 3,8·1018 см-3, для Ge: NA = 2,2·1018 см-3.
10.4. Величину удельного сопротивления ρ найдем из соотношения
![]()
учитывая условие полной ионизации примеси.
p‑тип: p0 = NA; n‑тип, n0 = ND
![]()
![]()
![]()
10.5. В собственном полупроводнике удельная
электропроводность определяется уравнением σi = qnμn + qpμp = qni(μn + μp). Удельное сопротивление будет ρi = 1/σi. Подставляя табличные значения параметров из табл. 5
Приложения, получаем
|
Полупроводник |
Si |
Ge |
GaAs |
InSb |
|
ρi, Ом·см |
1,9·105 |
43 |
6,4·107 |
4·10-3 |
Глава 11. Оптические свойства твердых тел
11.1. Время жизни τ0 рассчитаем, используя формулу (11.18). Получаем τ0 =1.10–8 с, концентрации неравновесных носителей заряда равны n = ND = 1016 см-3 и p = G·τ0 = 1013 см-3.
11.2. Коэффициент рекомбинации r получим из соотношения G = R = r·n·p.
![]() .
.
Отсюда
имеем для r: ![]() .
.
r = 1·10-8 см3c-1, избыточная концентрация электронов Δn = G·τ0 = 5·1012 см-3.
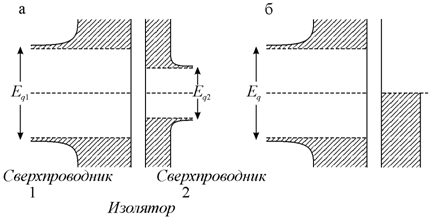
Глава 12. Сверхпроводимость
12.1.
Учитывая, что ![]() , индуктивность проволочного кольца можно считать равной
индуктивности прямого провода длиной
, индуктивность проволочного кольца можно считать равной
индуктивности прямого провода длиной ![]() . Для одиночного провода длиной l
индуктивность единицы длины легко оценить: поле от тока I по
теореме о циркуляции на расстоянии R равно
. Для одиночного провода длиной l
индуктивность единицы длины легко оценить: поле от тока I по
теореме о циркуляции на расстоянии R равно ![]() , а поток через площадку единичной длины и ширины (считаем,
что поле спадает на расстоянии порядка l) равен
, а поток через площадку единичной длины и ширины (считаем,
что поле спадает на расстоянии порядка l) равен ![]() . Таким образом?
. Таким образом? ![]() , а для большого кольца
, а для большого кольца
![]() /
/
Изменение запасенной магнитной энергии равно омическим потерям
![]() или
или ![]() .
.
Откуда
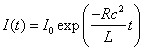 и
и ![]() Ом.
Ом.
12.2.
Величина критического поля для олова при 2 К может быть рассчитана из
следующего приближенного соотношения: 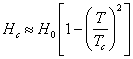 . Подставляя в это соотношение величины, данные в условии
задачи, находим при 2 К
. Подставляя в это соотношение величины, данные в условии
задачи, находим при 2 К ![]() Э.
Э.
Величина
тока, который может протекать в оловянной проволоке, находящейся в
сверхпроводящем состоянии, может быть найдена по правилу Силсби. Магнитное поле
на поверхности проволоки радиусом r, индуцируемое током I, равно ![]() . Таким образом, при 2 К для проволоки с
. Таким образом, при 2 К для проволоки с ![]() см
см
![]() .
.
Еще раз
используя правило Силсби, находим, что диаметр проволоки может быть увеличен до
![]() , если значение критического тока увеличивается до
, если значение критического тока увеличивается до ![]() .
.
Следует отметить, что плотность критического тока в сверхпроводниках первого рода уменьшается с увеличением диаметра проволоки, а критический ток пропорционален диаметру проволоки, а не площади ее поперечного сечения.
12.3.
Вольт-амперную характеристику можно понять, обращаясь к диаграммам энергии,
представленным на рис. 12.3.1.
|
|
|
Рис. 12.3.1. Энергетические диаграммы для туннельных контактов: |
Возможно,
что легче сначала разобраться в ситуации, когда сверхпроводник находится в
контакте с нормальным металлом; контакт осуществляется через непроводящий слой,
как это показано на рис. 12.3.1, б. При абсолютном нуле туннельный ток будет
отсутствовать до тех пор, пока напряжение не достигнет примерно величины ![]() . Тогда
заполненные состояния на одной стороне контакта будут находиться против
незаполненных состояний на другой его стороне и ток с возрастанием напряжения
будет быстро расти. При температурах, отличных от 0 К, некоторые возбужденные
электроны оказались бы выше энергетической щели и при разности потенциалов,
меньшей чем
. Тогда
заполненные состояния на одной стороне контакта будут находиться против
незаполненных состояний на другой его стороне и ток с возрастанием напряжения
будет быстро расти. При температурах, отличных от 0 К, некоторые возбужденные
электроны оказались бы выше энергетической щели и при разности потенциалов,
меньшей чем![]() , наблюдался бы туннельный ток, что и
показано на диаграмме. Однако экстраполированное значение напряжения
, наблюдался бы туннельный ток, что и
показано на диаграмме. Однако экстраполированное значение напряжения ![]() равно
равно ![]() .
.
Как видно из рис. 12.3.1, а, случай, когда контактный слой находится между двумя
различными сверхпроводниками, несколько отличается от предыдущего. Некоторые
электроны возбуждаются, проходя энергетическую щель с одной стороны контактного
слоя, и поэтому ток будет медленно возрастать с ростом напряжения, при этом
максимум тока будет достигнут при напряжении ![]() , поскольку
частично заполненные состояния будут находиться друг против друга. При
дальнейшем увеличении напряжения ток будет уменьшаться до тех пор, пока
напряжение не станет равным
, поскольку
частично заполненные состояния будут находиться друг против друга. При
дальнейшем увеличении напряжения ток будет уменьшаться до тех пор, пока
напряжение не станет равным ![]() , когда
заполненные состояния с одной стороны контактного слоя будут появляться против
незаполненных состояний с другой его стороны. С этого момента ток быстро растет
с напряжением.
, когда
заполненные состояния с одной стороны контактного слоя будут появляться против
незаполненных состояний с другой его стороны. С этого момента ток быстро растет
с напряжением.
Мы видим, что можно определить
величину напряжений ![]() и
и ![]() и соответственно
значения
и соответственно
значения ![]() и
и ![]() .
.
Таким образом, для сверхпроводников свинца и алюминия
при 0 К значения ширины энергетической щели соответственно равны ![]() и
и ![]() эВ.
эВ.
Согласно теории БКШ, при 0 К ширина
энергетической щели равна ![]() . Принимая во внимание, что величины энергетических
щелей при 0,5 и 0 К отличаются незначительно, мы получаем, что Тс
свинца и алюминия соответственно лежат около 8,9 и 1,1 К. Один из
сверхпроводников (алюминий) при 1,1 К переходит в нормальное состояние, так что
при этой температуре будут исчезать максимумы и минимумы, показанные на рис.
12.20.
. Принимая во внимание, что величины энергетических
щелей при 0,5 и 0 К отличаются незначительно, мы получаем, что Тс
свинца и алюминия соответственно лежат около 8,9 и 1,1 К. Один из
сверхпроводников (алюминий) при 1,1 К переходит в нормальное состояние, так что
при этой температуре будут исчезать максимумы и минимумы, показанные на рис.
12.20.
Глава 14. Поверхностные и контактные явления в твердых телах
14.1. Дебаевская длина характеризует глубину проникновения электрического поля в полупроводник при малых возмущениях потенциала порядка kBT/q:
|
|
(14.1.1) |
Зная ND = 2,8·1014 см-3, получаем из (14.1.1) значение LD = 2,5·10-5 см = 0,25 мкм.
При больших величинах обедняющих напряжений глубина проникновения электрического поля W обычно много больше длины Дебая, поскольку
![]() и
и 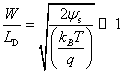 .
.
14.2. Для собственных полупроводников дебаевская длина экранирования LD определяется диэлектрической постоянной εs и собственной концентрацией ni.. Используя значения этих параметров из табл. 5 приложения, получаем после подстановки в (14.1.1)
|
Полупроводник |
Si |
Ge |
GaAs |
InSb |
|
LD, мкм |
33 |
0,96 |
1200 |
0,035 |
Следовательно, дебаевская длина экранирования возрастает с ростом ширины запрещенной зоны полупроводника.
14.3. Значения
поверхностной концентрации ns и ps в классическом случае выражаются следующим образом: ![]() и
и ![]() . Рассчитаем необходимые параметры:
. Рассчитаем необходимые параметры:
![]() .
.
n0 = 4,2·1015 см-3, p0 = 6,1·104 см-3, 2φ0 =0,65 эВ.
|
ψs, эВ |
0,3 |
–0,2 |
–0,5 |
–0,9 |
|
ns, см-3 |
4,5Ч1020 |
1,9Ч1012 |
1,7Ч107 |
3,4Ч10-3 |
|
ps, см-3 |
5,0Ч10-1 |
1,2Ч108 |
1,3Ч1013 |
6,5Ч1019 |
Сравнивая значения ns и ps со значениями n0
и p0, получаем, что
состояние:
1 – обогащение, 2 – обеднение, 3 – слабая инверсия, 4 – сильная инверсия.
14.4. Заряд в ОПЗ Qsc в общем случае записывается как
|
|
(14.4.1) |
где LD – длина экранирования Дебая,
функция F(ψs, φ0) для
невырожденного полупроводника p‑типа:
|
|
(14.4.2) |
Емкость ОПЗ Csc также выражается через F(ψs, φ0):
|
|
(14.4.3) |
Для частных случаев: обогащения (ψs < 0), обеднения (φ0 > ψs > 0), слабой (2φ0 > ψs > φ0) и сильной (ψs > 2φ0) инверсии можно использовать упрощенные выражения из гл. 14 (14.80 – 14.85). Объемное положение уровня Ферми относительно середины запрещенной зоны вычислим по формуле (14.73). Расчет дает значение φ0 = 0,29 эВ. После подстановки параметров в уравнение (14.4.1) и (14.4.3) получаем
ψs |
Qsc, Кл/см2 |
Csc, Ф/см2 |
|
0,
плоские зоны |
0 |
8,0·10-8 |
|
φ0,
середина зоны |
9,3.10-9 |
5,7.10-8 |
|
2φ0, пороговый потенциал |
1,4.10-8 |
1.7.10-8 |
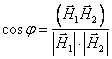 .
. .
. .
.
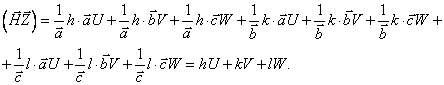
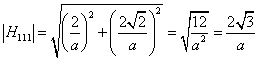 .
.
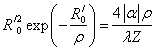 .
.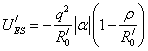 .
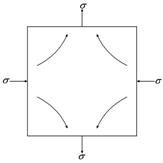
.
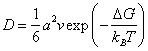 ,
,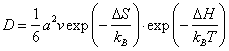 .
.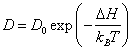 ,
,
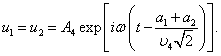
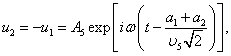
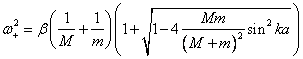 ,
,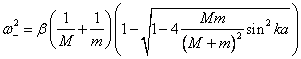 .
. .
. .
. ,
, ,
,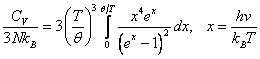 .
.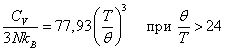
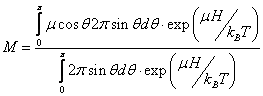 ,
,
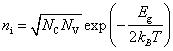 ,
,