5.5. Колебания атомов трехмерной решетки

Количественный анализ колебаний атомов в трехмерной решетке представляет собой очень сложную задачу. Допустим, что трехмерная решетка состоит из одинаковых атомов массой M и на объем V кристалла приходится N элементарных ячеек (примитивных). Поскольку каждый атом в решетке имеет три степени свободы, то весь кристалл имеет 3N степеней свободы. Вектор смещения j-го атома:

,

(5.53)

где A_к − амплитуда колебаний, − единичный вектор поляризации нормальной моды, описывающий направление, в котором движутся атомы, − радиус-вектор j-го атома, находящегося в равновесии.

Решая систему из 3N уравнений движения и подставляя в них решения (5.53), относительно A_к для каждого значения волнового вектора можно получить три моды колебаний, которые определяют три ветви дисперсионных соотношений.

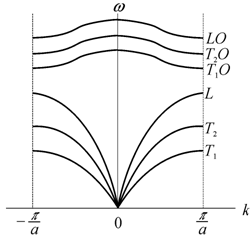
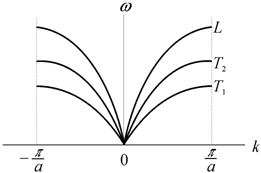
Одна из трех мод L соответствует продольной волне, а две другие T₁ и T₂ – поперечным волнам (рис. 5.11). Для нахождения интервала изменения и определения числа допустимых значений k пользуются периодическими граничными условиями.

Рис. 5.11. Дисперсионная кривая для примитивной трехмерной решетки Бравэ [59]

Предположим, что кристалл имеет форму прямоугольного параллелепипеда с ребрами , , (где , , , − векторы трансляций кристаллической решетки). , , – большие целые числа. Тогда для смещения вдоль j-й оси можно записать

.

(5.54)

Следовательно, разрешенные значения векторов должны удовлетворять условию

,

(5.55)

а разрешенные значения волновых чисел вдоль j-й оси

,

(5.56)

где n_j – целое число.

Разрешенные значения волновых векторов, пользуясь соотношением (5.56), можно представить в виде

,

(5.57)

где - вектора элементарных трансляций обратной решетки кристалла . Число допустимых значений волновых векторов в пределах первой зоны Бриллюэна равно числу элементарных ячеек N в кристалле. При этом разрешенные значения волновых чисел k равномерно распределены в k -пространстве с плотностью .

Для колебаний трехмерной решетки с базисом, где на элементарную ячейку приходится r атомов и система имеет 3rN степеней свободы, решение системы из 3rN уравнений приводит к существованию 3r ветвей колебаний. В этом случае дисперсионное соотношение этих ветвей будет иметь вид

.

(5.58)

Три нижние ветви называют акустическими, а остальные (3r-3) являются оптическими (рис. 5.12). Среди оптических колебаний также имеются ветвь продольных LО и две ветви поперечных T₁О и T₂O колебаний.

Рис. 5.12. Дисперсионные кривые для трехмерной решетки с базисом [59]

Таким образом, в случае решетки с базисом движения атомов могут быть представлены в виде суперпозиции 3rN колебаний, или мод.

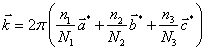Назад Далее...