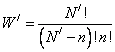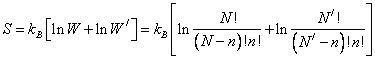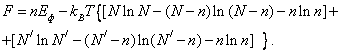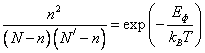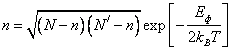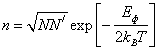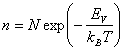3.2.3. Термодинамика точечных дефектов

Образование точечных дефектов связано со значительными затратами энергии. Эта энергия напрямую зависит от сил межатомного взаимодействия в твердом теле и от типа дефекта. Например, для образования одной вакансии в германии требуется энергия около 2 эВ, а в кремнии − примерно 2,3 эВ. Несмотря на это, существование дефектов в кристалле при относительно высоких температурах является энергетически выгодным, т. к. образование дефектов не только увеличивает внутреннюю энергию кристалла, но, как будет показано ниже, увеличивает и энтропию, зависящую от степени беспорядка в расположении атомов [74].

Свободная энергия для заданной температуры T определяется по формуле:

,

(3.1)

где Е − внутренняя энергия, S − энтропия системы.

Свободная энергия будет стремиться к минимальному значению при некоторой концентрации дефектов, что определяется балансом ее энергетической и энтропийной составляющей. Если в кристалле могут возникать дефекты и по Френкелю, и по Шоттки, то будут преобладать те из них, для образования которых требуется меньше затрат энергии.

Для установления зависимости количества возникающих в определенном твердом теле вакансий от температуры примем ряд допущений, состоящих в том, что: в кристалле имеется только один тип дефектов; объем кристалла не зависит от температуры; дефекты не зависят друг от друга и частота колебаний атомов не зависит от наличия дефектов.

Обозначим  – энергию образования пары Френкеля, а N и  - соответственно количества атомов и междоузлий в кристалле. Пусть при некоторой термодинамической температуре Т из узлов в междоузлия вышло n атомов, что привело к возникновению n вакансий. Образование дефектов влечет за собой разупорядочение структуры кристалла, а значит и рост энтропии S [54]:

.

(3.2)

Здесь  − постоянная Больцмана, а W – термодинамическая вероятность, которая представляет собой число способов, которыми может быть осуществлено данное состояние системы. Такую энтропию называют конфигурационной, т. к. она связана с распределением атомов в твердом теле. Число способов, которыми n вакансий может быть распределено по N узлам решетки, составляет

.

(3.3)

Аналогично для n атомов, попадающих в  междоузлий:

.

(3.4)

Увеличение энтропии в результате образования пар Френкеля можно представить в следующем виде:

.

(3.5)

Используя разложение Стирлинга для величины ln(x!), которое имеет вид , из выражения (3.5) получим

.

(3.6)

Если на образование одного дефекта затрачивается энергия , то увеличение внутренней энергии кристалла при образовании n дефектов составит . Тогда для свободной энергии получим следующее выражение:

.

(3.7)

В состоянии теплового равновесия свободная энергия должна быть минимальна по отношению к изменению n, т. е. должно выполняться условие

.

(3.8)

Подставив в эту формулу выражение (3.7) и проводя преобразования, получим

(3.9)

или

.

(3.10)

Отсюда можно найти число пар Френкеля

.

(3.11)

 

Если учесть, что  и , то

.

(3.12)

Если N и  являются соответственно числами узлов и междоузлий, приходящихся на единичный объем, то n представляет собой концентрацию пар Френкеля. Очевидно, что при T = 0 K концентрация пар Френкеля нулевая, а при росте температуры концентрация растет по экспоненте.

Аналогичные рассуждения в случае дефектов по Шоттки приводят к выражению для концентрации этих дефектов

,

(3.13)

где   − энергия образования вакансии.

В отличие от формулы (3.12), здесь под знаком экспоненты нет множителя 1/2. Это объясняется тем, что при расчете концентрации пар Френкеля учитывается образование дефектов двух типов в равных количествах.

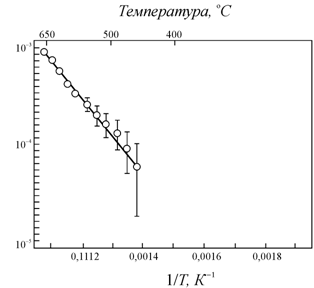
Экспериментальная проверка формулы (3.13) показывает, что этот закон достаточно точно выполняется. Например, для алюминия (рис. 3.5), где энергия образования вакансии  составляет 0,75 эВ, оказывается, что при температуре плавления на каждую тысячу атомов приходится одна вакансия, а при комнатной температуре − одна вакансия на 10¹² атомов.

 

 

Вообще отношение 1:1000 характерно для металлов вблизи температуры плавления. При комнатной температуре количество вакансий в таких металлах, как серебро и медь, еще меньше, чем у алюминия, за счет больших значений энергии образования вакансий   и температуры плавления. Однако, несмотря на столь малые концентрации, вакансии оказывают большое влияние на свойства твердых тел.