10.5. Энергия Ферми. Критерий вырождения электронного газа

В предыдущих рассуждениях считалось, что энергетическое положение уровня Ферми задано. Рассмотрим, как можно найти значение энергии Ферми, если задана концентрация свободных носителей n₀, p₀ и температура T.

Для собственного полупроводника уравнение электронейтральности приобретает вид p – n = 0 или p = n. Если ширина запрещенной зоны полупроводника достаточно велика (E_g много больше k_BT) и если эффективные массы электронов m_n и дырок m_p одного порядка, то уровень Ферми будет достаточно удален от краев зон (E_C – F > 2k_BT и F – E_V > 2k_BT), и полупроводник будет невырожденным.

Приравнивая значения концентраций электронов и дырок из соотношений (10.15) и (10.18), получаем

.

(10.27)

Отсюда вычисляем значение энергии Ферми F. Уравнение (10.27) – уравнение первого порядка относительно . Решение уравнения (10.27) дает выражение для энергии Ферми

(10.28)

где через  обозначена энергия середины запрещенной зоны. При выводе  в правом выражении для энергии Ферми F отношение эффективных плотностей состояний (N_C/N_V) была заменена на отношение эффективных масс (m_n/m_p) с использованием уравнения (10.16).

Для случая m_n^* = m_p^* энергия Ферми в собственном полупроводнике находится посреди запрещенной зоны

.

(10.29)

Если известны концентрации носителей заряда n и p в зонах, то значение энергии Ферми F можно определить из формул (10.15) и (10.18). Так, для невырожденного полупроводника n‑типа имеем:

.

(10.30)

Аналогично для невырожденного полупроводника p‑типа

.

(10.31)

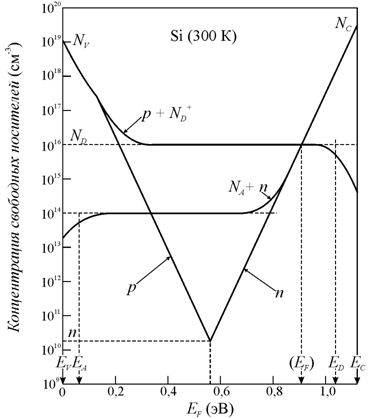
Из выражений (10.30, 10.31) видно, что чем больше концентрация основных носителей, тем ближе уровень Ферми к краю соответствующей зоны (рис. 10.12). Для донорного полупроводника в случае полной ионизации примеси концентрация электронов равна концентрации донорной примеси n₀ = N_D. Тогда

.

(10.32)

Для акцепторного полупроводника концентрация дырок равна концентрации акцепторной примеси p₀ = N_A (10.24), тогда

.

(10.33)

 

Рис. 10.12. Зависимость энергии Ферми F от концентрации свободных носителей в кремнии [9]

 

Как уже отмечалось, вырожденный и невырожденный электронный газ описывается соответственно статистикой Ферми−Дирака и Больцмана. Квантовая статистика переходит в классическую, если энергия состояния: . Следовательно,  вырождение в полупроводнике наступает тогда, когда энергия Ферми F приближается к дну зоны проводимости или к потолку валентной зоны на расстояние порядка k_ВT, т. е. для полупроводника p-типа: F – E_V = k_ВТ. В случае полной ионизации примеси в акцепторном полупроводнике концентрация дырок p определяется как

.

(10.34)

Отсюда следует критерий вырождения электронного газа: по мере роста концентрации свободных носителей (по мере роста легирующей примеси) полупроводник становится вырожденным, если концентрация свободных носителей сравняется с эффективной плотностью состояний. Более точно, с учетом соотношения E – , получаем  для критерия вырождения N_A = p = N_V/2,73. Используя для классических полупроводников кремния и германия табличные значения эффективной плотности состояний, получаем количественную оценку концентрации свободных носителей, после которых наступает вырождение: для Si p = 3,8·10¹⁸ см^-3, для Ge p = 2,2·10¹⁸ см^-3.

В металлах энергия Ферми находится внутри зоны проводимости, поэтому электронный газ в металлах всегда вырожден. Ниже, в табл. 10.1, показано значение энергии Ферми и волнового вектора, соответствующего энергии Ферми, для некоторых металлов [86, 89].

 

Таблица 10.1

Энергия Ферми и волновой вектор, соответствующий этой энергии для простых металлов

Металл	F (эВ)	k (108/см)	Металл	F (эВ)	k (108/см)
Li	4,74	1,12	Fe	11,1	1,71
Na	3,24	0,92	Mn	10,9	1,70
K	2,12	0,75	Zn	9,47	1,58
Rb	1,85	0,70	Cd	7,47	8,68
Cs	1,59	0,65	Hg	7,13	1,37
Cu	7,00	1,36	Al	11,7	1,75
Ag	5,49	1,20	Ga	10,4	1,66
Au	5,53	1,21	In	8,63	1,51
Be	14,3	1,94	Tl	8,15	1,46
Mg	7,08	1,36	Sn	10,2	1,64
Ca	4,69	1,11	Pb	9,47	1,58
Sr	3,93	1,02	Bi	9,9	1,61
Ba	3,64	0,98	Sb	10,9	1,70
Nb	5,32	1,18

 

Эти значения являются полезными для практических случаев, поскольку энергия Ферми определяет термодинамическую работу выхода, а волновой вектор определяет энергетическое положение уровня Ферми относительно дна разрешенной зоны энергий.
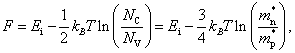
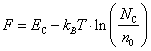
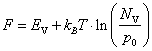
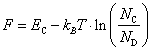
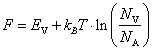
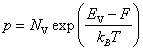