Рентгеноструктурный анализ аморфных материалов
3.3. Нормировка кривых распределения интенсивности рассеяния
Наиболее распространенными методиками нормировки кривых распределения интенсивности являются метод Крог-Моэ и Нормана [23,24] и Вайнштейна [5,6,25 ].
Метод Вайнштейна основан на законе сохранения интенсивности: суммарная интенсивность рассеяния конфигурацией из определенного числа атомов не зависит от их взаимного расположения, то есть от того, образуют они кристалл, жидкость или газ. Интерференция волн, рассеянных различными атомами данной конфигурации, приводят только к перераспределению интенсивности рассеяния, усилению ее в одних направлениях и ослаблению в других. Отсюда следует, что интеграл от нормированных экспериментальных значений интенсивности по всем возможным значениям К будет равен аналогичному интегралу от значений интенсивности, даваемых системой невзаимодействующих атомов :
![]()
V* - объем обратного пространства. Сумма по n - сумма по всем атомам данной конфигурации, Ikn( К) - величина интенсивности комптоновского рассеяния для n -го атома; k - коэффициент нормировки.
Изотропия рассматриваемых объектов обуславливает изотропию рассеяния ими рентгеновских лучей и позволяет заменить интегрирование по объему обратного пространства V* на интегрирование по модулю дифракционного вектора:
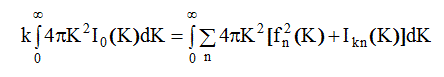
Одновременно удобно перейти в правой части от суммирования по всем атомам скопления к суммированию по единице состава.
Тогда
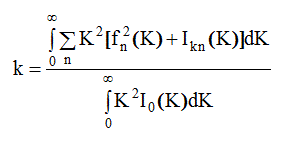 (3.14)
(3.14)
Соответственно интенсивность когерентного рассеяния в электронных единицах на формульную единицу
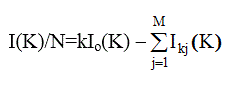 (3.15)
(3.15)
Вывод коэффициента нормировки, выполненный Крог-Моэ и Норманом основан на совершенно иных предположениях. Авторы [23, 24] исходили из формулы (2.56), которую, поделив обе части на 4π r2 , можно переписать в виде:
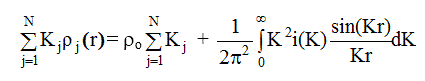 (3.16)
(3.16)
Радиальное распределение электронной плотности любой системы стремится к 0 при r→0 ; ![]() при этом стремится к 1.
Следовательно, в пределе близких к нулю значений расстояний r формулу (3.16) следует записать в виде:
при этом стремится к 1.
Следовательно, в пределе близких к нулю значений расстояний r формулу (3.16) следует записать в виде:
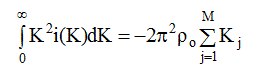 (3.17)
(3.17)
Исходя из (2.54) для i( К), получаем
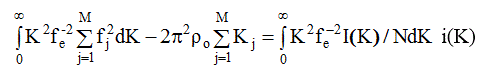
Так как, согласно (3.15) 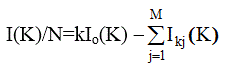 , то коэффициент нормировки
, то коэффициент нормировки
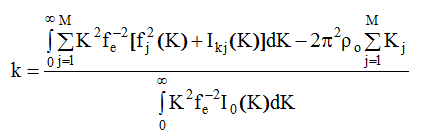 (3.18)
(3.18)
Показано [5], что для всех веществ 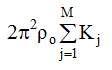 << по величине, чем интеграл, стоящий в числителе, следовательно, формулы (3.14) и (3.18) для многокомпонентных
систем различается наличием в числителе и знаменателе множителя fe-2 (К ). Для однокомпонентных систем формулы (3.14) и (3.18) практически совпадают.
Уоррен [10 ] , используя те же самые предположения, что и авторы работ [23, 24], вывел выражение для k , исходя из формулы (2.66). Разделим обе части уравнения (2.66) на к
и устремим r → 0, тогда
<< по величине, чем интеграл, стоящий в числителе, следовательно, формулы (3.14) и (3.18) для многокомпонентных
систем различается наличием в числителе и знаменателе множителя fe-2 (К ). Для однокомпонентных систем формулы (3.14) и (3.18) практически совпадают.
Уоррен [10 ] , используя те же самые предположения, что и авторы работ [23, 24], вывел выражение для k , исходя из формулы (2.66). Разделим обе части уравнения (2.66) на к
и устремим r → 0, тогда
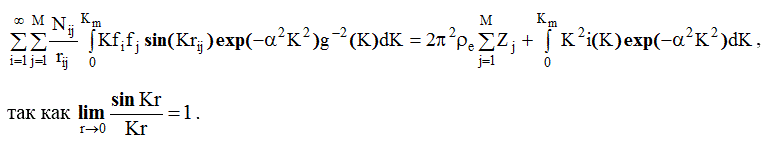 (3.19)
(3.19)
Уоррен показал, что максимальное значение левой части уравнения много меньше значения суммы, стоящей в правой части. Строгая оценка приводит к следующим результатам. Используя большой коэффициент сходимости, такой, что α2K2max = 4, можно предел интегрирования в левой части продлить до ∞. Поскольку интересно получить максимально возможное значение левой части, можно заменить произведение функций атомного рассеяния fifj на произведение их максимальных значений, равных произведению атомных номеров элементов ZiZj. В этом случае g-2 будет равно единице, и тогда
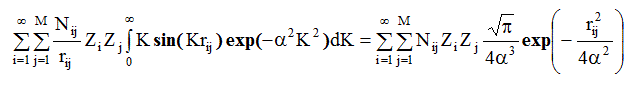
так как 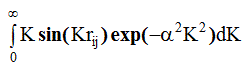 - это табличный интеграл вида
- это табличный интеграл вида 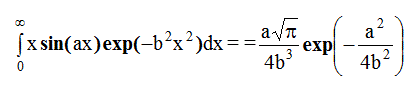 Из соотношения α2K2m = 4, α=2/Km. Тогда
Из соотношения α2K2m = 4, α=2/Km. Тогда
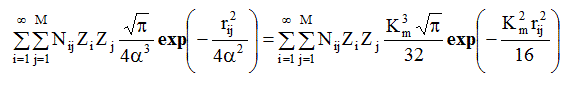 (3.20)
(3.20)
Видно, что в величину двойной суммы в формуле (3.20) вклад вносят только кратчайшие межатомные расстояния, а значит, и ближайшие соседи, то есть суммирование здесь можно ограничить первой координационной сферой. Обозначим
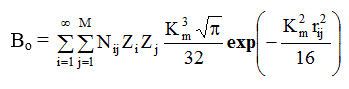
Результаты оценки величины Bo для легких и тяжелых элементов при различных значениях К m приведены в таблице 2.
Таблица 2
Результаты оценки величины Bo для аморфных углерода и тантала
|
Вещество |
Угдерод |
Тантал |
|
R1, Ao N1, ат.
|
1,5 4 73,4 |
3 8 6030 |
|
Km, Ao -3 |
В o, Ao -3 |
В o, Ao -3 |
|
4 7 16 |
54 3 8*10-12 |
60 3 3*10-59 |
Таким образом, наибольшее значение Bo имеет место для легких элементов, имеющих малое значение радиуса первой координационной сферы r1 , когда К m = 4 А o , то есть исследования проведены на СrК α - излучении. Но и в этом случае величина суммы, стоящей в левой части уравнения (3.17), всего лишь сравнима с 2π2poZ , то есть много меньше стоящего в правой части интеграла. Приравнивая левую часть к нулю и подставляя вместо i( К) выражение (2.63), получаем
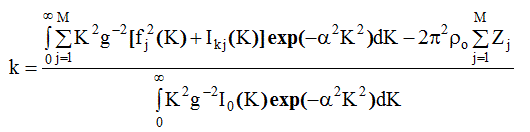 (3.21)
(3.21)
Формула (3.21) отличается от (3.19) домнодением подынтегральных выражений в числителе и знаменателе на exp(- α 2K2), так как g(K ) о бычно выбирают равным f е, а Zj≈Kj,
Кроме изложенных выше трех методов нормировки, можно использовать еще два менее трудоемких. Они основаны на том, что если дальность корреляции в расположении атомов в исследуемом материале или в эталонном веществе невелика, то при больших К интенсивности рассеяния отдельными атомами просто складываются. В первом случае метод нормировки называют нормировкой "по хвосту", а коэффициент нормировки рассчитывают из условия, что прн больших К в каждой точке К i можно приравнять величины :
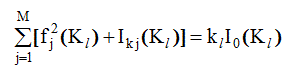 (3.22)
(3.22)
Отсюда
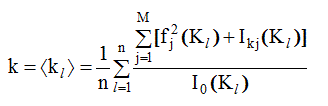 (3.23)
(3.23)
n - число точек, в которых производится расчет коэффициента ki; ![]() - сумма по единице состава, Pi - фактор поляризации , рассчитанный для данного значения К i .
- сумма по единице состава, Pi - фактор поляризации , рассчитанный для данного значения К i .
Во втором случае дальность корреляции в исследуемом материале может быть любой, а в качестве эталона выбирается вещество для которого дальность корреляции невелика. Расчет коэффициента нормировки для эталона k эт производится до формуле (3. 2 3). Для образца
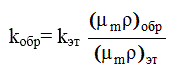 (3.24)
(3.24)
М - молекулярный вес.
Последний метод расчета k широко используется при исследованиях ближнего порядка в кристаллических сплавах [26,271. Эталоном служит плавленный кварц. Однако нужно отметить, что осцилляции на кривой распределения интенсивности рассеяния аморфным SiO2 затухают очень медленно, так как даже для иэлучения С u К α в области К = 7 - 8 Ao -1 (3.22) несправедлива. Точное значение k эт, можно получить, используя для этой цели один из первых трех методов [28 ].