Рентгеноструктурный анализ аморфных материалов
2.5.1. Метод Уоррена
Для выполнения усреднения интенсивности рассеяния I(K) по конфигурациям вво-дится функция fе, физический смысл которой - эффективная амплитуда рассеяния одним электроном материала данного состава. Здесь j- номер атома, М – число атомов в фор-мульной единице исследуемого материала.
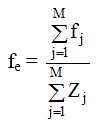 (2.45)
(2.45)
Например, для двуокиси кремния SiO2 М=3: это 1 атом Si и 2 атома 0 , а для сплава состава A0,3B0,7 это 0,3 атома А и 0,7 атома В. Zj - атомный номер j -го атома.
Иными словами, f е - это сумма рассеивающих способностей всех атомов, входящих в единицу состава, деленная на число всех электронов в ней. Далее допускается, что функцию атомного рассеяния любого m - го атома можно считать пропорциональной f е , то есть
fm=Kmfe (2.46)
где Km - постоянная для данного атома величина, близкая по величине к
Zm . К m называют эффективным числом электронов в m -ом атоме и рассчитывают как среднее
значение отношения ![]() , найденного для нескольких значений длины дифракционного вектора K:
, найденного для нескольких значений длины дифракционного вектора K:
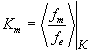 (2.47)
(2.47)
Такое допущение означает, что характер зависимости fm от К одинаков для всех атомов и функции атомного рассеяния различных атомов отличаются друг от друга на постоянный множитель. Это приближение неверно, но, тем не менее, целый ряд полезных результатов получен к настоящему времени именно этим методом.
Формулу (2.44) теперь можно переписать в виде:
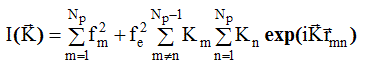 (2.48)
(2.48)
Пусть ![]() - эффективное число электронов в элементе объема dVn находящемся на расстоянии
- эффективное число электронов в элементе объема dVn находящемся на расстоянии ![]() от атома m . Заменяя
от атома m . Заменяя ![]() интегралом по объему образца, перепишем выражение (2.48) в виде:
интегралом по объему образца, перепишем выражение (2.48) в виде:
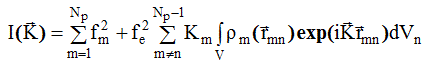 (2.49)
(2.49)
Для того, чтобы интеграл в (2.49) сходился, добавим и вычтем слагаемое, содержащее среднюю электронную плотность r e . Тогда
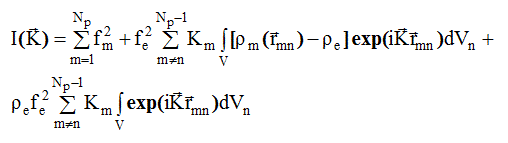
(2.50)
Последнее слагаемое представляет собой интенсивность мало углового рассеяния I мур (K) скоплением из N одинаковых групп, состоящих каждая из n о атомов. Как указывалось в разделе 2.3, I мур (K) обычно имеет заметные значения в области очень малых углов, так что при проведении дальнейших расчетов этой величиной можно пренебречь. Считая, что n о - число атомов в единице состава, а N - число единиц состава в рассеивающем объеме и что все N групп одинаковы, перепишем (2.50) следующим образом
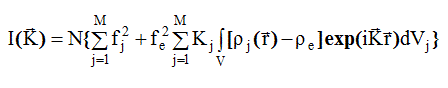 (2.51)
(2.51)
Здесь ![]() среднее значение электронной плотности по всем
среднее значение электронной плотности по всем ![]() в пределах рассеивающего объема образца для расстояния
в пределах рассеивающего объема образца для расстояния ![]() от j -го атома.
от j -го атома.
Для изотропной аморфной системы ![]() , где
, где ![]() , сферически симметрична и стремится к нулю при больших r.
, сферически симметрична и стремится к нулю при больших r.
Приняв за элемент объема dVj , объем сферического слоя, заключенного между сферами радиуса r и r+dr (dVj=4 p r2dr), и учитывая, что вероятность того, что вектор ![]() составляет с вектором
составляет с вектором ![]() угол a , равна
угол a , равна ![]() , запишем для среднего значения интенсивности рассеяния
, запишем для среднего значения интенсивности рассеяния ![]() следующее выражение :
следующее выражение :
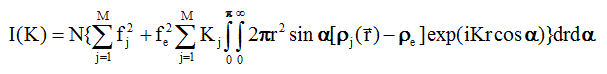 (2.52)
(2.52)
Интегрируя по a , получим
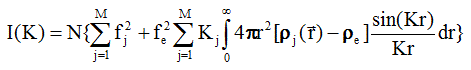 (2.53)
(2.53)
Величина 4 p r2 r j(r)dr - это число электронов в сферическом слое толщиной dr , находящемся на расстоянии r от j- го атома. Введем обозначение :
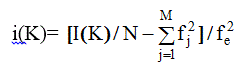 (2.54)
(2.54)
Функция i(K) представляет собой интерференционную функцию рассеяния многокомпо-нентной системой атомов.
и перепишем формулу (2.53) следующим образом :
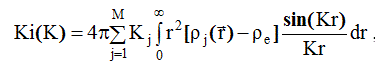 (2.55)
(2.55)
Фурье - преобразование дает:
 (2.56)
(2.56)
На рис. 7 приведены кривые распределения: интенсивности рассеяния (рис.7а); функции Кj(К) (рис.7б) и
функции 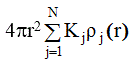 для аморфного SiO2 (риc.7в) [8, 13]. В верхней части рис.7в указаны значения радиусов
координационных сфер для кристаллического кварца SiO2. Видно, что положения пиков на кривой
для аморфного SiO2 (риc.7в) [8, 13]. В верхней части рис.7в указаны значения радиусов
координационных сфер для кристаллического кварца SiO2. Видно, что положения пиков на кривой 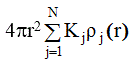 отвечают расстояниям Si - O; O - O; Si - Si. Число атомов на данном расстоянии от атома, принятого
за начальный, рассчитывается из площади под соответствующими пиками на кривой
отвечают расстояниям Si - O; O - O; Si - Si. Число атомов на данном расстоянии от атома, принятого
за начальный, рассчитывается из площади под соответствующими пиками на кривой 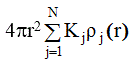 . Первый пик на кривой
. Первый пик на кривой 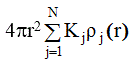 для аморфного SiO2 имеет место при значении расстояния r=1.62 Å (рис.7в), что соответствует кратчайшему расстоянию
(сумме атомных радиусов) между атомами кремния и кислорода (Si и О). Поскольку при суммировании по формульной
единице за начальный поочередно принимается каждый из двух атомов кислорода и атом кремния, то ясно, что первый максимум
является суперпозицией трех пиков: один обусловлен ближайшими кислородными соседями вокруг кремния NSi-O и два -
ближайшими кремниевыми соседями вокруг первого и второго атомов кислорода NO-Si: NSi-O и NO-Si - координационные числа
для кремния и кислорода соответ-ственно. Пусть S1 - площадь под первым максимумом, тогда, исходя из вышесказанного:
для аморфного SiO2 имеет место при значении расстояния r=1.62 Å (рис.7в), что соответствует кратчайшему расстоянию
(сумме атомных радиусов) между атомами кремния и кислорода (Si и О). Поскольку при суммировании по формульной
единице за начальный поочередно принимается каждый из двух атомов кислорода и атом кремния, то ясно, что первый максимум
является суперпозицией трех пиков: один обусловлен ближайшими кислородными соседями вокруг кремния NSi-O и два -
ближайшими кремниевыми соседями вокруг первого и второго атомов кислорода NO-Si: NSi-O и NO-Si - координационные числа
для кремния и кислорода соответ-ственно. Пусть S1 - площадь под первым максимумом, тогда, исходя из вышесказанного:
S1=KSi NSi-O KO+2 KO NO-Si KSi (2.57)
При стехиометрическом составе NO-Si= NSi-O/2, тогда S1=2KSiNSi-OKO, откуда первое координационное число NSi-O для кремния Si равно:
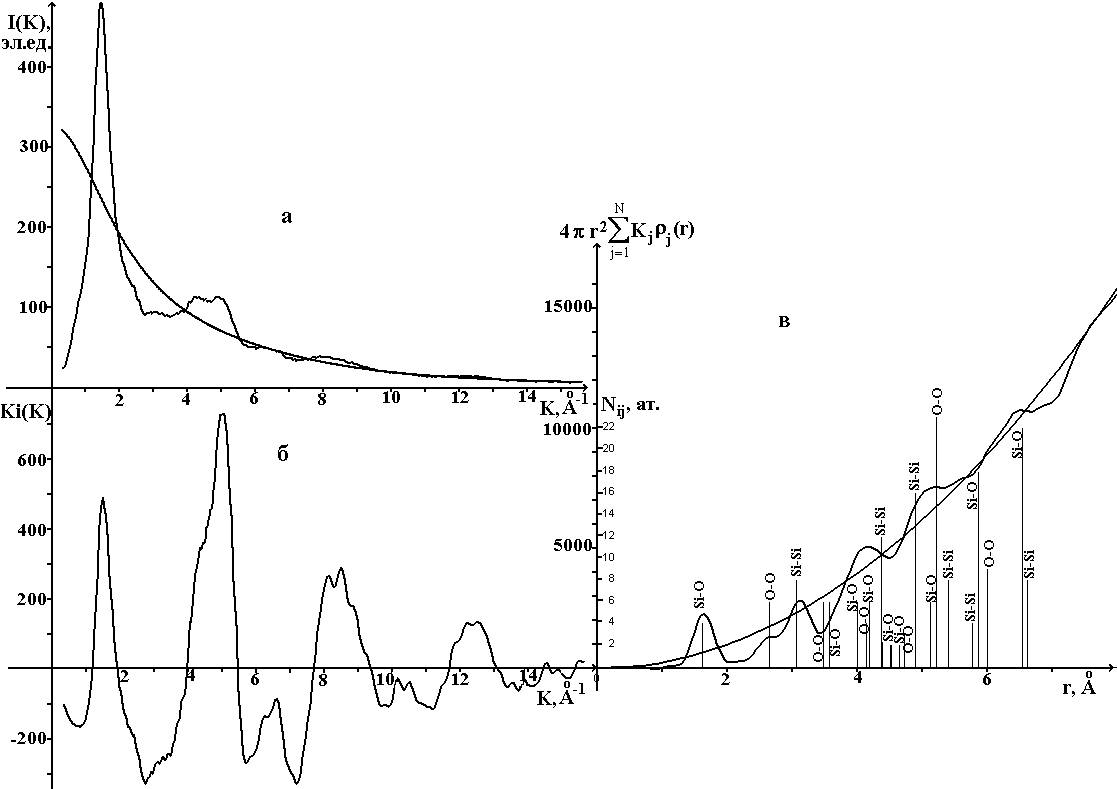
Ри c .7. Кривые распределения: Риc. 7. Кривая распределения интенсивности рассеяния, полученная для плавленого кварца на излучении МоKα (а), и рассчитанные из нее: б – K-взвешенная интерференци-онная функция (б), функция радиального распределения электронной плотности (в). Штрихами показаны радиусы координационных сфер.