Рентгеноструктурный анализ аморфных материалов
1.1 Ближний порядок в расположении атомов
Неупорядоченным, некристаллическим, аморфный называют материал, в котором отсутствует трансляционная симметрия в расположении составляющих его частиц: атомов, ионов, молекул. Однако это не означает, что в неупорядоченных веществах имеет место полный, абсолютный беспорядок. Даже в газах, наиболее беспорядочных из всех имеющихся объектов, существует какой-то порядок, поскольку ни одна из составляющих их частиц не может приблизиться к другой на расстояние, меньшее суммы их радиусов: тот факт, что одна частица занимает определенную область пространства, обуславливает запрещенность этого участка для другой.
Таким образом, ни одно скопление частиц не может быть полностью беспорядочным, поскольку для любой частицы этого скопления не все положения в пространстве равновероятны.
Конечность размеров частиц, образующих данный некристаллический материал, - причина возникновения простейшего порядка, заключающегося в том, что какие-то расстояния между частицами встречаются чаще, чем другие.
Порядок в расположении частиц, имеющий место в газах, жидкостях и аморфных твердых телах и распространяющийся на расстояния, отвечающие нескольким межатомным (межмолекулярным) расстояниям, называют ближним порядком, или дистанционным ближним порядком.
Можно сказать, что в некристаллических материалах отсутствует дальний порядок, но сохраняется в пределах нескольких межчастичных расстояний ближний порядок. Размер области ближнего упорядочения обуславливается характером и величиной сил межчастичного взаимодействия. В многокомпонентных некристаллических системах (то есть в системах, состоящих из различных частиц), наряду с дистанционным, может иметь место и сортовой (композиционный или химический) ближний порядок, обусловленный стремлением частиц одного сорта окружать себя частицами либо того же, либо иного сорта.
Наиболее сложен ближний порядок в веществах, в которых каждая частица представляет собой молекулу. Здесь различают два типа порядка: внутри- и межмолекулярный. Первый обусловлен характером расположения атомов внутри молекулы, второй - порядком в расположении самих молекул.
Ближний порядок в некристаллических материалах характеризуют кривой W(r), каждая точка которой представляет собой плотность вероятности существования в системе пары частиц, находящихся на расстоянии r друг от друга.
Рассмотрим физический смысл функции W(r).
Пусть система, состоящая из N частиц, занимает объем V, а малые элементы объема dV1 и dV2 зафиксированы с помощью радиус-векторов ![]() и
и ![]() (рис.1), проведенных из некоторого начала координат 0. Если частицы расположены хаотически,то вероятность нахождения одной из них в объеме dV1, а другой в объеме dV2 в силу независимости их положений равна
(рис.1), проведенных из некоторого начала координат 0. Если частицы расположены хаотически,то вероятность нахождения одной из них в объеме dV1, а другой в объеме dV2 в силу независимости их положений равна
![]() (1.1)
(1.1)
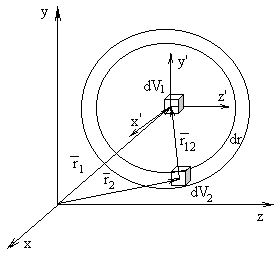
Рис.1. Взаимное расположение частиц в объемах
Хаотическое расположение частиц возможно лишь в идеальном газе, когда собственные объемы частиц и силы взаимодействия между ними можно не принимать во внимание. В реальных материалах частицы не могут находиться на произвольном расстоянии друг от друга хотя бы потому, что их упаковка достаточно плотная.>Это означает, что нахождение некоторой частицы в какой-либо точке объема V зависит от того, где при этом находятся другая. Такая вероятностная связь между взаимным расположением частиц называется корреляцией и описывается количественно с помощью функции W(![]() ,
, ![]() ), которая в общем случае зависит от шести координат рассматриваемой пары частиц.
), которая в общем случае зависит от шести координат рассматриваемой пары частиц.
Необходимо отметить, что функция W(![]() ,
,![]() ), характеризует расположение частиц в любом веществе: как в кристаллическом, так и в некристаллическом. В случае однородной и изотропной среды, к какой относятся газы, жидкости и аморфные твердые тела, функция W зависит только от скалярного значения расстояния между атомами
), характеризует расположение частиц в любом веществе: как в кристаллическом, так и в некристаллическом. В случае однородной и изотропной среды, к какой относятся газы, жидкости и аморфные твердые тела, функция W зависит только от скалярного значения расстояния между атомами ![]() .
.
W(![]() ) = W(r). (1.2)
) = W(r). (1.2)
где ![]() =
= ![]() –
– ![]()
Функция W(г) называется радиальной функцией распределения. Выражение (1.1) теперь можно записать как
![]() , (1.3)
, (1.3)
где dp(r)- вероятность одновременного нахождения одного атома в объеме dV1, а другого в объеме dV2 на расстоянии r друг от друга.
Радиальная функция распределения W(r)- величина безразмерная
Равенство (1.3) можно представить в ином виде. Для этого перенесем начало координат в центр элементарного объема, в котором находится первый атом. Вероятность нахождения второго атома в объеме dV2:
![]()
Интегрирование по объему означает, что начало координат помещается последовательно в каждую частицу объема V.Для однородной изотропной среды dp’(![]() )= dp’(r); W(
)= dp’(r); W(![]() ) = W(r), тогда
) = W(r), тогда
![]()
Если теперь за dV2 принять объем, заключенный между двумя сферами, имеющими радиусы r и r + dr и центр в начале координат, то
![]() (1.4)
(1.4)
так как объем dV2 сферического слоя толщиной dr
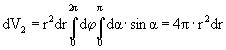
Условие нормировки функции W(r)
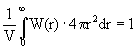 (1.5)
(1.5)
означает, что сумма вероятностей обнаружения частицы на каком-либо из всех возможных расстояний от частицы, принятой за начальную, равна 1.
Если в указанном i слое находится dNi частиц, тоих число в единице объема этого слоя можно найти по формуле:
![]() (1.6)
(1.6)
В различных сферических слоях число атомов различно, поэтому r i является функцией от ri. В аморфных материалах r i (ri) является непрерывной функцией от r и величина 4p r (r)r2dr определяет число частиц в сферическом слое, заключенном между сферами радиусов r иr + dr. Функцию r (r) называют радиальной функцией распределения атомной плотности (РФР). r (r) нормируется условием
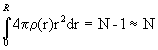 (1.7)
(1.7)
Объем интегрирования V - сфера радиуса R в неограниченной однородной среде. Объем ее должен быть достаточно велик (N>>1), а частицы, расположенные вблизи поверхности сферы, имеют то же окружение, что и частицы в центре. Если материал неоднороден, то есть N флуктуирует около какого-то среднего значения < N> при переходе от одной сферы радиуса R к другой (в частности, вследствие теплового движения такие флуктуации имеют место в газах и жидкостях), то формула (1.7) принимает вид:
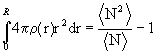 (1.8)
(1.8)
Сопоставляя (1.5) и (1.7), находим связь междуW(r) и r (r).
![]() (1.9)
(1.9)
где p0 - средняя плотность частиц материала.p0 можно рассчитать, зная плотность p’ и молекулярный вес (М.В.) исследуемого вещества.
![]() (1.10)
(1.10)
где mс = 1/12 массы атома углерода.
В свою очередь, ФРР электронной плотности pe(r) связана с W(r):
pe(r) = W(r) peo (1.11)
где peo - средняя электронная плотность вещества.
![]() (1.12)
(1.12)
где Zj - атомный номер j - го элемента, m – число атомов в частице или в формульной единице соединения.
Функции W(r), r (r), r e(r ) являются важнейшими и основными характеристиками реальных газов, жидкостей и аморфных тел.