Элементы рентгеноструктурного анализа
Аномалии фактора атомного рассеяния: эффект дисперсии.
Выражения для функции атомного рассеяния, записанные выше, применимы только в тех случаях, когда частота падающего излучения велика по сравнению с частотой К-скачка поглощения рассеивающего атома. Если принять классическую модель атома, то можно заранее сказать, что при приближении частоты к критическому значению возникнет явление резонанса и колебания, возбужденные в атоме падающей волной, будут модулированы так же, как и рассеянное излучение. Длины волн, используемые в структурном анализе, близки к скачкам поглощения часто встречающихся элементов, и потому в ряде случаев необходимо учитывать явление “аномальной дисперсии”. Квантовую теорию явления разработал Хёнль. Была предпринята попытка экспериментальной проверки теории, но необходимые для этого прецизионные измерения интенсивности дифракции все же не удалось сделать с достаточной точностью.
При отсутствии надежных экспериментальных результатов в тех случаях, когда это нужно для целей рентгеноструктурного анализа, лучше пользоваться результатами теоретических расчетов. Мы приведем здесь без доказательств те окончательные выводы, которые могут оказаться полезными.
Фактор атомного рассеяния принимается равным (когерентное рассеяние)
f = f1- Δ f.
1) Если рассеивающий объект и длина волны заданы, то Δ f не зависит от угла рассеяния. Если К-скачок поглощения рассеивающего объекта соответствует λк, то Δ f является функцией отношения λ/ λк, мало зависящей от природы рассеивающего атома.
Кривые рис. 1 дают возможность рассчитать поправку для Si, Fe, W;
для остальных атомов достаточна интерполяция. При λ>λк поправка Δ f равна величине а, определяемой по кривой а рис. 1. При λ < λк нужно к величине а прибавить дополнительно b/(f+a), причем значение b определяется по кривой b рис. 1б.
2) Если λ велика по сравнению с λк , то a стремится к постоянному значению, заключенному в интервале от -1 до -1,5. Эти величины показывают, что поправка существенна и ею нельзя пренебрегать, даже когда мы не находимся в области, где фактор f1 резко аномален.
3) Скачок L соответствует большой длине волны и совсем не играет роли при таких сравнительно коротких длинах волн, как Мо Кa. При излучении Сu Кa он мог бы играть роль для элементов, более тяжелых, чем редкоземельные. Таких таблиц для соответствующего расчета не составлено.
Аномалия фактора атомного рассеяния находит следующее интересное применение. Если изучается кристалл, образованный двумя элементами с последовательными атомными номерами, например Сu и Zn, то их факторы
рассеяния f почти во всем интервале sinθ/λ весьма близки, и при помощи рентгеновских лучей эти атомы невозможно различить. Для sinθ/λ = 0,3. таблицы дают f(Cu)=17.8 и f(Zn)=18,2 но если использовать излучение Cu Kβ
с длиной волны, равной 1,392 А, то отношения λ/ λк для Сu н Zn становятся соответственно равными 1,0085 и 1,08. При помощи кривых рис. 1 находим Δf(Cu)=-5,2 и Δf(Zn)=-2,8 отсюда имеем f1(Cu)= 12,6 и f1 (Zn)= 15,4.
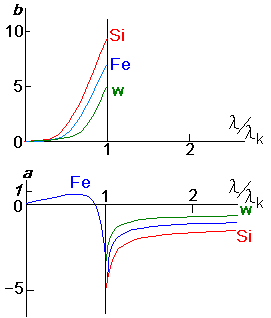
Рис1 Кривые для определения элементов фактора атомного рассеяния вблизи скачка поглощения λк >
Различие между двумя сортами атомов значительно возросло. В расчетах структуры CuZn фигурирует величина [{f(Cu)- f(Zn)}/{ f(Cu)+ f(Zn)}]2 которая при излучении с произвольной длиной волны, например Мо Ка, имеет значение 0,05%, но для Сu Кa. возрастает до 4%. Возможность использования такого приема необходимо всегда иметь в виду при изучении структуры сплавов, образованных металлами, являющимися соседями в периодической таблице
4) Отметим еще одно следствие, вытекающее из явления дисперсии. При рассеянии волны на атоме фаза меняется на π, но поскольку это изменение одинаково для всех атомов, то его можно не учитывать при расчете интерференции.
Однако когда длина волны близка к скачку поглощения, изменение отличается от π. Если амплитуда рассеянного излучения всегда равна амплитуде падающего излучения, умноженной на f, то фактор рассеяния оказывается комплексным числом, модулем которого является отношение амплитуд, а аргументом — разница фаз.